Icositetrágono
En geometría, un icositetrágono (o icosikaitetrágono) o 24-gono es un polígono de veinticuatro lados. La suma de los ángulos interiores de cualquier icositetrágono es de 3960 grados.
| Icositetrágono | ||
|---|---|---|
 Un icositetrágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 24 | |
| Vértices | 24 | |
| Grupo de simetría | , orden 2x24 | |
| Símbolo de Schläfli | {24}, t{12}, tt{6}, ttt{3} (icositetrágono regular) | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área |
(lado ) | |
| Ángulo interior | 165° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Icositetrágono regular
El icositetrágono regular está representado por el símbolo de Schläfli {24} y también se puede construir como un dodecágono truncado, t{12}, o un hexágono truncado dos veces, tt{6}, o un triángulo truncado tres veces, ttt{3}.
Un ángulo interior en un icositetrágono regular es de 165°, lo que significa que un ángulo exterior sería de 15° (véase número trigonométrico).
El área de un icositetrágono regular es: (con a = longitud del lado)
El icositetrágono forma parte de la secuencia de polígonos regulares de aproximación al número π utilizada por Arquímedes, junto con el hexágono (6-gono), el dodecágono (12-gono), el tetracontaoctágono (48-gono) y el eneacontahexágono (96-gono).
Construcción
Como 24 = 23 × 3, un icositetrágono regular es construible usando una trisección del ángulo.[1] Como un dodecágono truncado, puede construirse mediante la bisección de los lados de un dodecágono regular.
Simetría
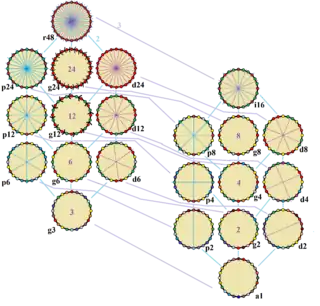
El icositetrágono regular tiene simetría Dih24, de orden 48. Hay 7 simetrías diédricas de subgrupos: (Dih12, Dih6, Dih3) y (Dih8, Dih4, Dih2 Dih1), y 8 simetrías cíclicas: (Z24, Z12, Z6, Z3) y (Z8, Z4, Z2, Z1).
Estas 16 simetrías básicas se pueden ver en 22 simetrías distintas en el icositetrágono. John Conway las etiqueta por orden de letras y grupos.[2] La simetría completa de la forma regular es r48 y ninguna simetría está etiquetada como a1. Las simetrías diédricas se dividen en función de si pasan por vértices (d para diagonales) o aristas (p para perpendiculares), e i cuando las líneas de reflexión pasan por un vértice y por el centro de un arista. Las simetrías cíclicas en la columna del medio están etiquetadas como g con sus órdenes de giro central.
Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Solo el subgrupo g24 no tiene grados de libertad (los vértices deben estar distribuidos necesariamente como en el polígono regular), por lo que puede verse como un grafo dirigido.
Disección
 regular |
 Isotoxal |
Harold Scott MacDonald Coxeter establece que todo zonágono (un polígono de 2m lados, cuyos lados opuestos son paralelos y de igual longitud) se puede dividir en m(m-1)/2 paralelogramos.[3] En particular, esto es cierto para polígonos regulares con muchos lados iguales, en cuyo caso los paralelogramos son todos rombos. Para el icositetrágono regular, m=12, y se puede dividir en 66: 6 cuadrados y 5 conjuntos de 12 rombos. Esta descomposición se basa en el polígono de Petrie proyección de un hipercubo.
 |
 |
 |
 |
Polígonos relacionados
Un icositetragrama es un estrella de 24 lados. Hay 3 formas regulares proporcionadas por los símbolos de Schläfli: {24/5}, {24/7} y {24/11}. También hay 7 figuras de estrellas regulares que usan la misma disposición de vértices: 2{12}, 3{8}, 4{6}, 6{4}, 8{3}, 3{8/3} y 2{12/5}.
| Icositetragramas como polígonos estrellados y figuras estrelladas | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Forma | Polígono convexo | Compuestos | Polígono estrellado | Compuesto | |||||||
| Image |  {24/1}={24} |
.svg.png.webp) {24/2}=2{12} |
.svg.png.webp) {24/3}=3{8} |
.svg.png.webp) {24/4}=4{6} |
 {24/5} |
.svg.png.webp) {24/6}=6{4} | |||||
| Ángulo interior | 165° | 150° | 135° | 120° | 105° | 90° | |||||
| Forma | Polígono estrellado | Compuestos | Polígono estrellado | Compuesto | |||||||
| Imagen |  {24/7} |
.svg.png.webp) {24/8}=8{3} |
.svg.png.webp) {24/9}=3{8/3} |
.svg.png.webp) {24/10}=2{12/5} |
 {24/11} |
.svg.png.webp) {24/12}=12{2} | |||||
| Ángulo interior | 75° | 60° | 45° | 30° | 15° | 0° | |||||
También hay icositetragramas isogonales construidos como truncamientos más profundos del dodecágono {12} y del dodecagrama {12/5} regulares. Estos también generan dos cuasitruncamientos: t{12/11}={24/11} y t{12/7}={24/7}.[4]
| Truncamientos isogonales de dodecágono y dodecagrama regulares | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cuasiregular | Isogonal | Cuasiregular | |||||||||
 t{12}={24} |
 |
 |
 |
 |
 |
 t{12/11}={24/11} | |||||
 t{12/5}={24/5} |
 |
 |
 |
 |
 |
 t{12/7}={24/7} | |||||
Icositetrágono oblicuo
| {12}#{ } | {12/5}#{ } | {12/7}#{ } |
|---|---|---|
 |
 |
 |
| Las aristas en zigzag de un antiprisma dodecagonal, de un antiprisma dodecagrámico o de un antiprisma dodecagrámico cruzado, forman un icositetrágono oblicuo regular | ||
Un icositetrágono oblicuo es un polígono alabeado con 24 vértices y aristas pero que no se hallan en el mismo plano. El interior de tal icositetrágono generalmente no está definido. Un icositetrágono en zig-zag oblicuo tiene vértices que se alternan entre dos planos paralelos.
Un icositetrágono oblicuo regular es una figura isogonal con longitudes de arista iguales. En 3 dimensiones será un icositetrágono oblicuo en zig-zag y se puede ver en los vértices y aristas laterales de un antiprisma dodecagonal con la misma simetría D12d, [2+,24], orden 48. El antiprisma dodecagrámico, s{2, 24/5} y el antiprisma cruzado dodecagrámico, s{2,24/7} también tienen dodecágonos oblicuos regulares asociados.
Polígonos de Petrie
El icositetrágono regular es el polígono de Petrie para muchos politopos de dimensiones superiores, vistos como proyecciones en el plano de Coxeter, que incluyen:
| 2F4 | ||
|---|---|---|
 24-celdas bitruncado |
 24-celdas runcinado |
 24-celdas omnitruncado |
| E8 | ||
|---|---|---|
 421 |
 241 |
 142 |
Referencias
- Constructible Polygon
- John Horton Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- Harold Scott MacDonald Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Enlaces externos
- Weisstein, Eric W. «Icositetragon». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Nombrando polígonos y poliedros
- (simple) polígono
- icosatetragon