Variedad (matemáticas)

Cuando nos desplazamos por la esfera terrestre nos orientamos utilizando mapas planos reunidos en un atlas. En el límite de cada mapa figura la información necesaria para «pegar» mentalmente el mapa siguiente. Para poder hacerlo, es necesaria una cierta redundancia en la información: así, tanto el mapa de Europa como el de Asia pueden contener Moscú. De un modo similar, en matemática es posible describir una variedad utilizando una colección de «mapas» o «cartas» reunidos en un «atlas» e indicando cómo pasar de un mapa a otro. El globo terrestre es un ejemplo típico de variedad, pues puede ser representado por una colección de mapas geográficos.

Un mapa es una porción de la variedad análoga a un espacio vectorial; los cambios de mapa indican cómo estas porciones de variedades se acoplan entre sí. Así, para describir un círculo es posible tomar como mapas dos arcos superpuestos.

En general no es posible describir una variedad a partir de un solo mapa, pues la estructura global de la variedad es diferente de la estructura simple del espacio modelo. Por ejemplo, ningún mapa plano puede describir convenientemente toda la Tierra. Las variedades aparecen como espacios topológicos y sus topologías sólo están determinadas por la situación de sus respectivos mapas.

Una variedad n-dimensional M es un conjunto dotado de una colección P de «cartas abstractas» (funciones uno a uno x de D en M, donde D es un conjunto abierto de un espacio euclídeo de n dimensiones, E(n)) tal que

1) M está cubierta por las imágenes de las cartas de la colección P.

2) Para dos cartas cualesquiera x, y de la colección P, las funciones y^-1x y x^-1y son euclídeamente diferenciables (y están definidas en conjuntos abiertos de E(n) ).

Por lo tanto una superficie es lo mismo que una variedad bidimensional. El espacio euclídeo E(n) es una variedad n-dimensional muy especial ya que su colección de cartas consiste solamente en la función identidad.[1]

Figura 2. Ejemplos de curvas : ■ círculos, ■ parábolas, ■ hipérbolas, ■ cúbicas.

La primera noción relacionada con la variedad es su dimensión. La dimensión designa el número de parámetros independientes que es necesario fijar para situar localmente a un punto sobre la variedad.

• Las curvas son variedades de dimensión uno.
• En una superficie, son necesarias dos coordenadas. Sobre la esfera terrestre, por ejemplo, será necesario precisar la latitud y la longitud.
• Existen numerosas variedades de dimensión superior a dos. Estas variedades son representables gráficamente de manera compleja, para ello, por ejemplo se usan diagramas de Heegaard o diagramas Freedman-Kirby.

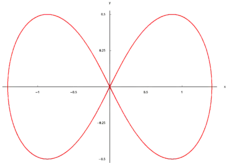
Todas las variedades con una misma dimensión n — o n-variedades — tienen la misma topología local. Así, una pequeña porción de la curva es análoga a una recta y una pequeña porción de superficie es análoga a un plano. No obstante, las variedades se distinguen por su aspecto global. Por ejemplo, en la figura 2 la variedad roja está formada por dos círculos, y resulta visiblemente imposible deformarla de manera continua para obtener una de las otras tres curvas. Del mismo modo, una esfera y un toro no se parecen topológicamente. En general, la topología global puede complicarse por la presencia de agujeros, asas, etc.

Figura 4. Botella de Klein.

Existen numerosos subconjuntos del espacio tridimensional que pueden tener una estructura de variedades: el círculo, el cilindro, la esfera, la cinta de Möbius etc. Estos subconjuntos se denominan subvariedades.

Existen también las denominadas variedades abstractas, como la botella de Klein representada en la figura 4. La botella de Klein puede ser descrita por un sistema de mapas y coordenadas representado por la red de meridianos y paralelos de la figura.

El teorema de inmersión de Whitney muestra que toda variedad abstracta de dimensión n puede realizarse como subvariedad de un espacio de dimensión suficientemente grande (2n). Así, la botella de Klein no puede representarse en el espacio de tres dimensiones, pero forma una subvariedad del espacio de cuatro dimensiones.

En 1851 Bernhard Riemann ofreció la primera definición de variedad, a la que denominó Mannigfaltigkeit'

Véase también: Historia de la Geometría

Bernhard Riemann fue el primer matemático que extendió sistemáticamente la noción de superficie a los objetos de mayores dimensiones, a los que llamó Mannigfaltigkeit.[2] De este vocablo procede el inglés manifold. Riemann ofrece una descripción intuitiva de variedad, considerando una variedad de dimensión n como un «apilamiento» continuo de variedades de dimensión n-1. En la acepción moderna de variedad, esta descripción intuitiva sólo es válida localmente, es decir, en el entorno de cada punto de la variedad. Riemann utiliza este concepto para describir el conjunto de valores de una variable sometida a ciertas restricciones, como el conjunto de los parámetros que describen la posición de una figura en el espacio.

A partir de entonces, las variedades empiezan a aplicarse en numerosos dominios. En matemática, se aplican al estudio de la prolongación analítica y de las variedades abelianas en análisis complejo y al estudio de los flots diferenciables con la aplicación de premier retour de Poincaré. En física, las variedades se aplican a la definición de las mecánicas hamiltoniana y lagrangiana. En 1904, al estudiar las variedades de dimensión 3, Henri Poincaré descubre uno de los problemas más célebres de la teoría de las variedades, la conjetura de Poincaré, demostrada por Grigori Perelmán y validada en junio de 2006.

A pesar de su popularidad, la noción de variedad siguió siendo borrosa. En 1912 Hermann Weyl ofreció una descripción intrínseca de las variedades diferenciables.[3] Las publicaciones de los años 30, con ocasión de la prueba del teorema de inmersión por Hassler Whitney, dejaron bien establecido el concepto.

Localmente, la circunferencia parece una línea, que tiene una sola dimensión. En otros términos, una sola coordenada es suficiente para describir un pequeño arco de circunferencia. Consideremos, por ejemplo, la parte superior de la circunferencia, para la que la coordenada y es positiva (la parte amarilla en la figura 1). Cualquier punto de esta parte puede ser descrito por la coordenada x. Existe, por lo tanto, un homeomorfismo χ_arribaentre la parte amarilla de la circunferencia y el intervalo abierto [−1, 1] que representa cada punto de la circunferencia por su primera coordenada:

${\displaystyle \chi _{\mathrm {arriba} }(x,y)=x.\,}$

A tal función se le denomina un mapa o carta. Del mismo modo, existen mapas para las partes inferiores (rojo), izquierda (azul) y derecha (verde) de la circunferencia. Juntas, todas ellas recubren la totalidad de la circunferencia y decimos que los cuatro mapas conforman un atlas de esa circunferencia.

Los dos mapas superior e izquierdo se superponen. Su intersección se sitúa en el cuarto de circunferencia donde las coordenadas x e y son, respectivamente, negativa y positiva. El mapa χ_arriba realiza una biyección que en (x,y) asocia x, partiendo de la zona de superposición hacia el intervalo [-1,0]. El mapa χ_izquierda por el que (x,y) da y asocia a esta misma zona de superposición el intervalo [0,1]. De este modo, es posible crear una función T del intervalo [-1,0] hacia [0,1]:

${\displaystyle T_{\mathrm {arriba} \rightarrow \mathrm {izquierda} }(x)=\chi _{\mathrm {izquierda} }\left(\chi _{\mathrm {arriba} }^{-1}(x)\right)=\chi _{\mathrm {izquierda} }\left(x,{\sqrt {1-x^{2}}}\right)={\sqrt {1-x^{2}}}.}$

Tal función se llama aplicación de cambio de mapa, de cambio de cartas o simplemente de transición. Permite pasar del sistema de coordenadas x elegido para el primer mapa al sistema de coordenadas y elegido para el segundo.

La aplicación pendiente forma un mapa que describe todos los puntos de la circunferencia excepto uno.

Los mapas superior, inferior, derecho e izquierdo muestran que la circunferencia es una variedad, pero no conforman el único atlas posible. Los mapas no tienen por qué ser proyecciones geométricas y su número es prácticamente arbitrario.

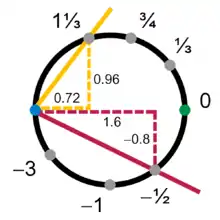
He aquí otro ejemplo de descripción de una circunferencia. Si tomamos como punto de base el punto de coordenadas (-1, 0) y trazamos diferentes rectas desde ese punto; la recta derecha de pendiente s corta a la circunferencia en un punto único. La correspondencia entre la pendiente de la derecha y las coordenadas de un punto de intersección es en un sentido:

${\displaystyle \chi _{\mathrm {menos} }(x,y)=s={y \over {1+x}}}$ ;

y en el otro:

${\displaystyle x={{1-s^{2}} \over {1+s^{2}}},\qquad y={{2s} \over {1+s^{2}}};}$.

Este primer mapa describe todos los puntos de la circunferencia excepto el punto de base.

Para construir el segundo mapa hacemos una simetría tomando como punto de base (+1, 0) y como pendiente t con:

${\displaystyle \chi _{\mathrm {mas} }(x,y)=t={y \over {1-x}}}$.

Estos dos mapas proporcionan un segundo atlas de la circunferencia, teniendo por aplicación de cambio de mapa

${\displaystyle t={-1 \over s}=\varphi (s)}$.

Cada mapa omite un solo punto, sea (−1,0) para s o (+1,0) para t, de modo que ningún mapa solo puede describir completamente la circunferencia.

Hemos visto que los dos atlas presentados son compatibles, es decir, que agrupando los cuatro mapas del primero y los dos del segundo, obtenemos un nuevo atlas, todavía más redundante. Cada uno de ellos, así como el atlas global, definen la misma noción de orientación (repérage) por mapa y coordenadas locales, es decir, la misma estructura de variedad. Más adelante, se mostrará cómo el resultado de la ecuación ${\displaystyle x^{2}+y^{2}=1}$ permite también crear sistemas de mapas locales adaptados.

A partir de estos ejemplos, podemos comprobar la flexibilidad que nos permite la utilización de mapas: disponemos de una variedad infinita de atlas compatibles sobre la circunferencia. Nuestra elección dependerá de la geometría del problema estudiado. Sin embargo, podemos demostrar topológicamente que un solo mapa no podrá jamás cubrir la totalidad de la circunferencia.

Las variedades más sencillas de definir son las variedades topológicas, pues se parecen localmente a un espacio euclídeo ordinario Rⁿ. Formalmente, una variedad topológica es un espacio topológico en que cada punto tiene un entorno homeomorfo a un abierto de Rⁿ. Estos homeomorfismos son las cartas o mapas de la variedad.

Una esfera, ejemplo de variedad diferenciable.

Las variedades diferenciables conforman una subclase especial de las variedades topológicas. Si las cartas locales en una variedad son aplicaciones diferenciables en el espacio de coordenadas, entonces podemos definir funciones diferenciables en esa variedad y un espacio tangente en cada punto. En particular, es posible utilizar el cálculo en una variedad diferenciable. La esfera bidimensional es un ejemplo clásico de variedad diferenciable.

En la geometría de Riemann, una variedad de Riemann es una variedad diferenciable real en la cual cada espacio tangente se equipa con un producto interno de manera que varíe suavemente de punto a punto. Esto permite que se definan varias nociones métricas como longitud de curvas, ángulos, áreas (o volúmenes), curvatura, gradiente de funciones y divergencia de campos vectoriales.

Informalmente, un grupo de Lie es un grupo continuo, es decir, un grupo en el que tanto sus elementos como la operación varían continuamente. Un ejemplo típico es el grupo de rotaciones del plano alrededor de un punto. Esta idea se usa en contraposición a la de grupo «abstracto» o «algebraico», en cuyo estudio priman más los aspectos operacionales que los geométricos.

Por ejemplo, el espacio euclídeo ${\displaystyle \mathbb {R} ^{n}}$ con la operación de adición de vectores, o el conjunto de matrices reales nxn con determinante 1 son grupos de Lie. El primero se interpreta geométricamente como un grupo traslaciones; el segundo, transformaciones lineales que conservan el volumen.

Formalmente, un grupo de Lie ${\displaystyle G}$ es una variedad diferenciable real o compleja provista de una estructura de grupo, debiendo ser las operaciones sobre tal grupo igualmente diferenciables u holomorfas.

• Una variedad compleja es una variedad modelada sobre Cⁿ con funciones de transición holomorfas. Estas variedades son los objetos básicos de estudio en geometría compleja. Una variedad compleja de dimensión compleja uno se llama superficie de Riemann. Notemos que una variedad compleja de dimensión n tendrá dimensión 2n considerada como variedad diferenciable real.
• Variedades de dimensión infinita: para permitir el uso de dimensión infinita podemos considerar las variedades de Banach, que son localmente homeomorfas a un espacio de Banach. Otra posibilidad son las variedades de Fréchet, localmente homeomorfas a espacios de Fréchet.
• Una variedad simpléctica es una clase de variedad usada para representar los espacios de fases en Mecánica Clásica. Para ello, están dotadas con una 2-forma que permite definir el corchete de Poisson. Muy relacionadas con este tipo de variedades están las variedades de contacto.
• Una variedad compacta es una variedad tal que de todo recubrimiento abierto se puede extraer un subrecubrimiento finito. Aunque esta definición es perfectamente aplicable a variedades topológicas, se suele entender que una variedad compacta es además una variedad diferenciable. De manera informal, una variedad compacta es la generalización a variedades de dimensión cualquiera de los conceptos de curva cerrada y de superficie cerrada.
• En una variedad con borde D, cada punto admite un entorno homeomorfo o bien a un abierto de ${\displaystyle \mathbb {R} ^{n+1}}$ (puntos interiores, que forman la variedad ${\displaystyle \operatorname {Int} D}$ de dimensión ${\displaystyle n+1}$) o bien a uno de ${\displaystyle \mathbb {R} ^{n}\times [0,+\infty )}$ que contiene al origen (puntos del borde, que forman la variedad ${\displaystyle n}$-dimensional ${\displaystyle \partial D}$). Por el teorema de invarianza del dominio, los conjuntos ${\displaystyle \operatorname {Int} D}$ y ${\displaystyle \partial D}$ son disjuntos. A menudo se exige diferenciabilidad o que D sea un subconjunto cerrado de otra variedad (en cuyo caso los conceptos de interior y frontera concuerdan con los topológicos). Las variedades con borde juegan un papel fundamental en el Teorema de Stokes generalizado.

Un cilindro finito es una variedad con borde.

El producto cartesiano de dos o más variedades es también una variedad. La dimensión de la variedad producto es la suma de las dimensiones de sus factores. Su topología es la topología producto, y un producto cartesiano de cartas es una carta para la variedad producto. Si los atlas utilizados definen una estructura diferenciable en los factores, el atlas producto define una estructura diferenciable en la variedad producto. Si uno de los factores tiene borde, la variedad producto también tendrá borde.

Los productos cartesianos pueden utilizarse para construir toros y cilindros finitos: S¹ × S¹ y S¹ × [0, 1], respectivamente.

Para realizar este procedimiento denominado suma conexa necesitamos dos variedades de la misma dimensión, de las que recortaremos una bola abierta. Este proceso dejará en cada variedad una frontera (la de la bola eliminada) que procederemos a identificar por medio de un homeomorfismo arbitrario.

En el procedimiento de suma conexa debemos crear artificialmente fronteras para después identificarlas. Si las variedades son variedades con borde, podremos identificar sus fronteras sin necesidad de crearlas previamente.

En principio, la definición de variedades prohíbe la presencia de bordes o fronteras, como un disco plano cerrado, por ejemplo. Sin embargo, es posible definir una noción de variedad con borde aceptando cartas que tengan por dominio abiertos de ${\displaystyle \mathbb {R} ^{n-1}\times \mathbb {R} _{+}^{*}}$. De este modo, el borde de una variedad así definida será una variedad de dimensión n-1. Así, una bola cerrada es una 3-variedad con borde que tiene por borde una 2-variedad, la esfera.

Un ejemplo de cociente son los espacios homogéneos. Supongamos que G es un grupo de Lie y H es un subgrupo cerrado. Entonces el cociente G/H (donde identificamos dos puntos de G si se puede pasar de uno a otro trasladándolos por algún elemento de H ), es una variedad.

En las variedades de dimensión dos y superiores, un criterio importante de invarianza es la «orientabilidad» de la variedad. Consideremos una variedad diferenciable M de dimensión m. Al igual que en superficies diferenciables, que en cada punto se puede considerar un plano tangente, a cada punto p de nuestra variedad M se le puede adjuntar un espacio vectorial de dimensión m que se suele llamar espacio tangente a M en el punto p. Este espacio vectorial se puede «orientar», es decir, escoger una base sobre la que tomar referencias, al igual que se hace en R^m con la base canónica {e_i}. Explicado vagamente, esta orientación te va a decir que cosas las estás viendo bien y qué cosas las estás viendo reflejadas (sí, como si se estuvieran viendo por medio de un espejo). Si se puede dar una «orientación» a cada espacio tangente a la variedad de forma que la orientación se parezca entre puntos parecidos, esto es siendo precisos, que para cualesquiera dos parametrizaciones φ y ψ de un entorno abierto U de un punto p de la variedad, el cambio de coordenadas phi^-1 · psi conserve la orientación canónica de R^m; entonces se dice que la variedad es orientable. Ejemplos de variedades orientables son el propio espacio euclídeo R^m, las esferas S^m, el cilindro, el toro T, o la suma conexa de g toros.

Cuando esta construcción no se puede conseguir se dice que la variedad es «no orientable». El ejemplo clásico de variedad no orientable es la cinta de Möbius. Intuitivamente, la cinta de Möebius no es orientable porque es una superficie con una sola cara, como bien ilustra M. C. Escher en su cuadro "Möbius strip II". Aquí se ve cómo andando por la superficie de la cinta de Moebius puedes pasar del «interior» al «exterior» y viceversa sin necesidad de cruzar el borde. Si uno se fija al hacer esto, la región de la cinta que tenía a la izquierda al principio, al terminar el recorrido estará a la derecha, y análogamente sucede con la región a la derecha, luego no se puede decidir qué es lo que está reflejado y qué es lo que no. La botella de Klein y el plano proyectivo real también son superficies no orientables pues contienen una cinta de Möbius; si se les pudiera dar una orientación global a una de estas superficies, entonces se le podría dar una orientación a la cinta de Möbius. Más en general, los espacios proyectivos de dimensión n par son no orientables, aunque no por este argumento con la cinta de Möebius.

La orientación de variedades topológicas, es decir, sin una estructura diferenciable, es un tema más delicado y técnico.

Una taza sólida transformándose en un toro sólido ${\displaystyle D^{2}\times S^{1}}$

Para las variedades de 2 dimensiones el género (el número de asas en una superficie) es una invariante clave: un toro es una esfera con un asa, un doble toro es una esfera con dos asas, etc. De hecho, es posible caracterizar completamente una variedad compacta de dos dimensiones por su género y su orientabilidad. En las variedades de dimensiones más altas, el género es reemplazado por la característica de Euler.

Existen numerosas aplicaciones de las variedades en matemática. El análisis real clásico y el análisis funcional han extendido su campo de investigación de los espacios vectoriales topológicos a las variedades. Del mismo modo, los procesos estocásticos como el movimiento browniano se extienden de los espacios reales de dimensión finita a las variedades. Asimismo, las variedades aparecen episódicamente en estadística. Por otro lado, muchos conjuntos interesantes tienen al mismo tiempo una estructura algebraica y una estructura de variedad «compatibles». Es el caso del conjunto de las rotaciones en un espacio de 3 dimensiones, que forma una 3-variedad y un grupo. La teoría de los grupos de Lie estudia estas variedades con propiedades algebraicas. La teoría de los espacios homogéneos estudia sus acciones transitivas.

Geómetras que estudiaron la topología de variedades:

• Riemann
• Hermann Weyl
• Shiing-Shen Chern