Mécanique des fluides numérique
La mécanique des fluides numérique (MFN), plus souvent désignée par le terme anglais computational fluid dynamics (CFD), consiste à étudier les mouvements d'un fluide, ou leurs effets, par la résolution numérique des équations régissant le fluide. En fonction des approximations choisies, qui sont en général le résultat d'un compromis en termes de besoins de représentation physique par rapport aux ressources de calcul ou de modélisation disponibles, les équations résolues peuvent être les équations d'Euler, les équations de Navier-Stokes, etc.
Pour les articles homonymes, voir CFD.
La MFN a grandi d'une curiosité mathématique pour devenir un outil essentiel dans pratiquement toutes les branches de la dynamique des fluides, de la propulsion aérospatiale aux prédictions météorologiques en passant par le dessin des coques de bateaux. Dans le domaine de la recherche, cette approche est l'objet d'un effort important, car elle permet l'accès à toutes les informations instantanées (vitesse, pression, concentration) pour chaque point du domaine de calcul, pour un coût global généralement modique par rapport aux expériences correspondantes.
Méthodologie
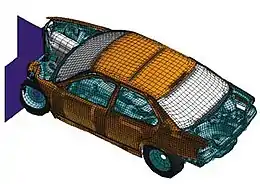
De manière générale, la résolution d'un problème de MFN passe par trois grandes phases :
- la préparation du problème : ceci passe par la définition d'une géométrie, d'un maillage discrétisant le domaine de calcul, du choix des modèles et méthodes numériques employés ;
- la résolution numérique du problème qui passe par l'exécution d'un programme informatique. Bien des problèmes suscitant un minimum d'intérêt nécessitent des ordinateurs aux très grandes capacités ;
- l'exploitation des résultats : on vérifie d'abord leur cohérence, puis ils sont examinés afin d'apporter des réponses aux questions posées par le problème de MFN de départ.
L'exploitation des résultats passe le plus souvent par des logiciels de post-traitement scientifique utilisés dans de nombreuses branches de la physique, ou bien par les modules de post-traitement disponibles dans certains logiciels de MFN commerciaux.
Méthode des différences finies
La méthode des différences finies a une importance historique et est simple à programmer. Elle n'est actuellement utilisée que dans quelques codes spécialisés.
Méthode des volumes finis
La méthode des volumes finis est une approche commune utilisée dans les codes MFN. Les équations qui régissent le fluide sont résolues sur des volumes de contrôle discret.
Méthode des éléments finis
La méthode des éléments finis (MEF) est utilisée dans l'analyse structurale des solides, mais est également applicable aux fluides. Cependant, la formulation à éléments finis nécessite des soins particuliers pour assurer une solution conservative.
Résolution du problème discrétisé
Forme générale des équations
La méthode consiste à résoudre des équations aux dérivées partielles (ÉDP) dites « équations de transport » ou « de conservation », et dont la forme générale est, pour une quantité scalaire φ donnée :
où
- φ peut désigner :
- 1 (le nombre un) dans le cas de l'équation de continuité,
- les composantes du vecteur vitesse u, v et w,
- l'enthalpie h ;
- est le volume concerné et est la surface délimitant ce volume ;
- dV est le volume d'un élément infinitésimal de et le vecteur aire d'un élément infinitésimal de ;
- est l'opérateur nabla ;
- ρ est la masse volumique ;
- est le vecteur vitesse eulérienne d'une particule fluide ;
- Dφ est un coefficient de diffusion ;
- Sφ est un terme source, ou puits.
Maillage, symétries et périodicités
Le maillage consiste à découper l'espace en cellules appelées « volumes de contrôle ». Le maillage est souvent plus délicat en mécanique des fluides que pour les éléments finis en résistance des matériaux : il faut mailler tout l'espace « vide » (la veine fluide), et les détails de surface ont de l'importance (puisqu'il génèrent des turbulences), on a donc souvent des maillages contenant de nombreuses mailles (typiquement plusieurs millions). Par ailleurs, alors qu'en résistance des matériaux, un maillage hexaédrique de l'espace est une stratégie intéressante (elle permet d'avoir la même qualité de résultats pour un nombre de nœuds plus faibles), en MFN, cela introduit des directions préférentielles qui peuvent avoir une influence sur le résultat (voir ci-après Diffusion numérique).
Dans certains domaines, les pratiques professionnelles imposent parfois un maillage hexaédrique. Sinon, la stratégie retenue est souvent :
- à proximité des parois, avoir un maillage parallèle à la paroi — hexaédrique ou bien prismatique (hexaèdres coupés en deux) — et de faible épaisseur (trois couches de cellules ayant typiquement avec un facteur y+ de l'ordre de 1, voit ci-après Modèles de turbulences) ;
- au cœur du volume, avoir un maillage tétraédrique mais n'ayant pas de direction particulière (ce ne sont pas des cubes empilés coupés en deux).
Une manière efficace de réduire la taille du modèle est d'utiliser les symétries et périodicités. Il faut pour cela que le système présente une symétrie ou une périodicité géométrique, et que les conditions limites présentent la même symétrie ou périodicité. Dans ce cas-là, les champs sortant sur une surface sont appliqués en entrée de la surface correspondante. Toutefois, il est délicat d'évaluer la pertinence de ces hypothèses. Par exemple, une condition de symétrie mal appliquée peut empêcher de voir un effet Coandă.
Il existe aujourd'hui des méthodes de maillage comme le polyhexcore[1] qui permettent de générer automatiquement des maillages de qualité et au juste besoin, avec des couches limites prismatiques à proximité des parois et des mailles parfaitement hexaédriques au cœur de la veine fluide, avec transition par mailles polyédriques entre la couche limite et le cœur. Autrefois, il fallait découper "à la main" la géométrie pour obtenir des zones hexaédriques, ce qui pouvait nécessiter beaucoup de temps. Les logiciels permettent également désormais de tirer profit du calcul parallèle pour accélérer la génération du maillage.
Il existe également des techniques de maillage totalement automatiques sans la moindre intervention humaine, comme celles mises en œuvre dans le logiciel Discovery[2]. Ces méthodes ont cependant leurs limites car le maillage ainsi généré ne contient généralement pas de couches limites et l'utilisateur ne maîtrise plus totalement l'outil, et les performances sont dynamiquement dépendantes des moyens matériels (une même géométrie sera maillée de différentes manières sur des machines différentes, conduisant à des résultats non reproductibles).
Discrétisation spatiale et temporelle des équations
La discrétisation spatiale consiste à remplacer les intégrales par des sommes sur des éléments de volume et de surface correspondant au maillage. Ainsi, pour chaque volume de contrôle (cellule), on peut écrire l'équation, en appliquant le théorème de flux-divergence :
où Δ est l'opérateur laplacien ; ou bien, avec la notation nabla :
La discrétisation temporelle consiste à faire des calculs à des instants déterminés, le résultat de la simulation à un instant ti étant la donnée d'entrée du calcul à l'instant ti + 1. Le pas de temps (ti + 1 − ti) peut être constant ou variable. La discrétion temporelle utilise typiquement la méthode des différences finies.
Cas particuliers
En prenant φ = 1, on trouve
Équation de bilan de la quantité de mouvement
En prenant φ = u (composante du vecteur vitesse sur l'axe x de vecteur directeur unitaire ), on trouve
où
- p est la pression ;
- [τ] est le tenseur des contraintes dû à la viscosité ;
- est la flottabilité (poussée d'Archimède).
En prenant φ = htot (enthalpie totale),
on trouve
où
- p est la pression ;
- λ est la conductivité thermique ;
- T est la température absolue ;
- est la conduction thermique ;
- est le travail des forces visqueuses ;
- est la source d'enthalpie, typiquement la variation d'enthalpie due à un changement d'état (chaleur latente) ou à une réaction chimique (réaction exothermique ou endothermique).
État stationnaire ou transitoire
Un état stationnaire est une situation pour laquelle le terme transitoire est nul ; on néglige donc le premier terme des équations ci-dessus
- .
Il s'agit d'un régime établi, d'un état de fonctionnement « longtemps » après le démarrage du système (ouverture du robinet, démarrage de la turbine) ; le résultat est indépendant du temps, il n'y a pas de discrétisation temporelle. Cette situation simplifie grandement les calculs.
Cependant, cela ne permet pas de prendre en compte des fluctuations des conditions d'entrée ou de sortie, ou bien la description d'un remplissage. Dans ces cas-là, il faut faire un calcul transitoire (« instationnaire »), c'est-à-dire à plusieurs instants successifs.
Si le pas de temps est trop grand, on introduit des erreurs numériques qui se propagent. Par ailleurs, cela peut rendre compliqué la convergence à chaque étape (voir ci-dessous Conditions aux limites). Mais plus le pas de temps est petit, plus le calcul est long et gourmand en ressources. Pour trouver un compromis, on s'attache en général à ce qu'une particule de fluide parcoure moins d'une maille entre chaque pas de calcul, c'est-à-dire à avoir un nombre de Courant, appelé dans le milieu CFL (condition de Courant, Friedrichs et Lewy), en général compris entre 0.1 et 0.6 (parfois plus dans le cas d'une résolution implicite, parfois moins selon l'application) :
- .
Diffusion numérique
La diffusion numérique est un artefact de calcul lié au maillage. Supposons qu'il y ait deux phases distinctes ; la frontière des phases passe au milieu de volumes de contrôle, la valeur des variables dans les-dits volumes est donc une « moyenne » des valeurs des deux phases. Il se crée donc un gradient artificiel local, puisque les valeurs sont potentiellement très différentes des valeurs des cellules voisines. Ce gradient s'atténue à cause du terme de diffusion des équations ; on se retrouve ainsi avec une frontière « floue », une transition « douce » des valeurs, alors que dans la réalité, il y a une transition abrupte.
Propriétés des matériaux
Les coefficients des équations sont des propriétés des matériaux. Il s'agit en général de valeurs dépendant des conditions de pression et de température :
- masse volumique ρ :
- pour un gaz, elle peut dériver de l'équation des gaz parfaits, ou d'un modèle de gaz plus complexe,
- pour un polymère fondu, on peut utiliser une équation d'état pvT,
- pour un solide (typiquement un solide immergé), on peut utiliser les modules d'élasticité, et en particulier le module d'élasticité isostatique (incompressibilité),
- si la variation de pression attendue est faible, on peut supposer que les fluides et solides sont incompressibles et donc que la masse volumique est une constante ;
- la conductivité thermique λ est une fonction de la température ; si la variation de température attendue est faible, on peut considérer qu'elle est constante ;
- la viscosité dynamique μ varie en fonction de la température, du taux de cisaillement et parfois de la pression ; on peut utiliser un modèle de type modèle de Cross ou loi d'Ostwald–de Waele ; si les vitesses et les variations de température attendues sont faibles, on peut considérer que c'est une constante.
Conditions aux limites
Pour résoudre les équations aux dérivées partielles, il faut indiquer les conditions aux limites à l'instant initial. Il s'agit en général de définir :
- sur les parois (le vecteur vitesse est nécessairement parallèle à la paroi) :
- s'il s'agit d'une paroi parfaitement glissante ou s'il faut prendre en compte la viscosité,
- la température de paroi et éventuellement le coefficient d'échange thermique si l'on résout l'équation de la chaleur ;
- sur les surfaces ouvertes :
- s'il s'agit d'une entrée ou d'une sortie (le flux est à sens unique), ou éventuellement s'il s'agit d'une ouverture dans laquelle le flux peut être dans les deux sens (introduit des instabilités numériques),
- imposer un champ de vitesse ou un débit, ou bien imposer une pression statique moyenne,
- imposer une température uniforme ou un flux d'enthalpie si l'on résout l'équation de la chaleur.
Lors de la définition des conditions aux limites, il faut prendre en compte la stabilité du calcul : la résolution des équations se fait de manière approchée, en plusieurs étapes, et il importe que l'on se rapproche à chaque étape de la solution (convergence, calcul stable). Voir par exemple pour illustrer ce point l'article Méthode de Newton » Exemples de non convergence.
Les conditions aux limites donnant le calcul le plus stable sont :
- une entrée sur laquelle on impose une vitesse ou un débit ;
- une sortie sur laquelle on impose une pression.
L'inverse — pression imposée en entrée, vitesse ou débit imposé en sortie — est un peu moins stable mais se résout bien. Par contre, le fait de définir une pression en entrée et en sortie, ou bien un flux (vitesse ou débit) en entrée et en sortie, débouche en général sur un calcul instable (le logiciel n'arrive pas à s'approcher de la solution).
Modèles de turbulence

Il existe essentiellement trois manières de prendre en compte les turbulences.
La première méthode consiste à avoir un maillage plus fin que le plus petit tourbillon attendu. On parle de simulation directe (DNS, direct numerical simulation). Cette méthode est extrêmement gourmande en ressources et en temps, et est donc rarement utilisée dans un contexte industriel.
Les autres méthodes consistent à simplifier les petites perturbations. Cela donne lieu à deux méthodes :
- la simulation des grandes échelles (SGE, ou LES, large eddy simulation) : le maillage est plus grossier que précédemment, les tourbillons plus fins que le maillage sont pris en compte par un modèle physique (moyenne spatiale des équations de Navier-Stokes), seuls les grand tourbillons sont simulés ;
- le moyennage temporel des équations de Navier-Stokes pour toutes les échelles (RANS, Reynolds averaged Navier-Stokes simulation).
La méthode RANS est la plus économe en ressources et est de fait très majoritairement utilisée pour les applications industrielles.
Il existe aujourd'hui des méthodes de modélisation de la turbulence qui font appel au machine learning (un modèle IA est entraîné à partir de résultats de DNS ou de résultats expérimentaux)[3]. Ces approches peuvent être plus rapides ou plus précises que les approches physico-mathématiques "classiques".
Écoulement multiphasique

Si le système contient plusieurs fluides miscibles, on peut considérer que l'on a une seule phase (un seul matériau) dont les propriétés sont déterminées par une loi de mélange. Mais si les fluides sont non miscibles, ou si la frontière est le siège d'événements particuliers (typiquement réaction chimique, cas par exemple d'un front de flamme), il faut considérer les interfaces entre les phases ; c'est le cas typique d'un système liquide/gaz, comme de l'écoulement à l'air libre ou le remplissage d'un réservoir initialement rempli d'air. C'est aussi le cas des écoulements dans le vide, et en présence de changements de phase liquide/gaz (vaporisation, liquéfaction).
On utilise en général la méthode du volume de fluide (VOF, volume of fluid) : on détermine à chaque volume de contrôle (cellule) la fraction volumique d'un des fluides.
Pour les interactions liquide-solide où le solide est présent sous forme de petites particules, celui-ci peut être assimilé à un pseudo-fluide, comme dans l'approche dite "eulérienne granulaire" [4].
Linéarisation
À un instant donné, ces équations sont linéarisées, pour former un système d'équations linéaires, mise sous une forme matricielle :
où
- [A] est une matrice de coefficients ;
- [] est le vecteur contenant les variables des équations ;
il y a une équation matricielle de ce type par volume de contrôle (cellule du maillage). Cette linéarisation utilise en général la méthode des volumes finis.
Il n'est en général pas possible de résoudre le système d'équation pour une cellule donnée, puisque l'on ne connaît pas les conditions limites pour cette cellule. Les différentes matrices sont donc assemblées en un matrice gigantesque.
Résidus
La méthode consiste en une résolution approchée, on définit le résidu [R] comme étant :
On effectue une résolution itérative, le but à chaque itération étant de diminuer les valeurs de [R]. On s'intéresse en général à une valeur particulière, soit la valeur maximale des coefficients de [R], soit la moyenne quadratique. On arrête le processus itératif lorsque l'estimateur du résidu atteint une valeur « admissible » (ou bien après un nombre donné d'itérations, lorsque le calcul a du mal à converger). Cela ne garantit toutefois pas que la solution trouvée corresponde à la réalité. On s'attache en général à suivre une ou plusieurs grandeurs, par exemple un débit ou une pression moyenne sur une surface, et l'on vérifie que la valeur des grandeurs est stable d'une itération à l'autre.
Domaines d'application
La MFN est particulièrement employée dans les domaines des transports, pour étudier notamment le comportement aérodynamique des véhicules (automobile, aéronautique, etc.) conçus.
La MFN est également utilisée dans le domaine des installations critiques telles que les salles de serveurs. Elle permet de réaliser une représentation 3D de la salle, comprenant toutes les informations relatives aux équipements informatiques, électriques et mécaniques. On obtient une carte graduée des différentes zones de chaleur présentes, ce qui permet de détecter les zones critiques et les points chauds (ou hot spots).
Quelques exemples d'utilisation et leurs avantages :
- test de la configuration architecturale (taille, forme, climatisation, densité…), de la méthodologie de climatisation (globale, en rangée, allées froides et chaudes, confinement, avec ou sans conduits de ventilation, climatisation de type XDV, XDO…) ;
- agencement des équipements de refroidissement et de climatisation et évaluation de leur impact d'encombrement ;
- réduction de la consommation énergétique des équipements prévus dans la stratégie TI ;
- déploiement des équipements : réduction de la consommation d'énergie, équilibrage de la puissance, amélioration du routage des câbles, maximisation de l'espace utilisé, réalisation de tests des modifications avant leur déploiement, validation de la capacité de refroidissement requise, évaluation du risque d'apparition de points chauds…[5]
Méthodes de simulation de fluide
Principaux logiciels
Logiciels libres
- Code Saturne, logiciel open source développé par EDF. Il sert aux calculs d'éléments importants de centrales nucléaires.
- Gerris, logiciel libre sur maillage adaptatif hiérarchique octree utilisé en écoulements multiphasiques.
- OpenFOAM, logiciel open source distribué par la société OpenCFD Ltd.
Logiciels commerciaux
- FloEFD, FloTHERM et FloTHERM XT, de la société Mentor (Siemens).
- CFX, Fluent, Icepak et Discovery (permettant du calcul sur GPU quasiment en temps réel)[2], développés et distribués par la société ANSYS.
- StarCCM+ développé et distribué par la société CD-adapco (en) (Siemens).
- PowerFLOW développé et distribué par la société Exa Corporation.
- Tecplot, logiciel de visualisation graphique et manipulation de données maillées.
- M-Star, logiciel de mécanique des fluides optimisé pour le calcul sur GPU, basé sur la méthode Lattice-Boltzmann
Références
- (en) Zore, K., « ANSYS MOSAIC POLY-HEXCORE MESH FOR HIGH-LIFT AIRCRAFT CONFIGURATION », AeSI Annual CFD Symposium, (lire en ligne)
- (en) Hendrickson, J., « ANSYS DISCOVERY LIVE »,
- (en) Zhu, L., « Machine learning methods for turbulence modeling in subsonic flows around airfoils », Physics of Fluids, (DOI https://doi.org/10.1063/1.5061693, lire en ligne
 )
) - (en) Heng, J., « On the application of an Eulerian granular model towards dilute phase pneumatic conveying », Powder Technology, (DOI https://doi.org/10.1016/j.powtec.2017.12.069)
- http://www.kelvin-emtech.com/fr/nouvelles/62_nouvelles.sn
Voir aussi
Articles connexes
- Format et outils netCDF
- Format CGNS
- Estimation stochastique en mécanique des fluides
Liens externes
- Portail de l’informatique
- Portail de la physique