Structure stellaire
Les modèles de structure stellaire décrivent la structure interne des étoiles de différentes masses et âges, ainsi que permettent de faire des prédictions sur la luminosité, la couleur et l'évolution future de ces étoiles.

1. Noyau
2. Zone de rayonnement
3. Zone de convection
4. Photosphère
5. Chromosphère
6. Couronne
7. Tache solaire
8. Granulation
9. Éruption solaire
Transport d'énergie
À partir des différentes grandeurs mesurées et de simulations issues de différents modèles, il est possible de construire une image de l’intérieur d’une étoile, bien qu’il nous soit presque inaccessible — l’astérosismologie permettant littéralement de sonder les étoiles. En l’état actuel de nos connaissances, une étoile est structurée en différentes régions concentriques, décrites ci-après à partir du centre.
Types de transport d'énergie
Les différentes couches d'une étoile transportent l'énergie produite vers son extérieur. Le transport d'énergie est accompli principalement par convection et transfert de rayonnement, mais la conduction thermique est importante pour les naines blanches.
La convection est le mode dominant de transport d'énergie lorsque le gradient de température est suffisamment grand pour qu'une portion du gaz dans l'étoile monte graduellement via un processus adiabatique. Quand c'est le cas, cette portion de gaz flotte et continue de monter si elle est plus chaude que le gaz environnant ; si, au contraire, la portion de gaz est plus froide, elle retombe à sa hauteur originale[1].
Dans les régions des étoiles avec de basses températures et une opacité assez basse pour permettre le transport par transfert de rayonnement, c'est justement le rayonnement qui est le mode dominant de transport.
Types d'étoiles

La structure d'une étoile de la séquence principale dépend uniquement de sa masse. Pour cette section, soient des étoiles de ce type.
Pour les étoiles de masse solaire (0.3–1.5 masse solaire), la fusion nucléaire de l'hydrogène vers l'hélium se fait principalement via la chaîne proton-proton. Celle-ci n'entraîne pas un gradient de température élevé, ce qui fait que le rayonnement domine dans la portion la plus centrale des étoiles comparables au Soleil. La zone plus à l'extérieur de ces étoiles est assez froide pour que l'hydrogène soit sous forme atomique, laquelle est opaque aux photons ultraviolets, ce qui fait que la convection y domine. Somme toute, les étoiles de type solaire ont des noyaux radiatifs et des enveloppes convectives.
Pour les étoiles massives (dont la masse est de plus de 1.5 masse solaire), la température du noyau dépasse les 1.8×107 K, ce qui fait que la fusion nucléaire de l'hydrogène vers l'hélium qui domine est celle du cycle CNO. Dans ce processus, l'énergie générée est proportionnelle à la température à la puissance 17, tandis que pour le processus proton-proton, l'exposant n'était que de 4[2]. À cause de cette grande sensibilité à la température dans le noyau, le gradient de température y est suffisamment élevé pour le rendre convectif. Dans la portion extérieure de l'étoile, le gradient de température est plus bas, mais la température est assez élevée pour que l'hydrogène soit presque totalement ionisé, ce qui fait que cette portion de l'étoile est transparente aux photons ultraviolets. Somme toute, les étoiles massives ont des noyaux convectifs et des enveloppes radiatives.
Les étoiles de plus petites masses n'ont pas de zone radiative, ce qui fait que le transport d'énergie dominant est la convection, sur toute leur profondeur. Les étoiles géantes sont également tout à fait convectives[3].
Équations de structure stellaire
Le modèle le plus simple de structure stellaire est un modèle quasi statique qui suppose que l'étoile est dans un état stationnaire, i.e. qui ne change pas avec le temps, et qui est symétrique de façon sphérique. Ce modèle consiste en quatre équations différentielles du premier degré : deux décrivent comment la matière et la pression varient par rapport au rayon ; les deux autres décrivent comment la température et la luminosité varient, toujours avec le rayon[4].
Hypothèse d'équilibre thermodynamique
Dans une étoile, les modèles stellaires supposent souvent qu'il y a équilibre thermodynamique local (ETL). L'ETL n'est pas strictement atteint parce que pour une coquille (une couche de l'étoile, à un rayon r donné à partir du centre) ne « voit » pas la même température au-dessous et au-dessus d'elle. Toutefois, c'est dans la plupart des cas une bonne approximation parce que le libre parcours moyen d'un photon, , est beaucoup plus petit que la distance sur laquelle la température varie de façon considérable, i. e. .
Équations détaillées
Soient la densité de matière , la température , la pression totale (matière plus rayonnement) , la luminosité et la génération d'énergie par unité de masse . Ceci, dans une coquille sphérique d'épaisseur à une distance du centre de l'étoile.
Équilibre hydrostatique

La force vers l'extérieur de l'étoile, due au gradient de pression dans celle-ci, est exactement balancée par la force vers l'intérieur, due à la gravité.
Équation de continuité de masse
L'intégrale de l'équation de continuité de masse, à partir du centre de l'étoile () jusqu'au rayon de l'étoile () donne la masse totale de l'étoile.
Équation d'énergie
La luminosité quittant une coquille sphérique à un rayon r donne l'équation d'énergie :
où est la luminosité produite sous forme de neutrinos (qui s'échappent en quasi-totalité de l'étoile sans interagir avec la matière) par unité de masse.
Hors du noyau, il n'y a pas de production d'énergie par fusion nucléaire. Donc, hors du noyau, aucune énergie n'est générée et la luminosité est constante.
Équation de transport d'énergie
Pour le transport d'énergie par conduction :
où k est la conductivité thermique.
Pour le transport d'énergie par rayonnement :
où est l'opacité de la matière, est la constante de Stefan-Boltzmann et la constante de Boltzmann est posée à 1.
Le cas du transport d'énergie par convection est plus compliqué. L'approche phénoménologique du modèle de longueur de mélange (en)[5] donne :
où est l'indice adiabatique, c'est-à-dire le ratio des capacités thermiques du gaz.
Modèle polytropique
Le rayon et la masse se déduisent de la solution de l'équation de Lane-Emden, qui décrit la structure d'un objet dont l'équation d'état comme celle d'un polytrope, et qui est soumis à l'influence de son propre champ gravitationnel. C'est Jonathan Lane qui le premier propose cette équation, en 1870, dans un travail qui est présenté comme étant le premier visant à étudier la structure interne d'une étoile.
Polytropes
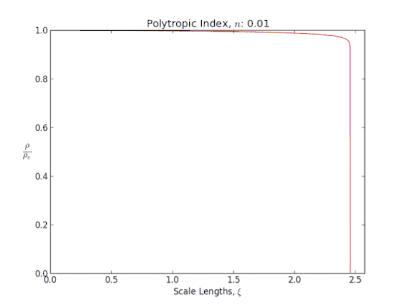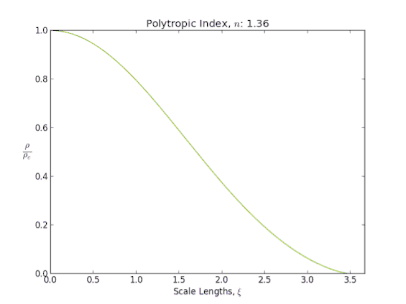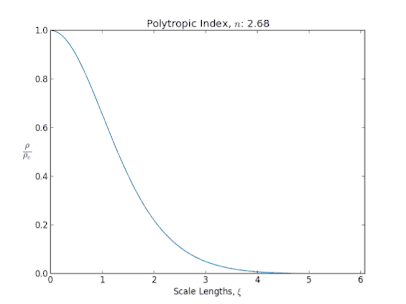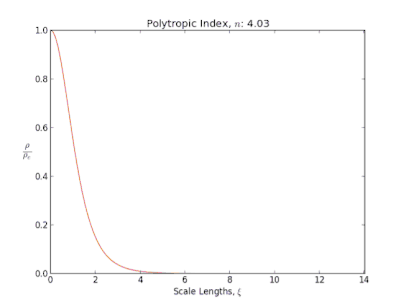
Un fluide polytropique, est un fluide dont la pression P est reliée à la masse volumique μ par l'équation d'état polytropique[6] :
- ,
où κ est une constante et γ un nombre appelé indice adiabatique. En pratique, on définit l'indice polytropique n par :
- .
La raison du choix du terme d'indice polytropique plutôt que d'indice adiabatique tient à ce qu'en pratique, il peut y avoir des échanges de chaleur au sein du fluide considéré (par exemple du fait du flux d'énergie issu des réactions de fusion nucléaire au cœur d'une étoile). Au lieu de μ, certains ouvrages utilisent ρ[7].
Solutions pour la masse et le rayon
Le rayon et la masse se déduisent de la solution de l'équation de Lane-Emden :
- .
- .
avec la quantité θ définie par
- ,
et la longueur d'échelle ξ par
- ,
r étant la coordonnée radiale en coordonnées sphériques et l'indice c désignant les quantités évaluées au centre de la configuration. Le point où s'annule est noté .
La longueur d'échelle est une variable de distance sans dimension qui provient d'avoir posé , où les constantes sont rassemblées telles que[8] :
Physique du gaz et du rayonnement
Une étoile est constituée d'un mélange d'ions, électrons et photons. Donc la physique stellaire doit couvrir les propriétés du gaz d'ions et d'électrons, les propriétés du rayonnement, ainsi que celle de leurs interactions.
Équations d'état
En thermodynamique, une équation d'état d'un système à l'équilibre thermodynamique est une relation entre différents paramètres physiques (ou variables d'état) qui déterminent son état. Dans un gaz parfait, il peut s'agir de la relation entre sa température, sa pression, sa densité et son volume. Dans une étoile, les modèles stellaires supposent souvent qu'il y a équilibre thermodynamique local (ETL) et une équation d'état relie la pression, la composition stellaire, la température et la densité[9]. À partir de l'équation d'état caractéristique d'un système physique, en particulier pour une étoile, il est possible de déterminer la totalité des quantités thermodynamiques décrivant ce système et par suite de prédire ses propriétés.
Hypothèse de l'ETL
Pour le cas des étoiles de type solaire, les interactions entre particules peuvent être négligées et l'équilibre thermodynamique local (ETL) peut être supposé. Ceci vient de que le ratio de l'énergie électrique et l'énergie cinétique est de l'ordre de 1 %[10].
Calcul
La pression totale est la somme de trois pressions : les pressions d'ions, d'électrons et de rayonnement[11].
Les ions et électrons sont considérés comme formant un gaz, donc on appelle pression du gaz la somme des deux premiers termes :
Pression d'électrons
Pour un gaz parfait et classique d'électrons :
Si les électrons sont dégénérés, alors il se produit de la pression de dégénérescence[12] :
où .
Pression de rayonnement
La pression de rayonnement est due aux photons qui transfèrent leur quantité de mouvement aux particules de gaz lorsque ceux-là sont absorbés ou dispersés[13] :
où est la constante de rayonnement. Ceci se dérive de la fonction de pression générale pour des collisions élastiques :
avec, pour la lumière, que est la quantité de mouvement, que est la vitesse des particules (i.e. de la lumière) et que est donné par la fonction de Planck.
Processus adiabatique
Selon la première loi de la thermodynamique :
et pour un processus adiabatique, il n'y a pas d'échange de d'énergie, donc dQ = 0 et finalement :
Transfert radiatif
Les modèles simples d'étoiles supposent un objet stationnaire (indépendant du temps), à symétrie sphérique et en équilibre thermodynamique local. Cette dernière hypothèse suppose que l'émission est où est donnée par la loi de Planck.
De l'hypothèse de stationnarité on peut en déduire immédiatement que le flux d'énergie sortant de la sphère définie par le rayon r est constant
Cette expression est valide à l'intérieur de l'étoile tout comme à l'extérieur.
Assombrissement du bord d'une étoile


L'observation d'une étoile montre que le bord de celle-ci est plus sombre que le centre. Ce phénomène est explicable à partir du profil d'émission dans la partie externe. Cette émission notée S et pouvant contenir un terme de diffusion varie avec la profondeur. On peut l'approcher localement par une variation linéaire en fonction de la profondeur optique comptée suivant la ligne de visée (problème de Milne)
- avec
L'intégration de l'équation de transfert fournit pour l'intensité émergente de l'étoile la valeur
L'intensité I le long d'une ligne de visée est égale à la valeur de la fonction source au point de cette ligne de visée situé à la profondeur unité. Ce résultat constitue l'approximation connue sous le nom de relation de Barbier-Eddington.
Si on se place en un point de la surface, il est facile de réaliser (figure ci-contre) que puisque l'on « voit » à τ = 1 on sonde dans la direction radiale des couches plus profondes que dans les directions proches du bord, cela à cause du facteur μ = cosθ reliant profondeur radiale et profondeur le long de la ligne de visée.
Au bord d'une étoile, comme le Soleil, on voit donc des couches plus superficielles qu'au centre. Si la température décroît vers l'extérieur, ce qui est la situation la plus générale (et en tout cas ce que prévoient tous les modèles ETL), le bord apparaîtra plus sombre que le centre. Ainsi s'explique le phénomène de l'assombrissement centre-bord sur le disque solaire.
Température effective d'une étoile
La température effective (ou apparente) est la température donnant pour un corps opaque le même flux que la valeur de l'étoile
où[14] est la constante de Stefan-Boltzmann.
Cette quantité qui vaut 5770 K pour le soleil n'est pas la température de surface de celui-ci. En effet si on calcule l'intensité émergente à l'incidence , celle-ci vaut, compte tenu de l'hypothèse ci-dessus pour le terme source
Soit un flux
Si on fait l'hypothèse de l'ETL, la fonction source en surface vaut
- où est la température vraie à la surface.
Le flux correspondant est
En comparant cette expression à celle définissant la température apparente, on voit que
Par comparaison la résolution exacte du cas gris () donne[15]
ce qui montre que l'approximation d'Eddington est assez bonne. On voit que le paramètre de température effective possède une certaine signification physique mais cela n'implique pas que le rayonnement émergent suive la loi de Planck.
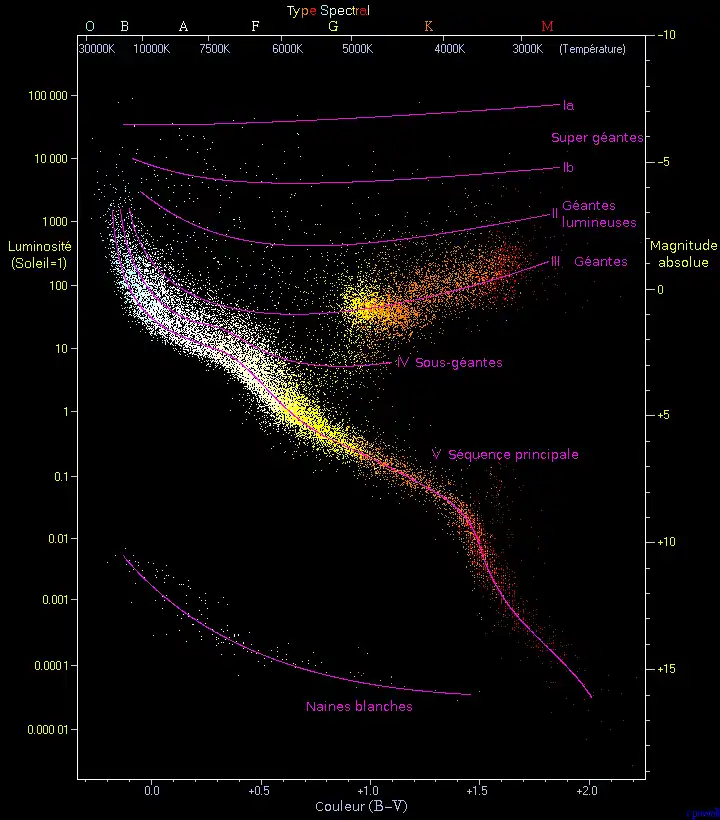
Pour reconnaître une étoile dans le ciel et en déduire ses paramètres physiques, les astronomes utilisent sa température effective et sa luminosité totale. Lorsque l'on porte les étoiles dans un diagramme basé sur ces deux paramètres (le justement célèbre diagramme de Hertzsprung-Russell, ou « diagramme HR »), les points ne se répartissent pas au hasard mais selon des séquences définies (comme la séquence principale). L'analyse de la structure de ce diagramme a permis d'établir la théorie de l'évolution d'une étoile. Les points ayant même abscisse dans ce diagramme ont même température effective et par conséquent, par définition de cette température effective, même énergie lumineuse émise par unité de surface. Il en résulte que l'ordonnée du point représentatif d'une étoile sur une même verticale est une simple mesure du carré du rayon de l'astre. Les étoiles les plus grosses (géantes ou supergéantes) sont situées dans le haut du diagramme et les plus petites (naines), dans la partie basse.
Processus nucléaires
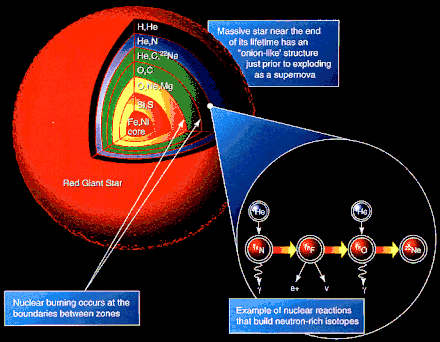
Dans les étoiles se succèdent des phases de fusion (qui peuvent avoir lieu dans le cœur même de l'étoile, ou dans les couches adjacentes à celui-ci) et de contraction. Ces fusions successives vont produire tous les éléments que l'on connait, jusqu'au fer.
Au début de la vie d'une étoile se trouve un nuage de gaz (principalement de l'hydrogène), qui, pour une raison ou une autre[note 1], va commencer à se contracter. Avec la contraction, la température augmente progressivement. Quand elle dépasse 10 millions de kelvins la température est suffisante pour que les noyaux d'hydrogène aient assez d'énergie pour vaincre la barrière coulombienne et ainsi fusionner. L'énergie libérée va contrebalancer l'effet de la gravité, et l'étoile atteint un premier équilibre.
L'hydrogène disponible à ce moment-là a été synthétisé lors du Big Bang.
Fusion de l'hydrogène
L'hydrogène est le carburant majeur des étoiles et sa fusion est le premier maillon de la chaîne de nucléosynthèse. Il y a deux manières de transformer l'hydrogène en hélium :
- le cycle proton-proton permet de transformer de l'hydrogène en 4He. Ce cycle est divisé en plusieurs réactions. La première réaction de ce cycle permet la transformation d'un proton et d'un neutron en deutérium. Ensuite, selon ce qui est disponible au cœur de l'étoile (donc selon le moment de son évolution auquel se produit cette réaction), par l'intermédiaire du tritium ou de l'hélium 3 avec lesquels les atomes de deutérium vont fusionner, l'étoile va fabriquer de l'hélium 4 ;
- le cycle CNO lui se produit à plus haute température, car les atomes qui vont fusionner lors de ce cycle ont des masses atomiques beaucoup plus élevées que l'hydrogène. Une autre condition pour que ce cycle puisse participer à la synthèse d'éléments, c'est que les éléments carbone, oxygène et azote soient présents dans le cœur de l'étoile. La figure détails du cycle CNO en précise le cycle. Comme on peut le voir ce cycle se décompose en trois sous-cycles (I, II et III), qui vont chacun produire différents isotopes qui serviront de base au sous-cycle suivant.
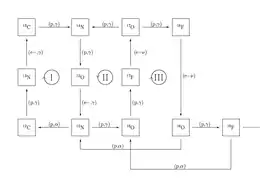
Globalement, la réaction de fusion de l'hydrogène peut s'écrire de la manière suivante[note 2] :
- .
Cette réaction de fusion de l'hydrogène est la plus exothermique de toutes les réactions qui vont se produire au cœur des étoiles. Comme les étoiles sont composées majoritairement d'hydrogène, elles disposent à ce moment de leur vie d'une grande quantité de combustible, qui leur fournit donc une grande quantité d'énergie. Cela explique pourquoi les étoiles passent la plus grande partie de leur existence dans cette phase de combustion de l'hydrogène.
Au bout d'un temps dépendant de la masse de l'étoile, la quantité d'hydrogène dans le cœur de l'étoile finit par ne plus être suffisante pour entretenir un taux de réaction assez élevé pour contrebalancer l'effet de la gravitation. Le cœur de l'étoile va alors se contracter. Lors de cette contraction, sa température va augmenter (comme n'importe quel gaz que l'on comprime) de même que sa densité. Quand la température atteint quelque 108 Kelvins, la fusion de l'hélium peut s'amorcer.
Fusion de l'hélium
C'est lorsque cette réaction démarre que la structure en couches d'une étoile se forme. En effet, la température au centre de l'étoile est telle que les couches externes au noyau sont suffisamment chaudes pour que puissent s'amorcer des réactions de fusion.
Deux réactions permettent la transformation d'hélium en éléments plus lourds :
- (1)
- (2)
La réaction (2) a posé un problème à première vue insoluble. En effet on trouve une grande quantité de carbone 12C dans l'Univers. Mais des calculs théoriques ont montré que le béryllium 8Be avait une demi-vie de l'ordre de 10-16 secondes. Cela signifie qu'il est hautement improbable que l'on puisse fabriquer du 12C en quantités importantes à partir du 8Be. Pour tenter de résoudre ce problème, Fred Hoyle avait suggéré que la réaction entre le 4He et le 8Be devait être en résonance avec un niveau d'énergie inconnu du 12C. Si ce niveau résonnant existe, alors, la section efficace de la réaction numéro 2 sera considérablement augmentée, la rendant par là même possible. Quelques années après cette prédiction, des mesures en laboratoire ont montré qu'effectivement, cet état excité existait. Ce carbone disponible va pouvoir réagir lui aussi avec les atomes d'hélium présents selon la réaction suivante:
À la fin de la phase de fusion de l'hélium, le cœur de l'étoile est donc composé majoritairement de carbone 12C et d'oxygène 16O. Comme pour la fin de la fusion de l'hydrogène, ce qui se passe ensuite ne dépend que de la masse de l'étoile. Si celle-ci est suffisante, alors le cœur de l'étoile peut se contracter de nouveau. La température et la densité peuvent elles aussi augmenter, et atteindre des valeurs qui permettent successivement les fusions du carbone et du néon.
Fusions du carbone et du néon
La fusion du carbone s'amorce quand la température au cœur de l'étoile dépasse le milliard de kelvins. Trois réactions principales se produisent, pouvant former du sodium, du néon ou du magnésium 23[note 3] :
Si la température du cœur de l'étoile reste proche du milliard de degré, les deux premières réactions sont favorisées. Si au contraire, elle s'élève au-dessus de 1,1×109 Kelvins, alors, c'est la 3e réaction qui est prédominante. Et de même, quand le carbone vient à manquer, le cœur se contracte, la température s'élève.
Lorsque celle-ci dépasse 1,2×109, les atomes de néon ont suffisamment d'énergie pour que leur fusion ait lieu. Deux réactions principales ont lieu qui peuvent produire de l'oxygène ou du magnésium 24[note 4] :
La combustion du carbone et du néon produit aussi des neutrons par les réactions suivantes :
Lors du processus s les neutrons produits de ces réactions sont absorbés par des noyaux qui ainsi augmentent leur nombre de nucléons. Dans ces noyaux les neutrons excédentaires se transforment en protons en émettant un électron et un neutrino. Le processus s peut produire les noyaux jusqu'au bismuth 209.
La phase suivante fait intervenir cette fois les atomes d'oxygène.
Fusion de l'oxygène
La dernière contraction du cœur de l'étoile a conduit celui-ci à atteindre une température de plus de 2 milliards de kelvins. À cette température, les atomes d'oxygène fusionnent, et cinq principales réactions ont lieu :
Alternativement :
Les particules alpha, les neutrons et les protons libérés lors de ces réactions ont suffisamment d'énergie pour participer à la synthèse d'autres éléments. On va donc voir apparaitre lors de cette phase un grand nombre d'éléments, tels que le chlore, l'argon, le potassium, le calcium, le titane, etc.
Une fois l'oxygène épuisé, se termine la dernière phase de fusion d'éléments au cœur de l'étoile : la fusion du silicium.
Fusion du silicium
Nous sommes là dans les tout derniers moments de la vie d'une étoile. Comme on peut le voir au tableau Temps de fusion, l'étoile n'a plus que quelques heures à vivre. Le cœur s'est à nouveau contracté, et cette fois-ci, la température atteint près de 3 milliards de kelvins. Les atomes de silicium sont brisés par les photons gamma présents, et libèrent des neutrons, des protons et des particules qui vont interagir avec les atomes de 28Si présents pour former tous les éléments jusqu'au fer.
Lorsque la quantité de fer est trop importante dans le cœur, et la quantité de silicium trop faible pour soutenir la pression de rayonnement produite par la fusion, l'étoile est à la toute fin de sa vie.
Notes et références
Notes
- Par exemple le passage d'une onde de choc au travers de ce même nuage, ou le passage d'une autre étoile à proximité, etc.
- nu () représente un ou plusieurs photons contenant une partie de l'énergie libérée par la fusion sous forme de particules ; l'autre partie est sous forme d'énergie cinétique dans les particules produites de façon explosive, cette dernière énergie étant responsable de l'augmentation de température et de pression du plasma.
- Une particule alpha () est un noyau d'hélium (4He2+). Une particule p est un proton, c'est-à-dire un simple noyau d'hydrogène (1H+). Une particule n est un neutron, responsable du rayonnement bêta (10).
- Une particule gamma () est un photon de très haute énergie (à très courte longueur d'onde).
Références
- Stellar Interiors, p. section 5.1.1.
- Stellar Interiors, p. tableau 1.1.
- Stellar Interiors, p. section 2.2.1.
- Cette discussion suit, par exemple, celles de (en) Michael A. Zeilik et Stephen A Gregory, Introductory Astronomy & Astrophysics, Fort Worth, Saunders College Publishing, coll. « Saunders golden sunburst series », , 4e éd., 672 p. (ISBN 978-0-03-006228-5, OCLC 38157539) et Stellar Interiors.
- Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics, Addison-Wesley (2007)
- Horedt, G.P. ( 2004 ). Polytropes. Applications in Astrophysics and Related Fields, Dordrecht : Kluwer. (ISBN 1-4020-2350-2)
- « section 2.4 », dans Principles of Stellar Evolution and Nucleosynthesis.
- « p. 158 », dans Principles of Stellar Evolution and Nucleosynthesis.
- « p. 35 », dans Introduction to the Theory of Stellar Structure and Evolution.
- « section 3.1, p.35 », dans Introduction to the Theory of Stellar Structure and Evolution.
- « chapitre 3 », dans Introduction to the Theory of Stellar Structure and Evolution.
- « chapitre 3, équation (3.33) », dans Introduction to the Theory of Stellar Structure and Evolution.
- « section 3.4 », dans Introduction to the Theory of Stellar Structure and Evolution.
- (en) Committee on Data for Science and Technology (CODATA), in The NIST Reference on Constants, Units and Uncertainty, 2010 [présentation en ligne]
- (en) Subrahmanyan Chandrasekhar, Radiative transfer, New York, Dover Publications, , 393 p. (ISBN 978-0-486-60590-6, OCLC 335528, présentation en ligne, lire en ligne)
Sources
- (en) Carl J Hansen, Steven D Kawaler et Virginia Trimble, Stellar Interiors : physical principles, structure, and evolution, New York, Springer, coll. « Astronomy and astrophysics library », , 2e éd., 526 p. (ISBN 978-0-387-20089-7, OCLC 53083938, lire en ligne).
- (en) Donald D. Clayton, Principles of stellar evolution and nucleosynthesis, New York, McGraw-Hill, , 612 p. (ISBN 978-0-07-011295-7, OCLC 299102), section 2.4.
- Dina Prialnik, Introduction to the Theory of Stellar Structure and Evolution, Cambridge University Press, 2000, p. 35.
Autres sources
- R. Kippenhahn et A. Weigert, Stellar Structure and Evolution, Springer-Verlag,
- Dallas C. Kennedy et Sidney A. Bludman, « Variational Principles for Stellar Structure », Astrophysical Journal, vol. 484, no 1, , p. 329 (DOI 10.1086/304333, Bibcode 1997ApJ...484..329K, arXiv astro-ph/9610099)
- Achim Weiss, Wolfgang Hillebrandt, Hans-Christoph Thomas et H. Ritter, Cox and Giuli's Principles of Stellar Structure, Cambridge Scientific Publishers,
- Subrahmanyan Chandrasekhar, An introduction to the study of stellar structure, Chicago, Ill., University of Chicago Press, (lire en ligne)
- Portail de l’astronomie