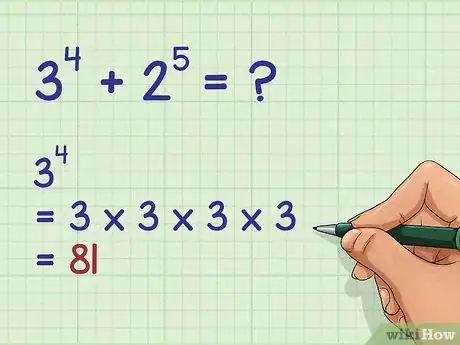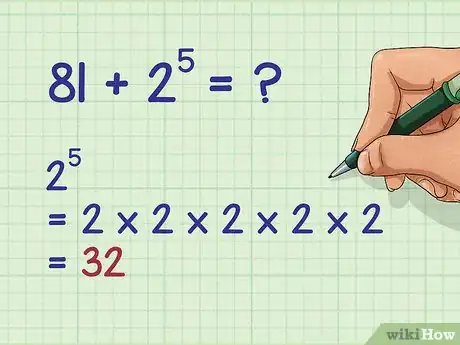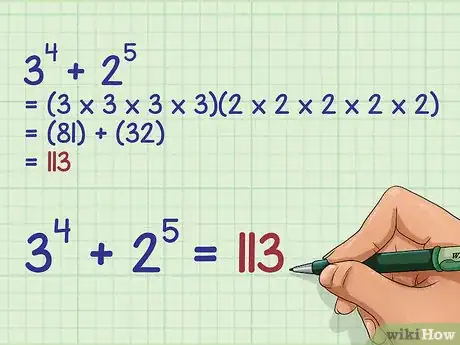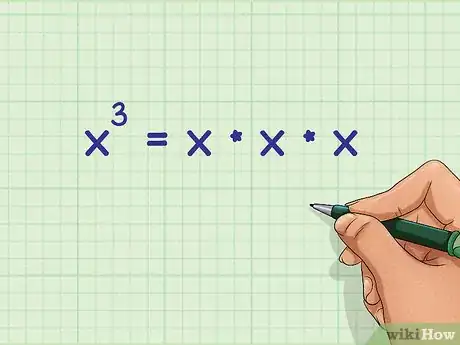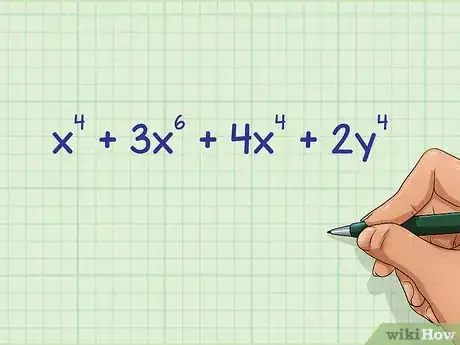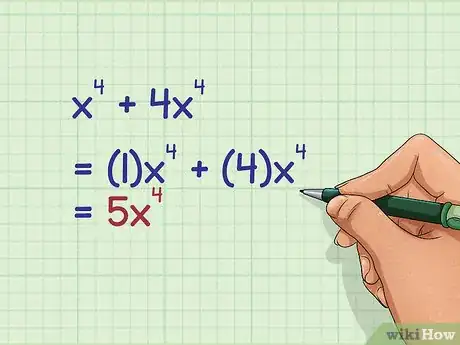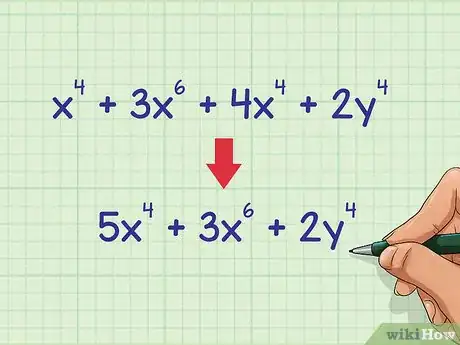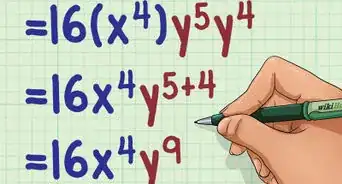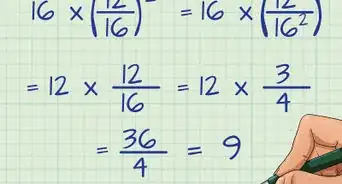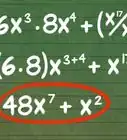How to Add Exponents

Co-authored by David Jia

Last Updated: March 25, 2023

An exponent, also called a power or index,^{[1]
X
Research source} is a number that tells you how much to multiply a base number. To solve an addition sentence that includes exponents, you must know how to find the value of the individual exponential expressions, either by hand or by using a calculator. When adding variables with exponents, you must be aware of certain rules for combining like terms.

Method 1

Method 1 of 3:

Adding Numbers With Exponents By Hand

1
Solve the first exponential expression. An exponential expression has a base (large number) and exponent (small number). The exponent tells you how many times to multiply the base by itself ( $2^{3}=2\times 2\times 2$ $2^{{3}}=2\times 2\times 2$ ).^{[2]
X
Research source}
- For example, if your problem is $3^{4}+2^{5}$ , you would first calculate $3^{4}$ :
  $3^{4}$
  $=3\times 3\times 3\times 3$
  $=81$
2
Solve the second exponential expression. To do this, multiply the base by itself the number of times indicated by the exponent.
- For example, the problem is now $81+2^{5}$ , so you need to calculate $2^{5}$ :
  $2^{5}$
  $=2\times 2\times 2\times 2\times 2$
  $=32$
Advertisement
3
Add the two values together. This will give you the sum of the two exponential expressions.
- For example:
  $3^{4}+2^{5}$
  $=(3\times 3\times 3\times 3)+(2\times 2\times 2\times 2\times 2)$
  $=(81)+(32)$
  $=113$

Method 2

Method 2 of 3:

Adding Numbers With Exponents Using a Calculator

1
Locate the exponent key on your calculator. This key will likely look like $y^{x}$ or $EXP$ , or it may look like an $x$ with a blank box as the exponent. If you do not have a scientific calculator, you cannot use this method.
2
Type in the first exponential expression. To do this, hit the base number (large number) first, then hit the exponent.
- For example, if your problem is $3^{4}+2^{5}$ , you would hit the following sequence of keys to solve the first expression:
  $3$
  $y^{x}$
  $4$
3
Hit the addition key. This will show you the value of the first exponential expression. You do not need to hit the equal key ( $=$ $=$ ) after typing in the first exponential expression.
- For example, after typing in the expression $3^{4}$ , you should hit the $+$ symbol to see a value of $81$ .
4
Type in the second exponential expression. To do this, hit the base number (large number) first, then hit the exponent.
- For example, if your problem is $3^{4}+2^{5}$ , you would hit the following sequence of keys to solve the second expression:
  $2$
  $y^{x}$
  $5$
5
Hit the equal key ( $=$ ). This will show you the final sum of the two exponential expressions.
- For example, after hitting the appropriate sequence of keys, $3^{4}+2^{5}$ adds up to $113$ .

Method 3

Method 3 of 3:

Adding Variables With Exponents

1
Find terms with the same base and the same exponent. The base is the large number (or variable) in the exponential expression, and the exponent is the small number.
- The exponent tells you how many times to multiply the base by itself ( $x^{3}=x\times x\times x$ ).^{[3]
  X
  Research source}
- In the case of variables, an exponential expression will also have a coefficient, which is a number appearing before the variable that tells you how to multiply the variable.^{[4]
  X
  Research source}
- Even if a variable has no coefficient, it is understood to have the coefficient of $1$ . For example, $x^{4}=1x^{4}$
2
Add the terms with the same base and exponent.^{[5]
X
Research source} When working with variables, there is no way to add terms that do not have the same base and the same exponent. The terms must have BOTH of these parts in common.
- For example, if the problem is $x^{4}+3x^{6}+4x^{4}+2y^{4}$ , you should note that $x^{4}$ and $4x^{4}$ have the same base ( $x$ ) and the same exponent ( $4$ ). Thus, these two terms can be added together. The term $3x^{6}$ has a different exponent, so it cannot be added; the term $2y^{4}$ has a different base, so it cannot be added.
3
Add the coefficients of the like terms. Remember, if a term has no coefficient shown, a coefficient of $1$ $1$ is understood. Do NOT add the exponents. The exponent stays the same.
- For example, if you are calculating $x^{4}+4x^{4}$ you would add together the coefficients, and $x^{4}$ would stay the same:
  $x^{4}+4x^{4}$
  $=(1)x^{4}+(4)x^{4}$
  $=5x^{4}$
4
Write out the final, simplified addition sentence. Remember, you cannot add exponential expressions that do not have the same base AND exponent, so those will stay the same as they were in the original problem.
- For example, $x^{4}+3x^{6}+4x^{4}+2y^{4}$ simplifies to $5x^{4}+3x^{6}+2y^{4}$ .

Calculator, Practice Problems, and Answers

Sample Adding Exponents Calculator

Sample Adding Exponents Practice Problems

Sample Adding Exponents Practice Answers

Community Q&A

Question

What is x cubed plus x cubed?

Community Answer

Since the two expressions have the same base (x) and the same variable (3), you can just add the coefficients. If a variable has no coefficient, it really has a coefficient of 1. The exponents will stay the same. So: x^3 + x^3 (1)x^3 + (1)x^3 2x^3
Question

How do I add x to the power of 2 plus 4x?

Community Answer

The exponents are not same, therefore it is impossible to add it.
Question

How do figure out what X squared plus X to the negative 2 is?

Community Answer

X^2 +X^-2. It cancels itself because ^2 and ^-2 are opposites. That makes X raised to the 1st. X^1 is X.