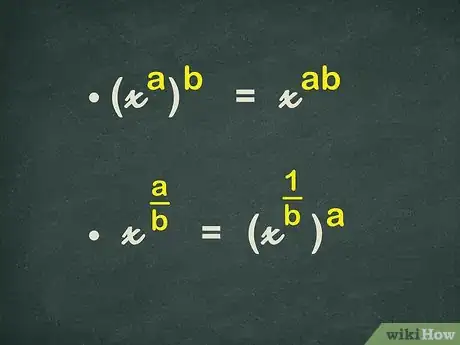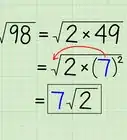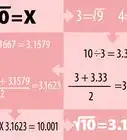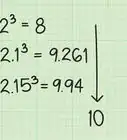This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
This article has been viewed 289,275 times.
Calculating exponents is a basic skill students learn in pre-algebra. Usually you see exponents as whole numbers, and sometimes you see them as fractions. Rarely do you see them as decimals. When you do see an exponent that is a decimal, you need to convert the decimal to a fraction. Then, there are a number of rules and laws regarding exponents you can use to calculate the expression.
Steps
Calculating a Decimal Exponent
-
1Convert the decimal to a fraction. To convert a decimal to a fraction, consider place value. The denominator of the fraction will be the place value. The digits of the decimal will equal the numerator.[1]
- For example, for the exponential expression , you need to convert to a fraction. Since the decimal goes to the hundredths place, the corresponding fraction is .
-
2Simplify the fraction, if possible. Since you will be taking a root corresponding to the denominator of the exponent’s fraction, you want the denominator to be as small as possible. Do this by simplifying the fraction. If your fraction is a mixed number (that is, if your exponent was a decimal greater than 1), rewrite it as an improper fraction.
- For example, the fraction reduces to , So,
Advertisement -
3Rewrite the exponent as a multiplication expression. To do this, turn the numerator into a whole number, and multiply it by the unit fraction. The unit fraction is the fraction with the same denominator, but with 1 as the numerator.
- For example, since , you can rewrite the exponential expression as .
-
4Rewrite the exponent as a power of a power. Remember that multiplying two exponents is like taking the power of a power. So becomes .[2]
- For example, .
-
5Rewrite the base as a radical expression. Taking a number by a rational exponent is equal to taking the appropriate root of the number. So, rewrite the base and its first exponent as a radical expression.
- For example, since , you can rewrite the expression as .[3]
-
6Calculate the radical expression. Remember that the index (the small number outside the radical sign) tells you which root you are looking for. If the numbers are cumbersome, the best way to do this is using the feature on a scientific calculator.
- For example, to calculate , you need to determine which number multiplied 4 times is equal to 81. Since , you know that . So, the exponential expression now becomes .
-
7Calculate the remaining exponent. You should now have a whole number as an exponent, so calculating should be straightforward. You can always use a calculator if the numbers are too large.
- For example, . So, .
Solving a Sample Problem
-
1Calculate the following exponential expression: .
-
2Convert the decimal to a fraction. Since is greater than 1, the fraction will be a mixed number.
- The decimal is equal to , so .
-
3Simplify the fraction, if possible. You should also convert any mixed numbers to improper fractions.
- Since reduces to , .
- Converting to an improper fraction, you have . So, .
-
4Rewrite the exponent as a multiplication expression. Since , you can rewrite the expression as .
-
5Rewrite the exponent as a power of a power. So, .
-
6Rewrite the base as a radical expression. , so you can rewrite the expression as .
-
7Calculate the radical expression. . So, the expression is now .
-
8Calculate the remaining exponent. . So,
Understanding Exponents
-
1Recognize an exponential expression. An exponential expression has a base and an exponent. The base is the large number in the expression. The exponent is the smaller number.[4]
- For example, in the expression , is the base and is the exponent.
-
2Identify the parts of an exponential expression. The base is the number that is being multiplied. The exponent tells you how many times the base is being used as a factor in the expression.[5]
- For example, .
-
3Identify a rational exponent. A rational exponent is also called a fractional exponent. It is an exponent that takes the form of a fraction.[6]
- For example, .
-
4Understand the relationship between radicals and rational exponents. Taking a number to the power is like taking the square root of the number. So, . The same is true for other roots and exponents. The denominator of the exponent will tell you which root to take:[7]
- For example, . You know that 3 is the fourth root of 81 since
-
5Understand the exponential law of powers of powers. This law says that . In other words taking an exponent to another power is the same as multiplying the two exponents.[8]
Expert Q&A
Did you know you can get expert answers for this article?
Unlock expert answers by supporting wikiHow
-
QuestionHow can you easily calculate a decimal exponent?
 David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
-
QuestionWhy do you calculate the root before the exponent?
 David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
David JiaDavid Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
-
QuestionHow do I find 15^1.4?
 DonaganTop AnswererFirst convert 1.4 to 14/10, and reduce to 7/5. An exponent of 7/5 means first raising to the seventh power and then finding the fifth root (or first finding the fifth root and then raising to the seventh power). Thus, in this case you would raise 15 to the seventh power and then find that number's fifth root.
DonaganTop AnswererFirst convert 1.4 to 14/10, and reduce to 7/5. An exponent of 7/5 means first raising to the seventh power and then finding the fifth root (or first finding the fifth root and then raising to the seventh power). Thus, in this case you would raise 15 to the seventh power and then find that number's fifth root.
References
- ↑ David Jia. Academic Tutor. Expert Interview. 14 January 2021.
- ↑ http://www.mathsisfun.com/algebra/exponent-fractional.html
- ↑ https://www.youtube.com/watch?v=Nh_qarbfsWA
- ↑ https://www.mathsisfun.com/exponent.html
- ↑ https://www.mathsisfun.com/exponent.html
- ↑ http://www.mathsisfun.com/algebra/exponent-fractional.html
- ↑ http://www.purplemath.com/modules/exponent5.htm
- ↑ https://www.cuemath.com/algebra/exponent-rules/
- ↑ https://www.cuemath.com/algebra/exponent-rules/
- ↑ David Jia. Academic Tutor. Expert Interview. 14 January 2021.
About This Article
To solve a decimal exponent, start by converting the decimal to a fraction, then simplify the fraction. Next, rewrite the fraction as a multiplication expression. To finish, rewrite the exponent as the power of a power, then turn the base and its first exponent into a radical expression by finding the root of the number. Calculate the radical expression, using the x root y function on a calculator if necessary, and the remaining exponent from the exponent. For tips on understanding exponents, including how to identify a rational exponent, read on!





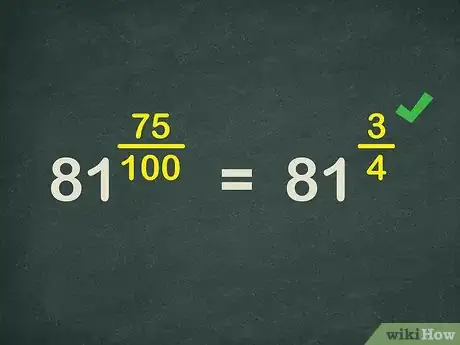


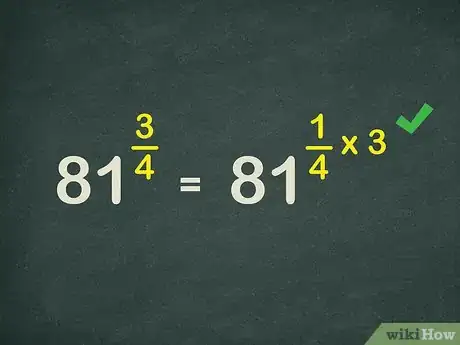


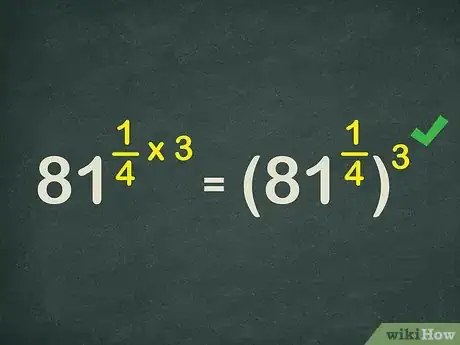



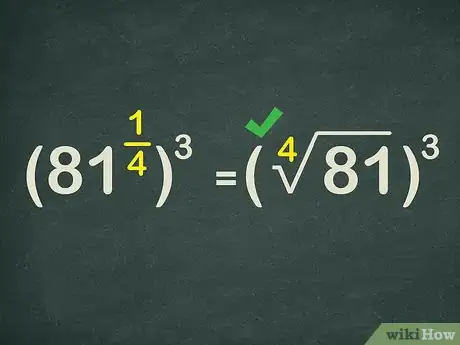
![81^{{{\frac {1}{4}}}}={\sqrt[ {4}]{81}}](./images/1729896335-b37415d73d383d0450962dda1cf0ddb2e0da0452.webp)
![({\sqrt[ {4}]{81}})^{{3}}](./images/1878007873-79a4e12743be369be81296fe2aeabd97c70cb9ab.webp)
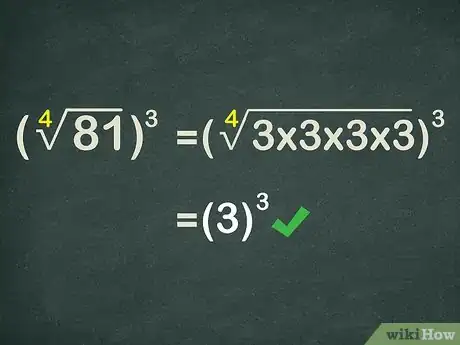
![{\sqrt[ {x}]{y}}](./images/1733107567-58c28156258e3c4cf15e8af14abcc0163150e3e6.webp)
![{\sqrt[ {4}]{81}}](./images/1841110937-44f5722ccf46fec0200534e84bda483bc2b726b1.webp)

![{\sqrt[ {4}]{81}}=3](./images/1590632178-44d91764f62522cec7024ef6481f0b83305f17e9.webp)

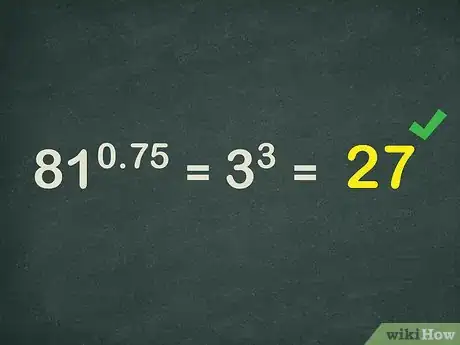


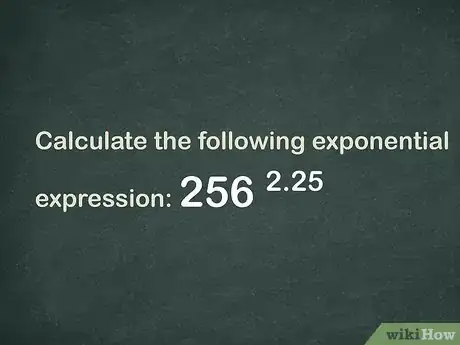






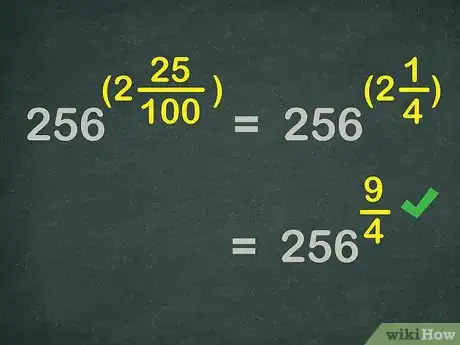




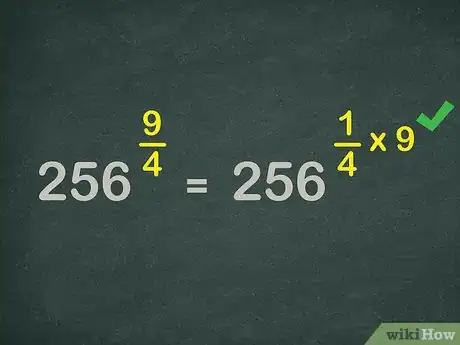


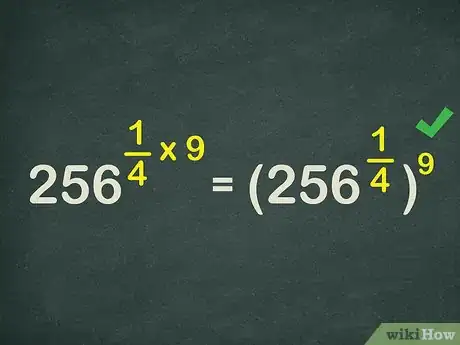

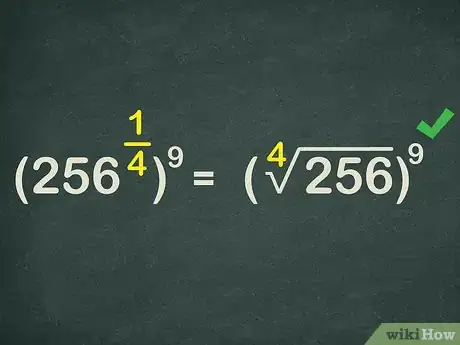
![256^{{{\frac {1}{4}}}}={\sqrt[ {4}]{256}}](./images/2244026551-cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4.webp)
![({\sqrt[ {4}]{256}})^{{9}}](./images/1315184169-261990049bf6155622a73330e280af3d17084588.webp)
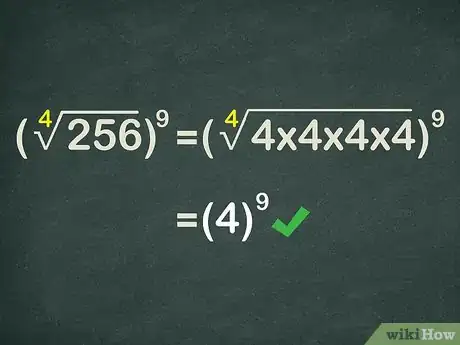
![{\sqrt[ {4}]{256}}=4](./images/2117541890-55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476.webp)

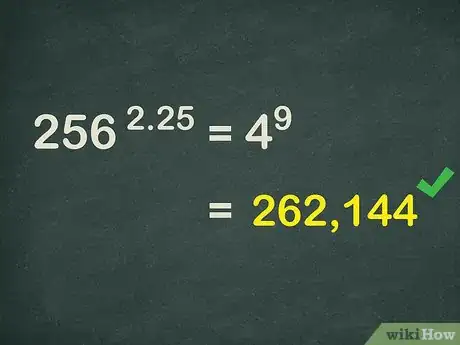






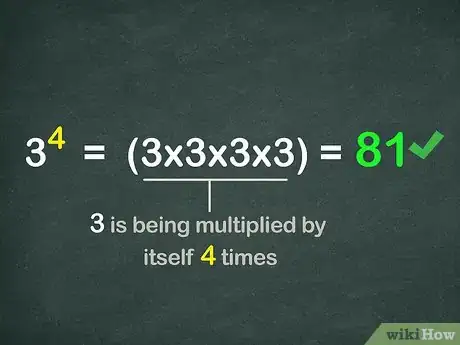



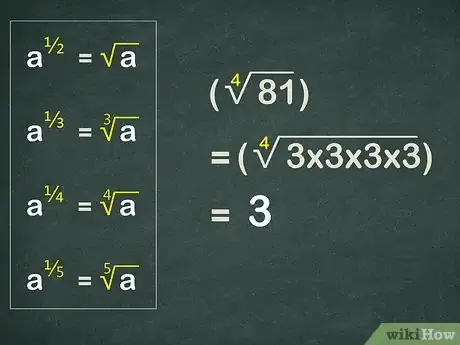


![x^{{{\frac {1}{3}}}}={\sqrt[ {3}]{x}}](./images/2160271401-759eade6ce89e27b301ccdcd83d7e8858827b8e2.webp)
![x^{{{\frac {1}{4}}}}={\sqrt[ {4}]{x}}](./images/1811226489-625ea5fe7631555b2fc23ac21f595d7c20633ec9.webp)
![x^{{{\frac {1}{5}}}}={\sqrt[ {5}]{x}}](./images/1955799054-788c8c448ea3cf9b81867b10ba6bbb1a47abb388.webp)
![81^{{{\frac {1}{4}}}}={\sqrt[ {4}]{81}}=3](./images/2053775506-0af496f05893da79ec2c45b4ebebabce0930dce0.webp)