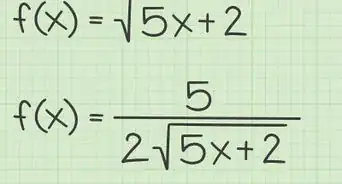How to Find the Limit of a Function

Last Updated: October 5, 2020

Finding the limits of functions is a fundamental concept in calculus. Limits are used to study the behaviour of a function around a particular point. Computing limits involves many methods, and this article outlines some of those.

Steps

1
Use the method of direct substitution. If, for example, we have ${\displaystyle \lim _{x\to 4}(x+4)}$ , plug in $4$ where $x$ is. That gives us $8$ . The limit of $f$ , where $f(x)=x+4$ , at $x=4$ is $8$ . This might not always work, though; when the problem involves rational functions with a variable in the denominator, like $\lim _{x\to 2}{\frac {\mathrm {x^{2}-4} }{\mathrm {x-2} }}$ , substituting $2$ for $x$ will cause the function to equal ${\frac {\mathrm {0} }{\mathrm {0} }}$ , giving you an indeterminate form. Or, if you get an undefined result where the numerator is a non-zero value and the denominator is $0$ , the limit does not exist.
2
Try factoring out and cancelling terms that lead to ${\frac {\mathrm {0} }{\mathrm {0} }}$ or ${\frac {\mathrm {\infty } }{\mathrm {\infty } }}$ . In the previous example $\lim _{x\to 2}{\frac {\mathrm {x^{2}-4} }{\mathrm {x-2} }}$ , we can factor out and cancel $x-2$ : $\lim _{x\to 2}{\frac {\mathrm {(x-2)(x+2)} }{\mathrm {x-2} }}$ = ${\displaystyle \lim _{x\to 2}(x+2)}$ . We can evaluate it by plugging in $2$ and the limit is $4$ .

Advertisement
3
Try to multiply the numerator and the denominator with a conjugate. We have $\lim _{x\to 4}{\frac {\mathrm {2-{\sqrt {x}}} }{\mathrm {4-x} }}$ . If you multiply the numerator and denominator with $(2+{\sqrt {x}})$ will transform it into $\lim _{x\to 4}{\frac {\mathrm {4-x} }{\mathrm {(4-x)(2+{\sqrt {x}})} }}$ . You can cancel out $(4-x)$ to get a simpler $\lim _{x\to 4}{\frac {\mathrm {1} }{\mathrm {2+{\sqrt {x}}} }}$ . This comes up to ${\frac {\mathrm {1} }{\mathrm {4} }}$ .
4
Use trigonometric transformations. If your limit is $\lim _{\theta \to 0}{\frac {\mathrm {1-cos\theta } }{\mathrm {\theta } }}$ , multiply the numerator and denominator with $(1+cos\theta )$ to get $\lim _{\theta \to 0}{\frac {\mathrm {1-cos^{2}\theta } }{\mathrm {(\theta )(1+cos\theta )} }}$ . Use $sin^{2}\theta +cos^{2}\theta =1$ and separate the multiplied fractions to obtain $\lim _{\theta \to 0}sin\theta$ $*$ ${\frac {\mathrm {sin\theta } }{\mathrm {\theta } }}$ $*$ ${\frac {\mathrm {1} }{\mathrm {(1+cos\theta )} }}$ . You can plug in $0$ to get $0*1*1$ . The limit is $0$ .
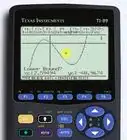
5
Find limits at infinity. $\lim _{x\to 0}{\frac {\mathrm {1} }{\mathrm {x} }}$ has a limit at infinity. It cannot be simplified to be a finite number. Examine the graph of the function if this is the case. For the limit in the example, if you look at the graph of $y={\frac {\mathrm {1} }{\mathrm {x} }}$ , you will see that ${\displaystyle y\to \infty }$ as ${\displaystyle x\to 0}$ .
6
Use L'Hôpital's rule. This is used for indeterminate forms like ${\frac {\mathrm {0} }{\mathrm {0} }}$ or ${\frac {\mathrm {\infty } }{\mathrm {\infty } }}$ . This rule states that for functions f and h differentiable on an open interval I except at a point c in I, if ${\displaystyle \lim _{x\to c}f(x)}$ = ${\displaystyle \lim _{x\to c}h(x)}=0$ or ${\displaystyle \lim _{x\to c}f(x)}$ = ${\displaystyle \lim _{x\to c}h(x)}=\pm \infty$ and ${\displaystyle h'(x)\neq 0}$ for all ${\displaystyle x\neq c}$ in $I$ and if $\lim _{x\to c}{\frac {\mathrm {f'(x)} }{\mathrm {h'(x)} }}$ exists, $\lim _{x\to c}{\frac {\mathrm {f(x)} }{\mathrm {h(x)} }}=\lim _{x\to c}{\frac {\mathrm {f'(x)} }{\mathrm {h'(x)} }}$ . This rule converts indeterminate forms to forms that can be easily evaluated. For example, $\lim _{\theta \to 0}{\frac {\mathrm {sin\theta } }{\mathrm {\theta } }}$ = $\lim _{\theta \to 0}{\frac {\mathrm {cos\theta } }{\mathrm {1} }}$ = ${\frac {\mathrm {1} }{\mathrm {1} }}$ = $1$ .

Community Q&A

Question

How can I find the limit of a function using trigonometric identities?

Linnie

Top Answerer

If your limit involves trigonometric terms, such as sine or cosine, try to replace parts of the function with alternative forms of the terms if direct substitution gives you an indeterminate form. For example, if your function is f(x) = (1 - cos²x)/(sinx), you could replace 1 - cos²x with sin²x (as sin²x + cos²x = 1) and then cancel the sinx in the denominator, leaving you with f(x) = sinx.
Question

What should I do if direct substitution gives me 0/0?

Linnie

Top Answerer

If directly substituting results in the function equalling 0/0, try factoring, multiplying by conjugates, using alternative forms of trigonometric functions, or L'Hopital's rule to discover the limit. If none of these methods can be used, approximate the limit from a graph or table or by substituting nearby values at different intervals.