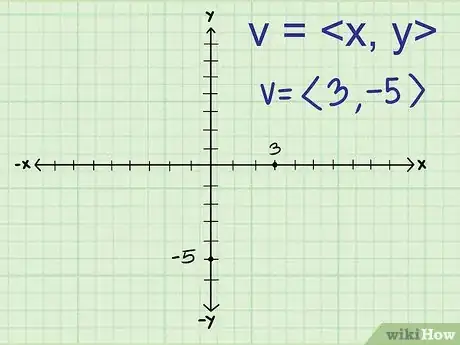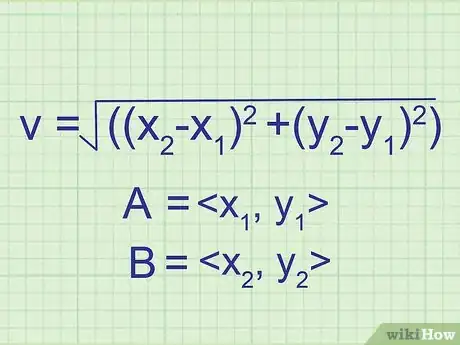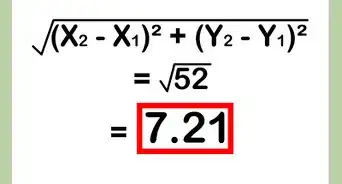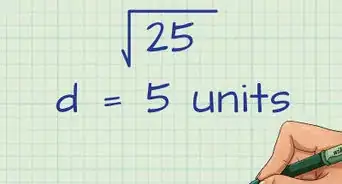wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 17 people, some anonymous, worked to edit and improve it over time.
wikiHow marks an article as reader-approved once it receives enough positive feedback. In this case, 82% of readers who voted found the article helpful, earning it our reader-approved status.
This article has been viewed 793,547 times.
Learn more...
A vector is a geometrical object that has both a magnitude and direction.[1] The magnitude is the length of the vector, while the direction is the way it's pointing. Calculating the magnitude of a vector is simple with a few easy steps. Other important vector operations include adding and subtracting vectors, finding the angle between two vectors, and finding the cross product.
Steps
Finding the Magnitude of a Vector at the Origin
-
1Determine the components of the vector. Every vector can be numerically represented in the Cartesian coordinate system with a horizontal (x-axis) and vertical (y-axis) component.[2] It is written as an ordered pair .
- For example, the vector above has a horizontal component of 3 and a vertical component of -5, therefore the ordered pair is <3, -5>.
-
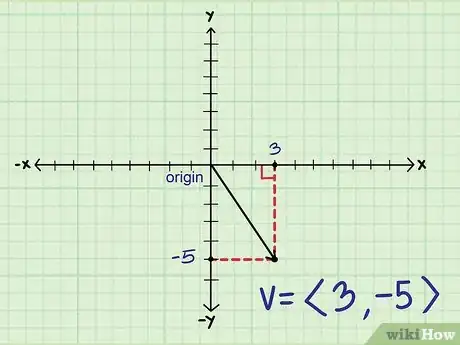
2Draw a vector triangle. When you draw the horizontal and vertical components, you end up with a right triangle. The magnitude of the vector is equal to the hypotenuse of the triangle so you can use the Pythagorean theorem to calculate it.[3]Advertisement
-
3Rearrange the Pythagorean theorem to calculate the magnitude. The Pythagorean theorem is A2 + B2 = C2. “A” and “B” are the horizontal and vertical components of the triangle while “C” is the hypotenuse. Since the vector is the hypotenuse you want to solve for “C”.[4]
- x2 + y2 = v2
- v = √(x2 + y2))
-
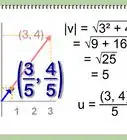
4Solve for the magnitude. Using the equation above, you can plug in the numbers of the ordered pair of the vector to solve for the magnitude.[5]
- For example, v = √((32+(-5)2))
- v =√(9 + 25) = √34 = 5.831
- Don't worry if your answer is not a whole number. Vector magnitudes can be decimals.
Finding the Magnitude of a Vector Away from the Origin
-
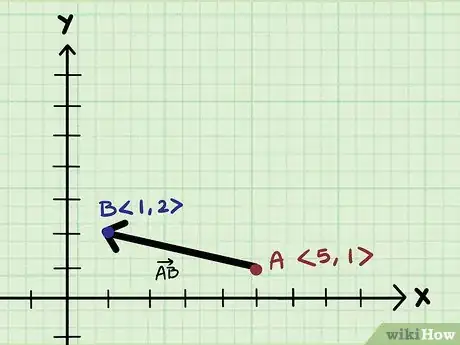
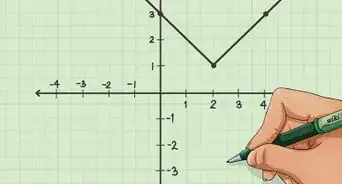
1Determine the components of both points of the vector. Every vector can be numerically represented in the Cartesian coordinate system with a horizontal (x-axis) and vertical (y-axis) component.[6] It is written as an ordered pair . If you are given a vector that is placed away from the origin of the Cartesian coordinate system, you must define the components of both points of the vector.
- For example, the vector AB has an ordered pair for point A and point B.
- Point A has a horizontal component of 5 and a vertical component of 1, so the ordered pair is <5, 1>.
- Point B has a horizontal component of 1 and a vertical component of 2, so the ordered pair is <1, 2>.
-
2Use a modified formula to solve for the magnitude. Because you now have two points you are dealing with, you must subtract the x and y components of each point before you solve using the equation v = √((x2-x1)2 +(y2-y1)2).[7]
- Point A is ordered pair 1 <x1, y1> and point B is ordered pair 2 <x2, y2>
-
3Solve for the magnitude. Plug in the numbers of your ordered pairs and calculate the magnitude. Using our above example the calculation looks like this:[8]
- v = √((x2-x1)2 +(y2-y1)2)
- v = √((1-5)2 +(2-1)2)
- v = √((-4)2 +(1)2)
- v = √(16+1) = √(17) = 4.12
- Don't worry if your answer is not a whole number. Vector magnitudes can be decimals.
Community Q&A
-
QuestionThe coordinates of head and tail of a vector are (2, 1, 0), (-4, 2, -3). What is the magnitude of the vector?
Community AnswerYou can use the same formula: |→a| = √((x2 – x1)^2 + (y2 – y1)^2), but add on (z2 – z1)^2 at the end for the third set of coordinates! -
QuestionHow do I find the direction?
Community AnswerUse this formula: tan(y component / x component). If the vector is in quadrant 3 or 4, add a half rotation. -
QuestionWhat is the magnitude of the resultant vector of vector A-12.66 and vector B-11.93?
Community AnswerTo get the magnitude you need to square both the vectors' magnitude and then take the underroot.
References
- ↑ https://www.mathsisfun.com/algebra/vectors.html
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Components
- ↑ https://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Addition
- ↑ https://www.cuemath.com/magnitude-of-a-vector-formula/
- ↑ https://sciencing.com/calculate-magnitude-force-physics-6209165.html
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Components
- ↑ https://www.cuemath.com/magnitude-of-a-vector-formula/
- ↑ https://math.libretexts.org/Courses/Truckee_Meadows_Community_College/TMCC%3A_Precalculus_I_and_II/Under_Construction_test2_08%3A_Further_Applications_of_Trigonometry/Under_Construction%2F%2Ftest2%2F%2F08%3A_Further_Applications_of_Trigonometry%2F%2F8.8%3A_Vectors
About This Article
To find the magnitude of a vector, first determine its horizontal and vertical components on their respective number lines around the origin. Next, draw the horizontal and vertical components to plot the point where they intersect. Then draw a line from the origin to that point, creating a vector triangle, which is a right triangle. Finally, use the Pythagorean theorem to calculate the triangle’s hypotenuse, which is the same as the vector’s magnitude. For more information on finding the magnitude of a vector, including using a modified formula when the vector is away from the origin, scroll down!
