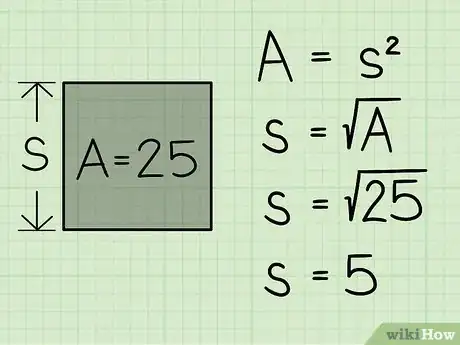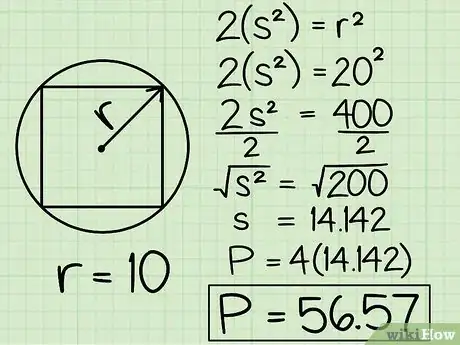Cómo calcular el perímetro de un cuadrado

El perímetro de una forma geométrica bidimensional es la distancia total alrededor de dicha forma o la suma de la longitud de sus lados.^{[1]
X
Fuente de investigación} Por definición, un cuadrado es una forma de cuatro lados rectos de igual longitud y cuatro ángulos (90 grados).^{[2]
X
Fuente de investigación} Como los cuatro lados tienen la misma longitud, ¡hallar el perímetro del cuadrado será realmente sencillo! Este artículo te mostrará la manera de calcular el perímetro de un cuadrado si conoces la longitud de un lado. Luego te mostrará la manera de hallar el perímetro de un cuadrado si solo conoces su área y, por último, te enseñará a hallar el perímetro de un cuadrado que está inscrito en un círculo con un radio conocido.

Método 1

Método 1 de 3:
Calcular el perímetro cuando se conoce la longitud de un lado

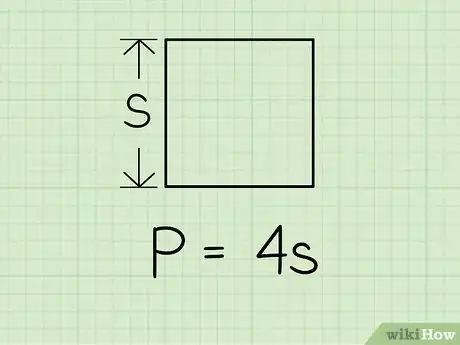
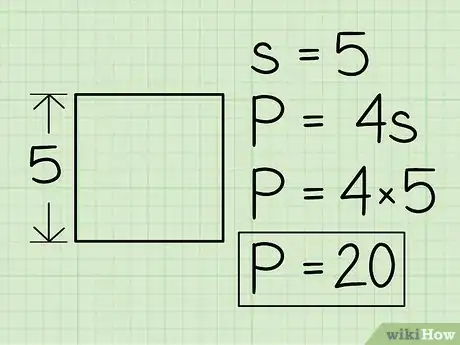
1
Recuerda la fórmula del perímetro de un cuadrado. Para un cuadrado cuya longitud es L, el perímetro es simplemente cuatro veces la longitud del lado: P=4L.
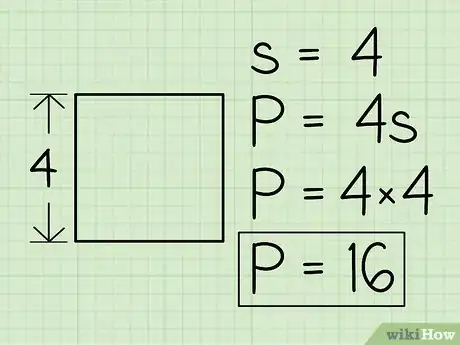
2
Determina la longitud de un lado y multiplícala por 4 para hallar el perímetro. Dependiendo de lo que debas hacer, es posible que necesites medir el lado con una regla o ver más información en la página para determinar la longitud del lado. Estos son algunos ejemplos para calcular el perímetro:
- Si un lado del cuadrado tiene una longitud de 4, entonces P = 4 * 4 o 16.
- Si un lado del cuadrado tiene una longitud de 6, entonces P = 4 * 6 o 36.

Método 2

Método 2 de 3:
Calcular el perímetro cuando se conoce el área

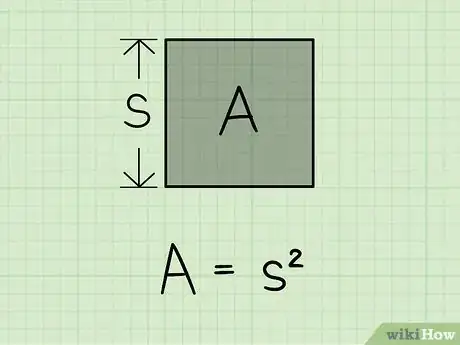
1
Conoce la fórmula para el área de un cuadrado. El área de cualquier rectángulo (recuerda, los cuadrados son rectángulos especiales) se define como su base por su altura.^{[3]
X
Fuente de investigación} Dado que la base y la altura de un cuadrado tienen la misma longitud, el área de un cuadrado con la misma longitud en todos los lados L es L*L o A = L².
2
Halla la raíz cuadrada del área. La raíz cuadrada del área te dará la longitud de uno de los lados del cuadrado. Para la mayoría de los números, necesitarás utilizar una calculadora para hallar la raíz cuadrada al escribir primero el valor del área, seguido del signo de la raíz cuadrada (√). ¡También puedes aprender a calcular una raíz cuadrada a mano!
- Si el área del cuadrado es 20, entonces la longitud del lado L =√20 o 4,472.
- Si el área del cuadrado es 25, entonces s = √25 o 5.
3
Multiplica la longitud del lado por 4 para hallar el perímetro. Toma la longitud del lado L que acabas de calcular y conéctalo en la fórmula del perímetro, P = 4L. ¡El resultado será el perímetro del cuadrado!
- Para un cuadrado con un área de 20 y una longitud de lado de 4,472, el perímetro P = 4 * 4,472 o 17,888.
- Para un cuadrado con un área de 25 y una longitud de lado de 5, P = 4 * 5 o 20.

Método 3

Método 3 de 3:
Calcular el perímetro de un cuadrado inscrito en un círculo de radio conocido

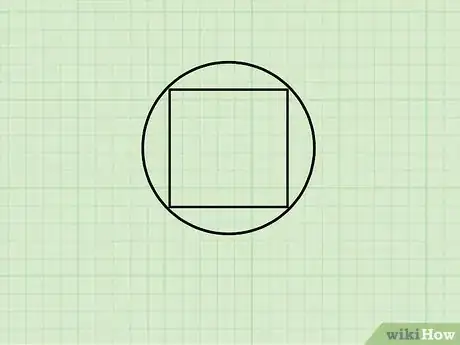
1
Entiende lo que es un cuadrado inscrito. A menudo, las formas inscritas se presentan fácilmente en ejemplos estandarizados tales como el GMAT y el GRE, de modo que es importante saber cuáles son. Un cuadrado inscrito en un círculo es un cuadrado dibujado dentro del círculo, de modo que los cuatro vértices (esquinas) yacen en el borde del círculo.^{[4]
X
Fuente de investigación}
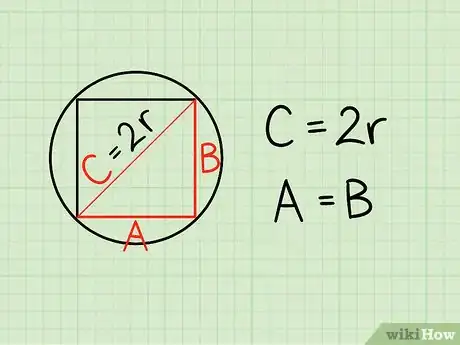
2
Reconoce la relación entre el radio del círculo y la longitud del lado del cuadrado. La distancia desde el centro de un cuadrado inscrito a cada una de sus esquinas es igual al radio del círculo. Para hallar la longitud de L, primero debemos imaginar que cortamos el cuadrado a la mitad por la diagonal para formar dos triángulos rectángulos. Cada uno de estos triángulos tendrán lados iguales a y b además de una hipotenusa c, la que sabemos que es igual a dos veces el radio del círculo o 2r.
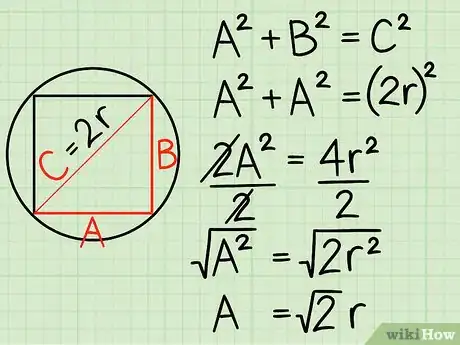
3
Utiliza el teorema de Pitágoras para hallar la longitud del lado del cuadrado. El teorema de Pitágoras determina que para cualquier triángulo rectángulo con lados a y b, y una hipotenusa c, a² + b² = c². ^{[5]
X
Fuente de investigación} Dado que los lados a y b son iguales (¡recuerda que aún lidiamos con un cuadrado!) y sabemos que c = 2r, podemos anotar la ecuación y simplificarla para hallar la longitud del lado de la siguiente manera:
- a² + a² = (2r)²"', ahora simplifica las expresiones:
- 2a² = 4(r)², ahora divide ambos lados entre 2:
- (a²) = 2(r)², ahora toma la raíz cuadrada de cada lado:
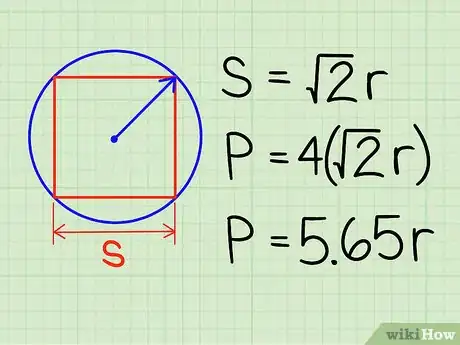
- a = √(2r). La longitud del lado s para el cuadrado inscrito = √(2r).
4
Multiplica la longitud del lado del cuadrado por cuatro para hallar el perímetro. En este caso, el perímetro del cuadrado P = 4√2r. ¡El perímetro de todo cuadrado inscrito en un círculo con radio r se define como P = 5,657r!
5
Resuelve una ecuación modelo. Considera un cuadrado inscrito en un círculo con un radio de 10. Eso significa que la diagonal de este cuadrado = 2(10) o 20. Utilizando el teorema de Pitágoras, sabemos que 2(a²) = 20², así que 2a² = 400. Ahora dividamos ambos lados a la mitad para hallar a² = 200. Luego toma la raíz cuadrada de cada lado para descubrir que a = 14,142. Multiplícalo por 4 y hallarás el perímetro del cuadrado: P = 56,57.
- Ten en cuenta que podrías haber hallado lo mismo con solo multiplicar el radio (10) por 5,657. 10 * 5,567 = 56,57, pero eso podría ser difícil de recordar durante un examen, así que es mejor memorizar el proceso que utilizamos en este artículo para hallar la respuesta.