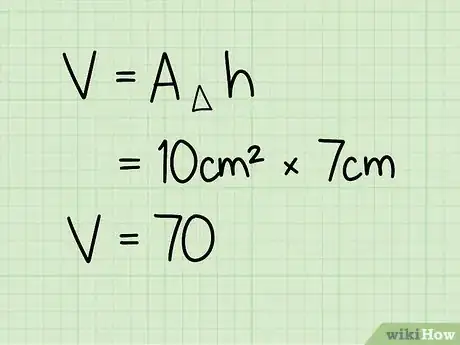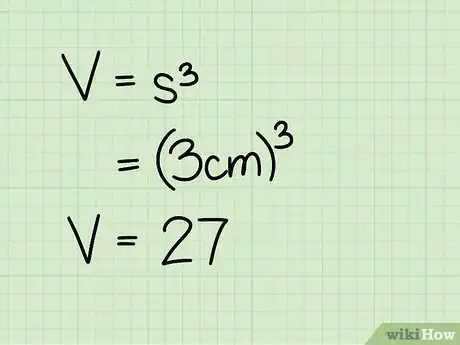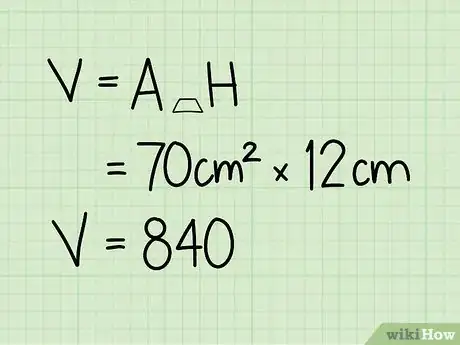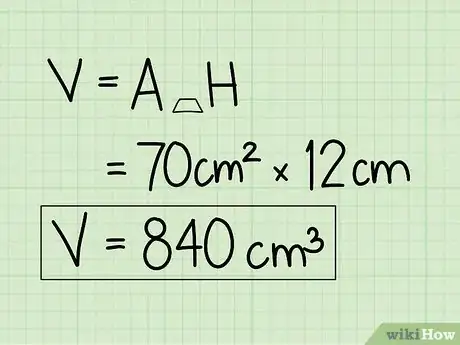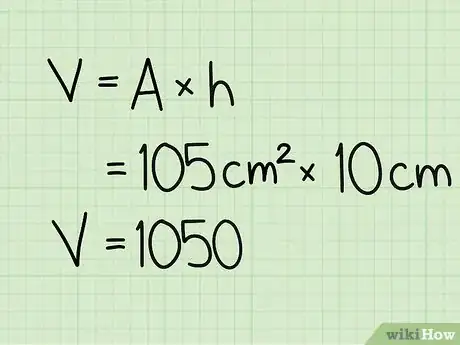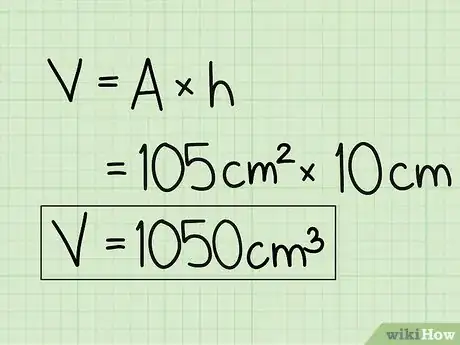Cómo calcular el volumen de un prisma

Un prisma es una figura geométrica sólida con dos lados opuestos idénticos y compuesta solo de superficies planas. Cada prisma obtiene su nombre de la forma de su base, así que a un prisma con una base triangular se le conoce como "prisma triangular". Para encontrar el volumen de un prisma, solo debes calcular el área de su base y multiplicarla por su altura. Calcular el área de la base puede ser la parte complicada. Aquí te enseñamos cómo calcular el volumen de una variedad de prismas. El volumen y la capacidad son similares, pero aquí aprenderás a calcular el volumen de los prismas.

Método 1
Método 1 de 5:
Calcular el volumen de un prisma triangular

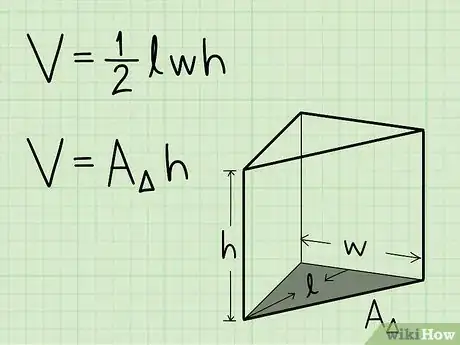
  1. Imagen titulada Calculate the Volume of a Prism Step 1
    1
    Anota la fórmula para encontrar el volumen de un prisma triangular. La fórmula es simplemente V = 1/2 x longitud x anchura x altura. Sin embargo, separaremos esta fórmula para utilizar la fórmula V = área de la base x altura. Puedes encontrar el área de la base utilizando la fórmula para el área del triángulo. Multiplica ½ por la longitud y la anchura de la base.
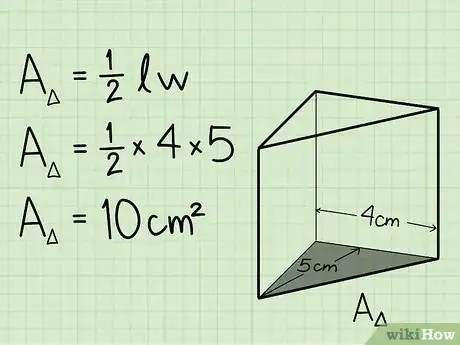
  2. Imagen titulada Calculate the Volume of a Prism Step 2
    2
    Encuentra el área de la base. Para calcular el volumen de un prisma triangular, primero deberás encontrar el área de su base triangular. Encuentra el área de la base del prisma multiplicando ½ por la base del triángulo por la altura del mismo.[1]
    • Ejemplo: si la altura del triángulo es de 5 cm y la base es de 4cm, entonces el área de la base triangular será 1/2 x 5 cm x 4 cm, lo cual da 10 cm2.
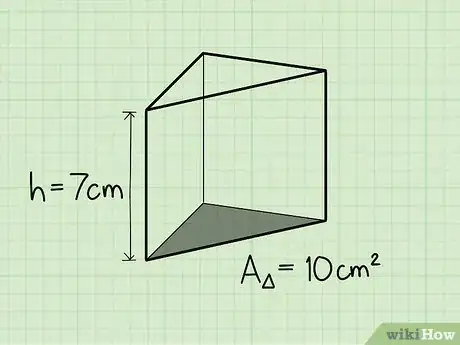
  3. Imagen titulada Calculate the Volume of a Prism Step 3
    3
    Encuentra la altura. Digamos que la altura de este prisma triangular es de 7 cm.
  4. Imagen titulada Calculate the Volume of a Prism Step 4
    4
    Multiplica el área de la base triangular por la altura del prisma. Simplemente multiplica el área de tu base por la altura. Después de multiplicar base por altura, tendrás el volumen del prisma triangular.
    • Ejemplo:10 cm2 x 7 cm = 70 cm3
  5. Imagen titulada Calculate the Volume of a Prism Step 5
    5
    Escribe tu respuesta en unidades cúbicas. Siempre deberás utilizar unidades cúbicas al calcular volumen porque estás trabajando con objetos tridimensionales. Tu respuesta final será 70 cm.3

Método 2
Método 2 de 5:
Calcular el volumen de un cubo

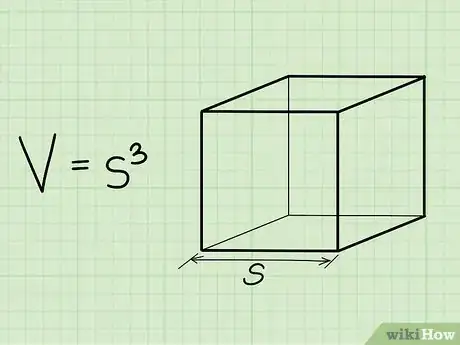
  1. Imagen titulada Calculate the Volume of a Prism Step 6
    1
    Anota la fórmula para encontrar el volumen de un cubo. La fórmula es simplemente V = lado3. Un cubo es un prisma que tiene sus tres lados iguales.[2]
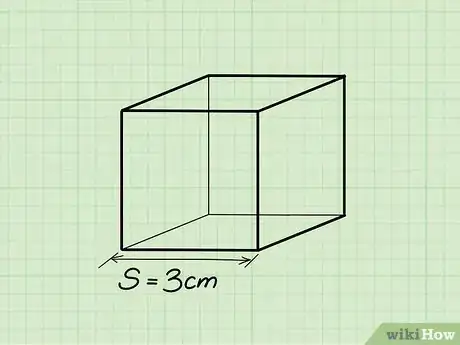
  2. Imagen titulada Calculate the Volume of a Prism Step 7
    2
    Encuentra la longitud de uno de los lados del cubo. Todos sus lados son iguales, así que no importa cuál elijas.
    • Ejemplo: Longitud = 3 cm.
  3. Imagen titulada Calculate the Volume of a Prism Step 8
    3
    Sácale el cubo. Para sacar el cubo de un número, simplemente multiplícalo por sí mismo dos veces. El cubo de "a" es "a x a x a," por ejemplo. Debido a que todos los lados del cubo tienen la misma longitud, no tendrás que encontrar el área de la base y multiplicarla por la altura. Multiplicar dos lados cualesquiera del cubo te dará el área de la base, y un tercer lado cualquiera representará la altura. Puedes seguir considerándolo como multiplicar la longitud, la anchura y la altura solo que resulta las tres que tienen el mismo valor.
    • Ejemplo: 3 cm3 = 3 cm * 3 cm * 3 cm = 27 cm3
  4. Imagen titulada Calculate the Volume of a Prism Step 9
    4
    Escribe tu respuesta en unidades cúbicas. No olvides anotar tu respuesta final en unidades cúbicas. El resultado final es 125 cm3.

Método 3
Método 3 de 5:
Calcular el volumen de un prisma rectangular

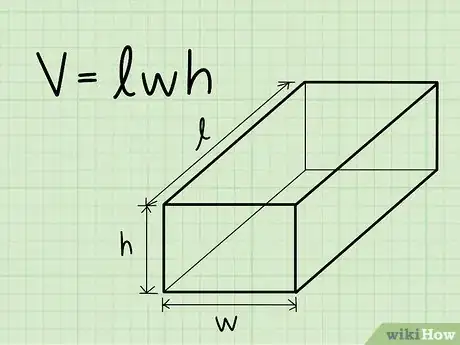
  1. Imagen titulada Calculate the Volume of a Prism Step 10
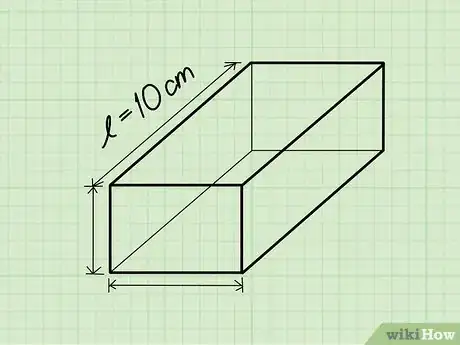
    1
    Anota la fórmula para encontrar el volumen de un prisma rectangular. La fórmula es simplemente V = longitud * anchura * altura. Un prisma rectangular es un prisma con una base rectangular.
  2. Imagen titulada Calculate the Volume of a Prism Step 11
    2
    Encuentra la longitud. La longitud es el lado más largo de la superficie plana del rectángulo en la parte superior o inferior del prisma rectangular.
    • Ejemplo: Longitud = 10 cm.
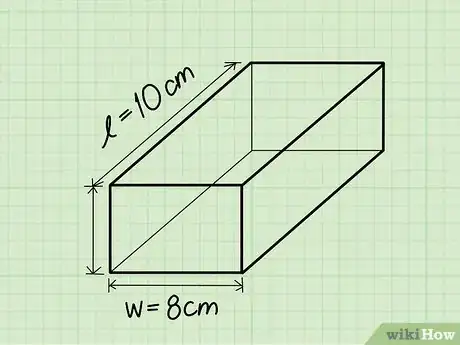
  3. Imagen titulada Calculate the Volume of a Prism Step 12
    3
    Encuentra la anchura. La anchura de un prisma rectangular es el lado más corto de la superficie plana del rectángulo en la parte superior o inferior de la figura.
    • Ejemplo: Anchura = 8 cm.
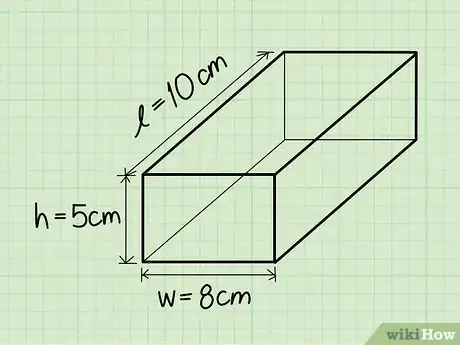
  4. Imagen titulada Calculate the Volume of a Prism Step 13
    4
    Encuentra la altura. La altura es la parte del prisma rectangular que se eleva. Puedes imaginar la altura del prisma rectangular como la parte que estira un rectángulo hacia arriba y lo convierte en un objeto tridimensional.
    • Ejemplo: Altura = 5 cm.
  5. Imagen titulada Calculate the Volume of a Prism Step 14
    5
    Multiplica la longitud por la anchura y la altura. Puedes multiplicarlas en cualquier orden y obtendrás el mismo resultado. Con este método puedes sacar primero el área de la base rectangular (10 x 8) y luego multiplicar ese resultado por la altura (5). Pero para encontrar el volumen de este tipo de prismas puedes multiplicar esos valores en cualquier orden.
    • Ejemplo: 10 cm * 8 cm * 5 cm = 400 cm3
  6. Imagen titulada Calculate the Volume of a Prism Step 15
    6
    Escribe tu respuesta en unidades cúbicas. La respuesta final es 400 cm.3

Método 4
Método 4 de 5:
Calcular el volumen de un prisma trapezoidal

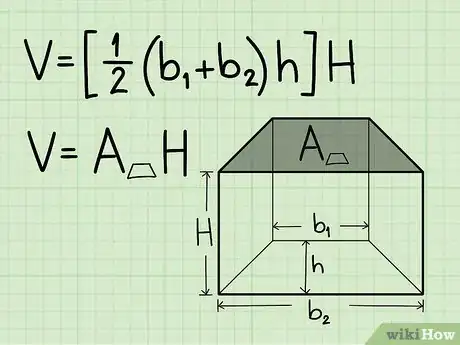
  1. Imagen titulada Calculate the Volume of a Prism Step 16
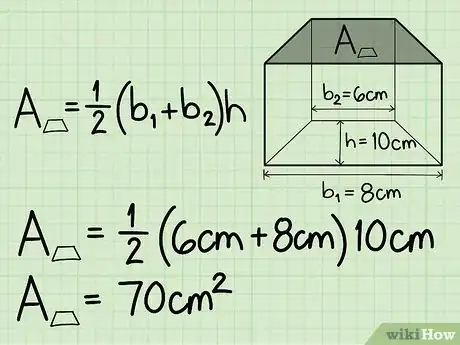
    1
    Escribe la fórmula para calcular el volumen de un prisma trapezoidal. La fórmula es: V = [1/2 x (base1 + base2) x altura] x altura del prisma. Deberás utilizar la primera parte de esta fórmula para encontrar el área de la base trapezoidal del prisma antes de que continúes.[3]
  2. Imagen titulada Calculate the Volume of a Prism Step 17
    2
    Encuentra el área de la base trapezoidal. Para hacer esto, simplemente inserta los valores de las dos bases y de la altura de la base trapezoidal en la fórmula.
    • Digamos que base 1 = 8 cm, base 2 = 6 cm, y la altura = 10 cm.
    • Ejemplo: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm2.
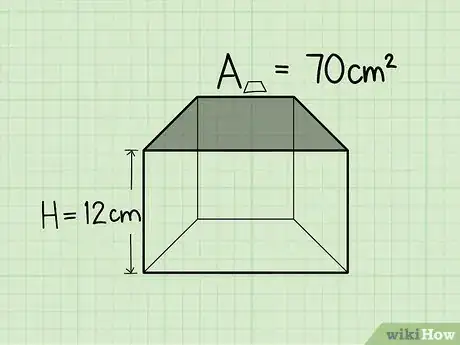
  3. Imagen titulada Calculate the Volume of a Prism Step 18
    3
    Encuentra la altura del prisma trapezoidal. Digamos que la altura del trapezoide es de 12 cm.
  4. Imagen titulada Calculate the Volume of a Prism Step 19
    4
    Multiplica el área de la base por la altura del prisma. Para calcular el volumen de tu prisma trapezoidal, solo deberás multiplicar el área de la base por la altura del prisma.
    • 80 cm2 x 12 cm = 960 cm3.
  5. Imagen titulada Calculate the Volume of a Prism Step 20
    5
    Escribe tu respuesta en unidades cúbicas. El resultado final es 960 cm3

Método 5
Método 5 de 5:
Calcular el volumen de un prisma pentagonal regular

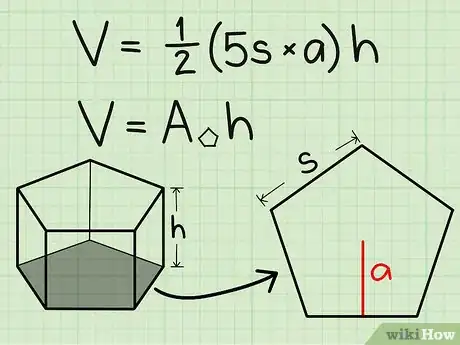
  1. Imagen titulada Calculate the Volume of a Prism Step 21
    1
    Escribe la fórmula para encontrar el volumen de un prisma pentagonal regular. La fórmula es V = [1/2 x 5 x lado x apotema x altura del prisma. Puedes utilizar la primera parte de la fórmula para encontrar el área de la base pentagonal. Puedes ver esto como si estuvieras encontrando el área de los cinco triángulos que forman tu polígono regular. Un lado es simplemente la anchura de un triángulo y la apotema es la altura de este. Estarás multiplicando por ½ porque eso es parte de la fórmula para encontrar el área de un triángulo y luego multiplicarás por 5 ya que el pentágono está compuesto por 5 triángulos.[4]
    • Si no te dan la apotema, consulta esta guía sobre cómo calcular la apotema de un polígono regular.
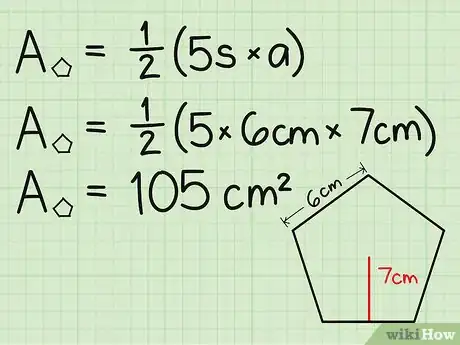
  2. Imagen titulada Calculate the Volume of a Prism Step 22
    2
    Encuentra el área de tu base pentagonal. Digamos que la longitud de un lado es de 6 cm y la longitud de la apotema es de 7 cm. Tan solo inserta estos valores en la fórmula:
    • A = 1/2 x 5 x lado x apotema
    • A = 1/2 x 5 x 6 cm x 7 cm = 105 cm2
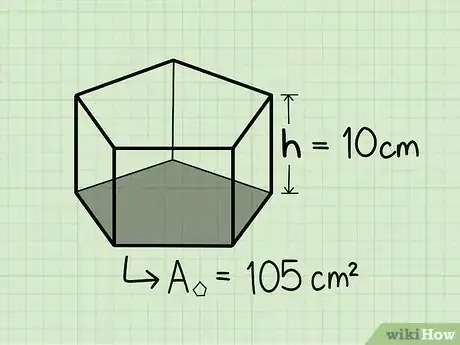
  3. Imagen titulada Calculate the Volume of a Prism Step 23
    3
    Encuentra la altura. Digamos que la altura de tu figura es de 10 cm.
  4. Imagen titulada Calculate the Volume of a Prism Step 24
    4
    Multiplica el área de tu base pentagonal por la altura. Tan solo multiplica el área de tu base pentagonal, 105 cm2, por la altura, 10 cm, para encontrar el volumen de tu prisma pentagonal.
    • 105 cm2 x 10 cm = 1050 cm3
  5. Imagen titulada Calculate the Volume of a Prism Step 25
    5
    Escribe tu respuesta en unidades cúbicas. Tu respuesta final será 1050 cm3.

Consejos

  • No confundas la base de la figura bidimensional con la base de la figura tridimensional. La base de la figura tridimensional será la cara bidimensional (la cual se encuentra dos veces en el prisma, arriba y abajo). Esta base bidimensional tendrá a su vez una base, una medida unidimensional que te servirá para encontrar su área.

wikiHows relacionados

calcular el radio de un círculo
Cómo
calcular el radio de un círculo
calcular la circunferencia de un círculo
Cómo
calcular la circunferencia de un círculo
encontrar el vértice de una ecuación cuadrática
Cómo
encontrar el vértice de una ecuación cuadrática
sacar el área de un cuadrilátero
Cómo
sacar el área de un cuadrilátero
calcular ángulos
Cómo
calcular ángulos
calcular la circunferencia
Cómo
calcular la circunferencia
encontrar el radio de una esfera
Cómo
encontrar el radio de una esfera
sacar el volumen de un cubo
Cómo
sacar el volumen de un cubo
calcular cuántas diagonales tiene un polígono
Cómo
calcular cuántas diagonales tiene un polígono
medir un ángulo sin usar un transportador
Cómo
medir un ángulo sin usar un transportador
encontrar la magnitud de un vector
Cómo
encontrar la magnitud de un vector
sacar el angulo de un triangulo
Cómo
sacar el angulo de un triangulo
calcular metros cuadrados
Cómo
calcular metros cuadrados
dibujar un hexágono
Cómo
dibujar un hexágono

Referencias

  1. ↑ http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i22/bk7_22i6.htm
  2. ↑ http://www.basic-mathematics.com/volume-of-a-cube.html
  3. ↑ http://www.mathgoodies.com/lessons/vol1/area_trapezoid.html
  4. ↑ http://www.wikicalculator.com/formula_calculator/Volume-Area-of-Pentagonal-Prism-130.htm

Acerca de este wikiHow

wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 15 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo. Este artículo ha sido visto 492 909 veces.
Categorías: Geometría