Cómo calcular el volumen dentro de una caja

Ya sea que necesites enviar un paquete por correo o aprobar tu siguiente examen, encontrar el volumen de una caja es fácil. El volumen es la medida de qué tan grande es un objeto en tres dimensiones, así que el volumen de una caja mide cuánto espacio hay dentro de ella. Para encontrarlo, necesitas hacer algunas mediciones simples de la longitud, el ancho y la altura, y luego multiplicarlas.

Método 1

Método 1 de 2:
Calcular el volumen de cajas rectangulares

1
Entiende que el volumen de un rectángulo es igual a su longitud x ancho x altura. Si la caja es un prisma rectangular o un cubo, la única información que necesitas es la longitud, el ancho y la altura de la caja. Luego puedes multiplicarlos para obtener el volumen. Esta fórmula a menudo se abrevia como V = l x a x h.^{[1]
X
Fuente de investigación}
- Pregunta de ejemplo: "Si tengo una caja con una longitud de 10 cm, un ancho de 4 cm y una altura de 5 cm, ¿cuál es el volumen de la caja?".
- V = l x a x h
- V = 10 cm x 4 cm x 5 cm
- V = 200 cm³
- La "altura" puede ser reemplazada por la "profundidad". Por ejemplo, "La caja tiene una longitud de 10 cm, un ancho de 4 cm y 5 cm de profundidad".^{[2]
  X
  Fuente de investigación}
2
Mide la longitud de una caja. Si miras la caja hacia abajo, la parte superior parece ser un rectángulo plano. La longitud es el lado más largo de este rectángulo. Anota este número como la "longitud".^{[3]
X
Fuente de investigación}
- Asegúrate de usar la misma medida para cada lado. Si mides un lado en pulgadas, necesitas medir todos en pulgadas.
3
Mide el ancho de la caja que está junto a la longitud. El ancho de la caja es el otro borde que está junto a la longitud. Si ves un lado de la caja, el ancho es el lado que forma una "L" con la longitud. Anota esta medida como el "ancho".^{[4]
X
Fuente de investigación}
- El ancho siempre es el lado más corto.
4
Mide la altura de la caja. Este es el último lado que no has medido, y es la distancia desde la parte superior de la caja al suelo. Anota esta medida como la "altura".
- Dependiendo de cómo esté colocada la caja, el lado al que llames "altura" o "longitud" podría ser diferente. Sin embargo, no importa a qué lado le llames longitud, solo que midas 3 lados diferentes.
5
Multiplica los tres lados. Recuerda, la ecuación para el volumen es V = longitud x ancho x altura, así que simplemente multiplica los tres lados para obtener el volumen. Asegúrate de incluir también las unidades que usaste para medir, para que no te olvides lo que los números significan.^{[5]
X
Fuente de investigación}

CONSEJO DE ESPECIALISTA

Grace Imson, MA
Instructora de matemáticas en City College de San Francisco
Grace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión de la Universidad de Saint Louis.

Grace Imson, MA
Instructora de matemáticas en City College de San Francisco

Asegúrate de que todas las unidades sean las mismas antes de multiplicar. Los problemas de matemáticas complicados darán una unidad de medida diferente para la longitud, el ancho y la altura de la caja. No podrás multiplicar las dimensiones para hallar el volumen hasta que todas tengan la misma unidad.
6
Añade las "unidades³" al volumen. El volumen es una medición, pero si no conoces el sistema de medida, el número no tendrá sentido. La forma correcta de escribir el volumen completo es con el tipo de medida al cubo. Por ejemplo, si mides todos los lados en pulgadas, la respuesta final estaría en "pulgadas³."^{[6]
X
Fuente de investigación}
- Pregunta de ejemplo: "Si tengo una caja con una longitud de 2 pies, un ancho de 1 pie y una altura de 3 pies, ¿cuál es el volumen de la caja?".
- V = l x a x h
- V = 2 pies x 1 pie x 4 pies
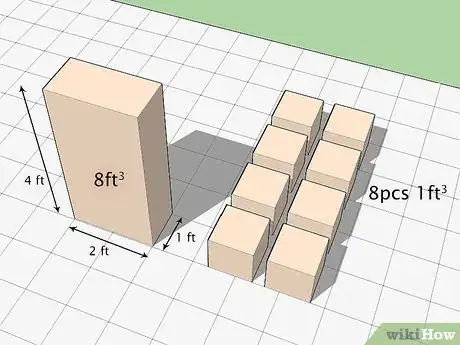
- Volumen = 8 pies³
- Nota: esto se debe a que el volumen te dice cuántos cubos pequeños podrías colocar en la caja. En el ejemplo anterior, esto significa que podrías colocar 8 cubos de 1 pie en la caja.

Método 2

Método 2 de 2:
Calcular cajas de diferentes formas

1
Encuentra el volumen de cilindros. Los cilindros son tubos, donde la parte superior y la parte inferior son círculos. Para encontrar el volumen de un cilindro, usa la ecuación V = pi x r² x a. Donde pi = 3,14, r es el radio del círculo superior y a es la altura.^{[7]
X
Fuente de investigación}
- Para encontrar el volumen de un cono, o una pirámide con un círculo en la parte inferior, usa la misma ecuación multiplicada por 1/3. Así que, el volumen de un cono = 1/3(pi x r² x a)
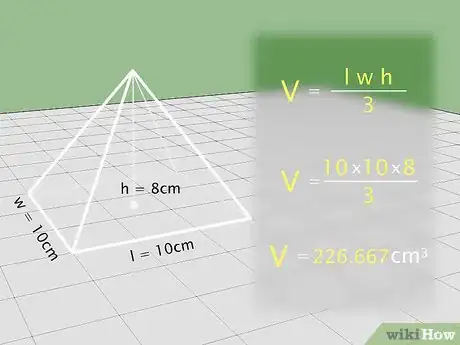
2
Encuentra el volumen de una pirámide. Las pirámides tienen un lado, o base, y todos los otros lados se encuentran en un punto. Para encontrar el volumen, multiplica el área de la base por la altura y luego multiplica eso por la fracción 1/3. Así, el volumen de una pirámide = 1/3(base x altura).^{[8]
X
Fuente de investigación}
- La mayoría de las pirámides tienen bases cuadradas o rectangulares. El área de una base se encuentra multiplicando la longitud de la base por el ancho.
3
Suma el volumen de las partes para encontrar el volumen de formas complicadas. Por ejemplo, si necesitas encontrar el volumen de una caja con forma de "L", hay más de tres lados para medir. Sin embargo, si ves la caja como dos cajas más pequeñas, puedes encontrar el volumen de cada caja más pequeña y sumarlos para obtener el volumen final. Con la caja con forma de "L", por ejemplo, puedes ver la línea vertical como una caja rectangular y la línea horizontal de la parte inferior como una caja cuadrada.^{[9]
X
Fuente de investigación}
- Aunque se vuelve complicado, hay muchas formas de encontrar el volumen para cualquier forma.