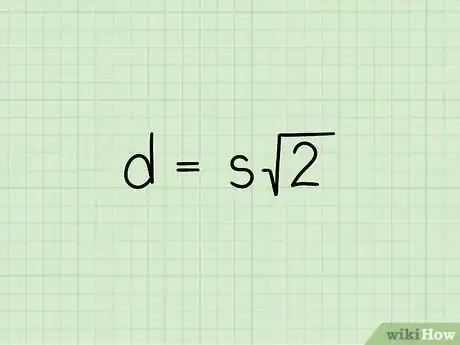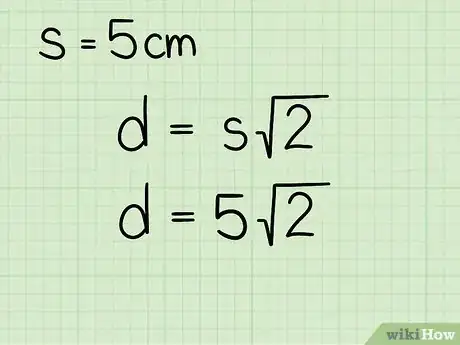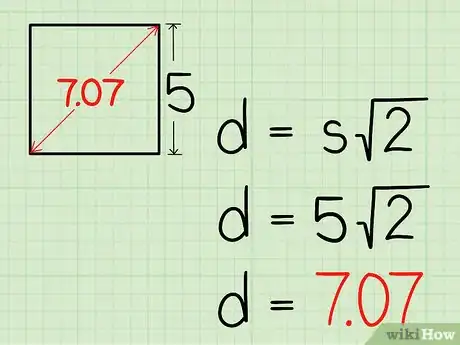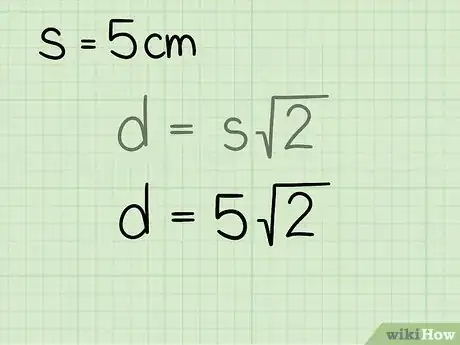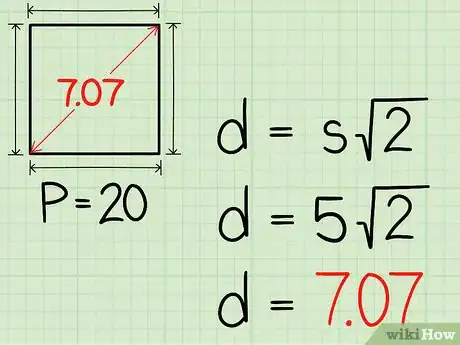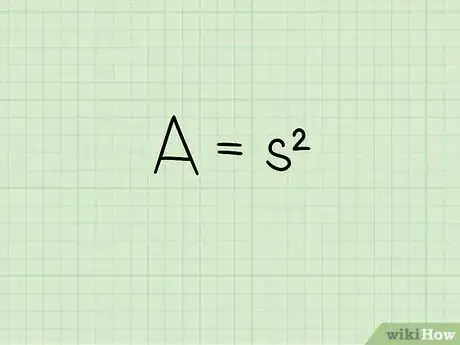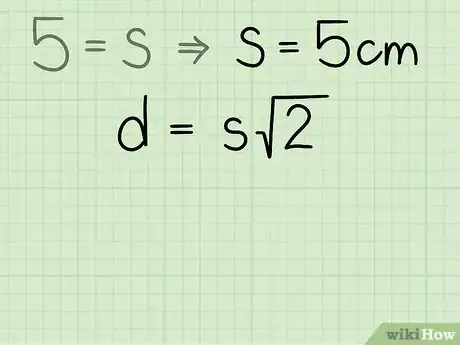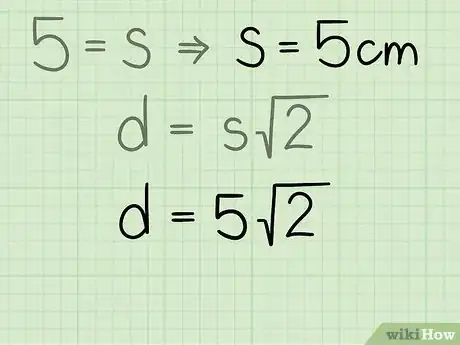Cómo calcular la diagonal de un cuadrado

Coescrito por David Jia

La diagonal de un cuadrado es la línea que se extiende desde una esquina hasta la esquina opuesta. Puedes usar la fórmula $d=l{\sqrt {2}}$ para encontrar la diagonal de un cuadrado, en donde $l$ es igual a la longitud de uno de los lados del cuadrado. Sin embargo, en ocasiones se te podría dar otro valor (como el perímetro o el área del cuadrado) a partir del cual debas encontrar la longitud de la diagonal, en cuyo caso será necesario emplear primero otras fórmulas. De esta forma, podrás encontrar la longitud de los lados del cuadrado antes de emplear la fórmula para la diagonal.

Método 1

Método 1 de 3:
Si sabes la longitud de uno de los lados

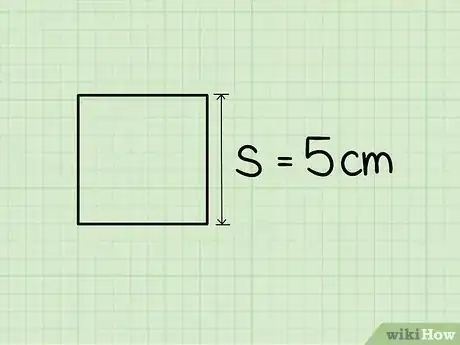
1
Encuentra la longitud de uno de los lados del cuadrado. Es probable que se te dé esta información. Si el cuadrado con el que estés trabajando es real, puedes encontrar la longitud usando una regla o una cinta métrica. Los cuatro lados de un cuadrado son iguales, por lo que puedes medir cualquier lado. No podrás usar este método si no tienes la longitud de uno de los lados del cuadrado.
- Por ejemplo, podrías tener que encontrar la longitud de la diagonal de un cuadrado cuyos lados midan 5 cm.
2
Establece la fórmula $d=l{\sqrt {2}}$ . Aquí, $d$ $d$ es igual a la longitud de la diagonal y $l$ $l$ es igual a un lado del cuadrado.^{[1]
X
Fuente de investigación}
- Esta fórmula se obtiene del teorema de Pitágoras ( $a^{2}+b^{2}=c^{2})$ . La diagonal de un cuadrado lo divide en dos triángulos rectángulos congruentes, por lo que la longitud de los lados del cuadrado puede usarse para encontrar la longitud de la diagonal (es decir, la hipotenusa del triángulo rectángulo).
3
Reemplaza la longitud del lado en la fórmula. Ten cuidado de reemplazar la variable $l$ $l$ .
- Por ejemplo, si el lado del cuadrado mide 5 cm, debes configurar la fórmula de la siguiente forma:
  $d=5{\sqrt {2}}$
4
Multiplica la longitud de uno de los lados por ${\sqrt {2}}$ . De esta forma, obtendrás la longitud de la diagonal. Lo mejor es realizar esta operación en una calculadora para que el resultado que obtengas sea más preciso. En caso de que no tengas una, puedes redondear ${\sqrt {2}}$ ${\sqrt {2}}$ a 1,414.
- Por ejemplo, para calcular la diagonal de un cuadrado de 5 cm por lado, así se vería la fórmula:
  $d=5{\sqrt {2}}$
  $d=7,07$
  Por tanto, la diagonal del cuadrado mide 7,07 cm.
Anuncio

Método 2

Método 2 de 3:
Si sabes el perímetro

1
Establece la fórmula para el perímetro de un cuadrado. Esta es $P=4l$ $P=4l$ , donde $P$ $P$ equivale al perímetro del cuadrado y $l$ $l$ equivale a la longitud de uno de los lados de este.^{[2]
X
Fuente de investigación}
- Solo puedes usar este método si sabes el perímetro del cuadrado.
- Si quieres encontrar la longitud de la diagonal, primero debes encontrar la longitud de uno de los lados del cuadrado. Por tanto, establece la fórmula para el perímetro y luego encuentra la variable $l$ .
2
Reemplaza la longitud del perímetro en la fórmula. Ten cuidado de reemplazar la variable $P$ $P$ .
- Por ejemplo, si el cuadrado tiene un perímetro de 20 cm, así se verá la fórmula:
  $20=4l$
3
Encuentra $l$ . Para ello, debes dividir cada uno de los lados de la ecuación entre 4. De esta forma, obtendrás la longitud de uno de los lados del cuadrado.
- Por ejemplo:
  $20=4l$
  ${\frac {20}{4}}={\frac {4l}{4}}$
  $5=l$
4
Establece la fórmula $d=l{\sqrt {2}}$ . Aquí, $d$ $d$ equivale a la longitud de la diagonal y $l$ $l$ equivale a la longitud de un lado del cuadrado.^{[3]
X
Fuente de investigación}
- Esta fórmula se obtiene del teorema de Pitágoras ( $a^{2}+b^{2}=c^{2})$ . La diagonal de un cuadrado lo divide en dos triángulos rectángulos congruentes, por lo que la longitud de los lados del cuadrado puede usarse para encontrar la longitud de la diagonal (es decir, la hipotenusa del triángulo rectángulo).
5
Reemplaza la longitud del lado en la fórmula. Ten cuidado de reemplazar la variable $l$ $l$ .
- Por ejemplo, si el lado del cuadrado mide 5 cm, así se verá la fórmula:
  $d=5{\sqrt {2}}$
6
Multiplica el lado del cuadrado por ${\sqrt {2}}$ . De esta forma, obtendrás la longitud de la diagonal. Lo mejor es realizar esta operación en una calculadora para que el resultado que obtengas sea más preciso. En caso de que no tengas una, puedes redondear ${\sqrt {2}}$ ${\sqrt {2}}$ a 1,414.
- Por ejemplo, para calcular la diagonal de un cuadrado de 5 cm por lado, así se vería la fórmula:
  $d=5{\sqrt {2}}$
  $d=7,07$
  Por tanto, la diagonal del cuadrado mide 7,07 cm.
Anuncio

Método 3

Método 3 de 3:
Si sabes el área

1
Establece la fórmula para el área de un cuadrado. La fórmula es $A=l^{2}$ $A=l^{{2}}$ , donde $A$ $A$ equivale al área del cuadrado y $l$ $l$ equivale a la longitud de un lado.^{[4]
X
Fuente de investigación}
- Solo podrás usar este método si sabes el área del cuadrado.
- Si quieres encontrar la longitud de la diagonal, primero debes encontrar la longitud de uno de los lados del cuadrado. Por tanto, debes establecer la fórmula para el área y luego encontrar la variable $l$ .
2
Reemplaza el valor del área en la fórmula. Ten cuidado de reemplazar la variable $A$ $A$ .
- Por ejemplo, si el cuadrado tiene un área de 25 centímetros cuadrados, así se verá la fórmula:
  $25=l^{2}$
3
Encuentra $l$ . Para ello, debes obtener la raíz cuadrada del área, lo cual te dará la longitud de uno de los lados del cuadrado. Debes usar una calculadora para encontrar la raíz cuadrada. En caso de que necesites ayuda para calcularla a mano, lee el artículo Cómo calcular una raíz cuadrada.
- Por ejemplo:
  $25=l^{2}$
  ${\sqrt {25}}={\sqrt {l^{2}}}$
  $5=l$
4
Establece la fórmula $d=l{\sqrt {2}}$ . Aquí, $d$ $d$ equivale a la longitud de la diagonal y $l$ $l$ equivale a un lado del cuadrado.^{[5]
X
Fuente de investigación}
- Esta fórmula se obtiene del teorema de Pitágoras ( $a^{2}+b^{2}=c^{2})$ . La diagonal de un cuadrado lo divide en dos triángulos rectángulos congruentes, por lo que la longitud de los lados del cuadrado puede usarse para encontrar la longitud de la diagonal (es decir, la hipotenusa del triángulo rectángulo).
5
Reemplaza la longitud de un lado del cuadrado en la fórmula. Ten cuidado de reemplazar la variable $l$ $l$ .
- Por ejemplo, si el lado del cuadrado mide 5 cm, así se verá la fórmula:
  $d=5{\sqrt {2}}$
6
Multiplica el lado del cuadrado por ${\sqrt {2}}$ . Así obtendrás la longitud de la diagonal. Lo mejor es realizar esta operación en una calculadora para que el resultado que obtengas sea más preciso. En caso de que no tengas una, puedes redondear ${\sqrt {2}}$ ${\sqrt {2}}$ a 1,414.
- Por ejemplo, para calcular la diagonal de un cuadrado de 5 cm por lado, así se vería la fórmula:
  $d=5{\sqrt {2}}$
  $d=7,07$
  Por tanto, la diagonal del cuadrado mide 7,07 cm.
Anuncio