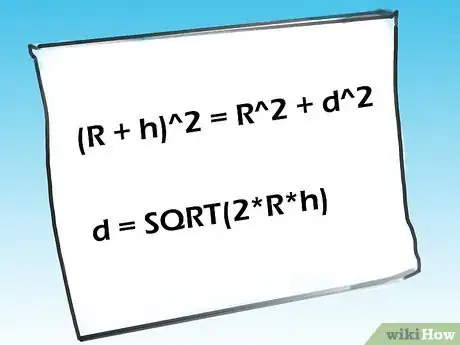Cómo calcular la distancia del horizonte

Información del autor

¿Alguna vez has visto el sol desaparecer en el horizonte y te has preguntado, "¿Qué tan lejos está el horizonte desde dónde estoy?" Si puedes medir qué tan arriba están tus ojos del nivel del mar, entonces podrás calcular la distancia entre el horizonte y tú de la siguiente manera

Método 1

Método 1 de 3:
Calcular la distancia usando la geometría

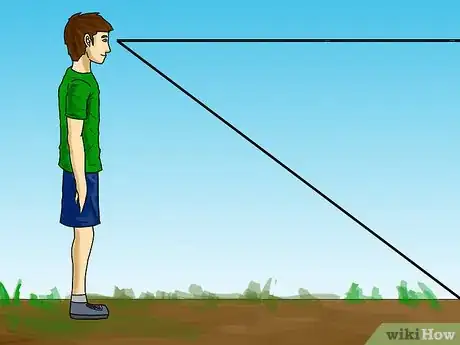
1
Mide la "altura de los ojos." Mide la longitud entre el suelo y los ojos en metros o pies. Una forma de calcularla es medir la distancia entre los ojos y la parte superior de tu cabeza. Réstale a ese valor tu altura total, y lo que quede será la distancia entre los ojos y la superficie en donde estés parado. Si estás parado exactamente sobre el nivel del mar con la parte inferior de tus pies en el agua, entonces esa será la única medida que necesitarás.
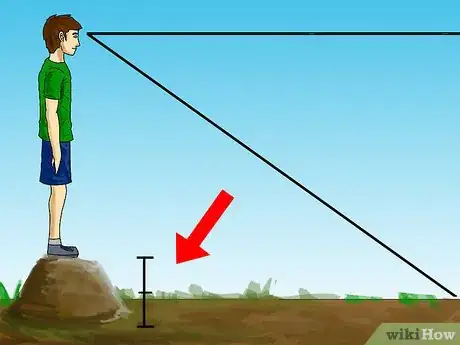
2
Agrega la "elevación local" si estás de pie sobre una superficie elevada, como una colina, edificio o barco. ¿A cuántos metros o pies por encima del horizonte verdadero te encuentras? ¿1 metro? ¿4.000 pies? Suma el número a la altura de los ojos (en las mismas unidades, por supuesto).
3
Multiplica por 13 metros si tomaste la medida en metros, o multiplica por 1.5 pies si tomaste la medida en pies.
4
Saca la raíz cuadrada para encontrar la respuesta. Si usaste metros, la respuesta será en kilómetros, y si usaste pies, la respuesta será en millas. La distancia calculada es una línea recta desde los ojos hasta el horizonte.
- La distancia real que te tomaría llegar al horizonte es más larga debido a la curvatura de la superficie y las irregularidades de la tierra. Continúa con el siguiente método de abajo para ver una fórmula más exacta (pero complicada).
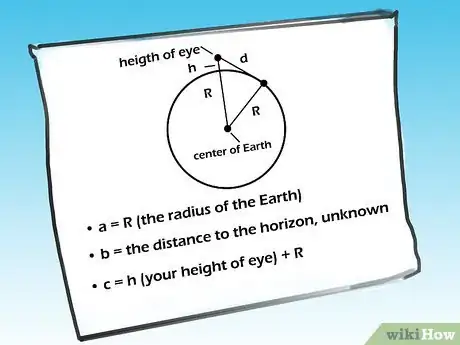
5
Entiende cómo funciona este cálculo. Se basa en un triángulo formado por el punto de observación (tus ojos), el verdadero punto del horizonte (el punto que observas) y el centro de la Tierra.
- Al conocer el radio de la Tierra y la medida de la altura de los ojos y la elevación local, queda solo la distancia entre los ojos y el horizonte como valores desconocidos. Dado que los lados del triángulo que se unen en el horizonte en realidad forman un ángulo recto, puedes usar el teorema de Pitágoras (bueno de² + b² = c²) como base para este cálculo, donde:
  
  • a = R (el radio de la Tierra)
  
  • b = la distancia al horizonte, desconocida
  
  • c = h (la altura de los ojos) + R
Anuncio

Método 2

Método 2 de 3:
Calcular la distancia usando trigonometría

1
Calcula la distancia real que tendrás que atravesar para llegar al horizonte mediante la siguiente fórmula.
- d = R * arccos(R/(R + h)), donde
  
  • d = distancia al horizonte
  
  • R = radio de la Tierra
  
  • h = altura de los ojos
2
Aumenta R en un 20% para compensar la distorsión de la refracción de los rayos de luz y para llegar a una medida más exacta. El horizonte geométricamente calculado con el método en este artículo no puede ser el mismo que el horizonte óptico, que es lo que el ojo ve realmente. ¿Por qué es esto?
- La atmósfera curva (refracta) la luz que viaja horizontalmente. Lo que esto significa es que por lo general un rayo de luz es capaz de seguir ligeramente la curvatura de la tierra, de modo que el horizonte óptico está un poco más lejos que el horizonte geométrico.
- Lamentablemente, la refracción debido a la atmósfera no es ni constante ni previsible, ya que depende de la variación de la temperatura con la altura. Por tanto, no hay una forma sencilla de añadir una corrección a la fórmula para el horizonte geométrico, aunque puedes lograr una corrección "promedio" asumiendo un radio de la Tierra, que sea un poco mayor que el radio verdadero.
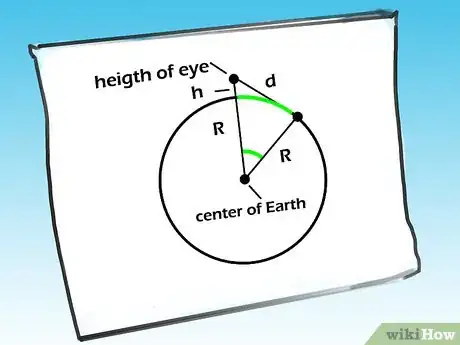
3
Entiende cómo funciona este cálculo. Esto calculará la longitud de la línea curva que sigue desde los pies al horizonte verdadero (se muestra en verde en esta imagen). Ahora, la porción arccos(R/(R+h)) se refiere al ángulo que se hace en el centro de la Tierra por la línea que va desde el horizonte verdadero hacia el centro y la línea que va desde ti hasta el centro. Con este punto de vista, lo multiplicas por R para obtener la "longitud del arco", que, en este caso, es la distancia que buscas.

Anuncio

Método 3

Método 3 de 3:
Cálculos geométricos alternativos

1
Asume una superficie plana o el océano. Este método es una versión más simple de la primera serie de instrucciones que se presentan en este artículo, y se aplica solamente en pies y millas.
2
Resuelve la distancia en millas colocando la altura de los ojos en pies (h) en la fórmula. La fórmula que utilizarás es d = 1.2246* SQRT(h)
3
Deduce la fórmula del teorema de Pitágoras. (R + h)² = R² + d². Resuelve para h (haciendo la suposición de que R>>h y expresa el radio de la Tierra en millas, aproximadamente 3959) para conseguir la expresión:d = SQRT(2*R*h)

Anuncio

Consejos

Estos cálculos se utilizan con mayor frecuencia miras al horizonte verdadero, o hacia donde el cielo y la Tierra se reuniría si no hubieran todas esas barreras y obstáculos en su camino (que es el caso en el mar, a menos que haya una masa de tierra en el camino). En la Tierra, sin embargo, pueden haber montañas o edificios en frente del horizonte verdadero, en cuyo caso estos cálculos te ayudarán a determinar qué tan lejos está del verdadero horizonte, pero tendrás que virar sobre cualquier distancia adicional creada pasando por encima o rodeando los obstáculos que se encuentren en el camino.

Anuncio