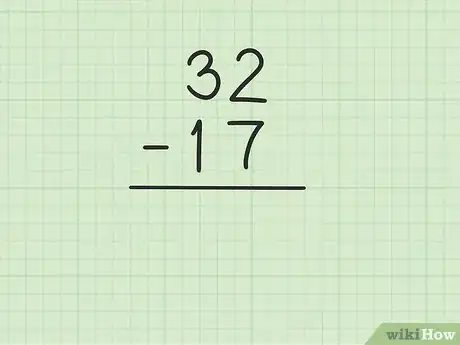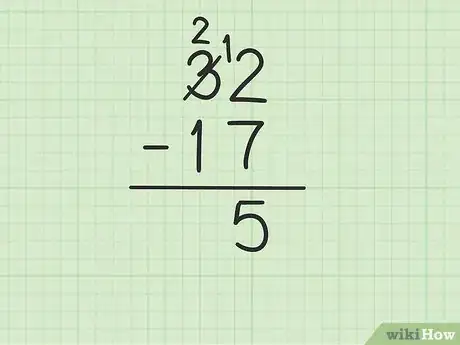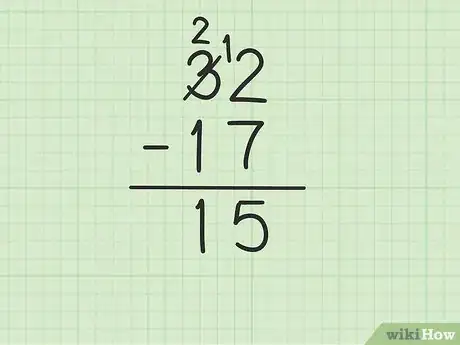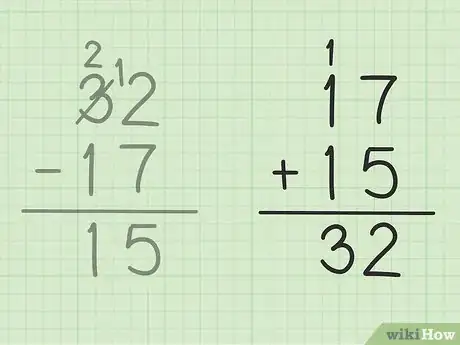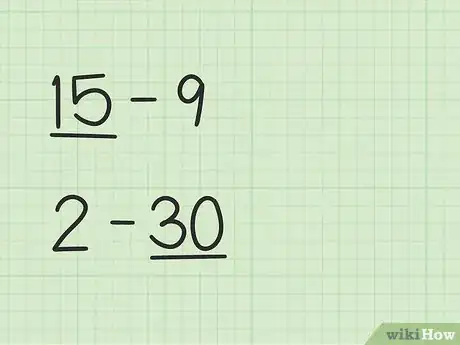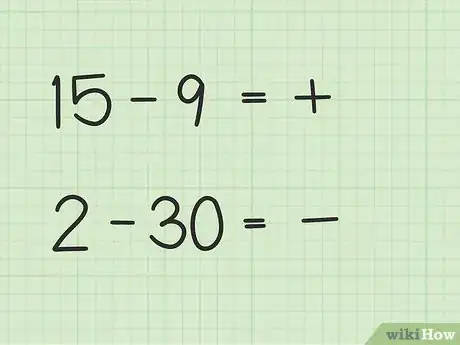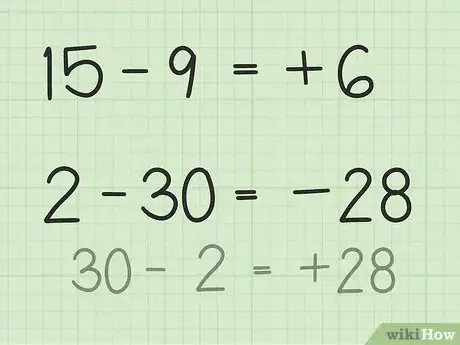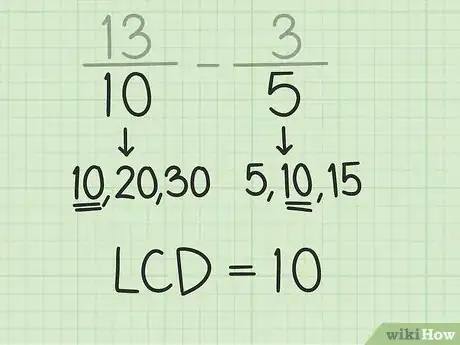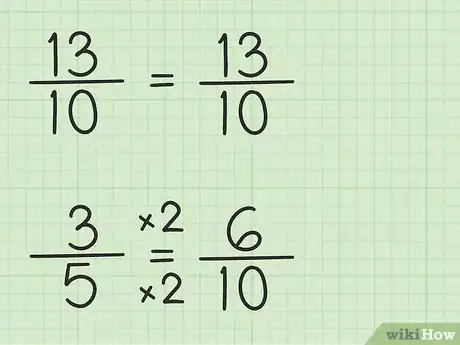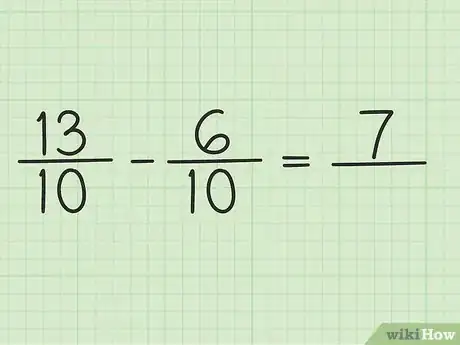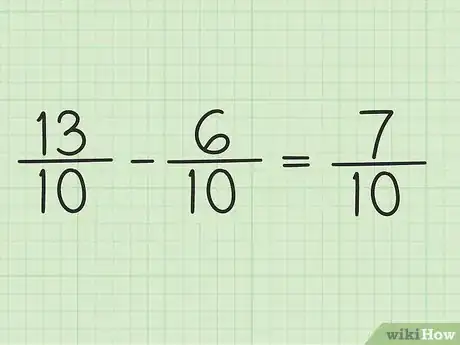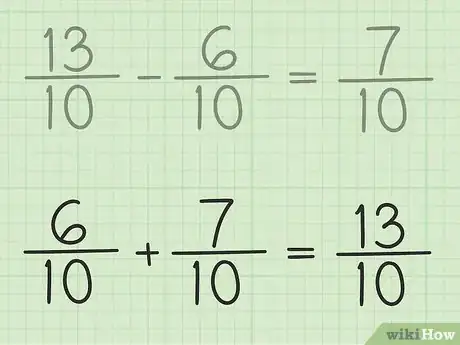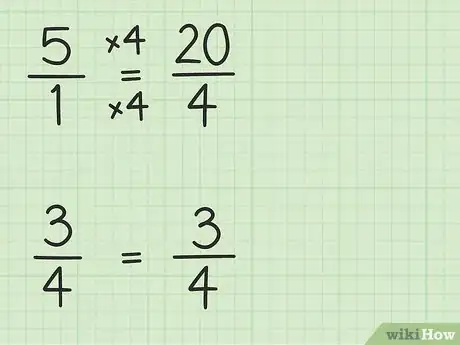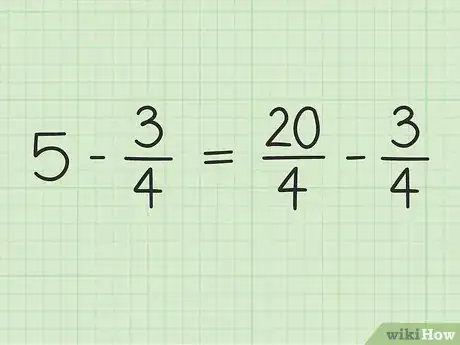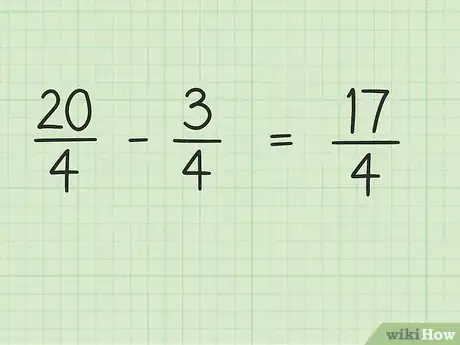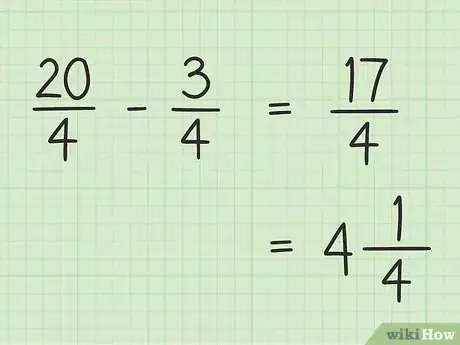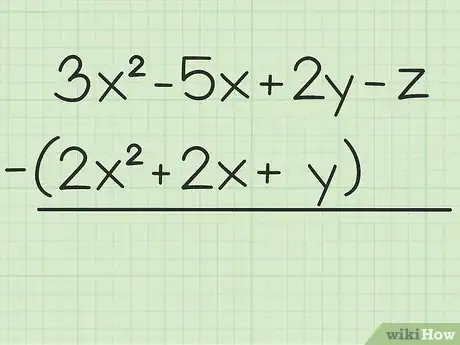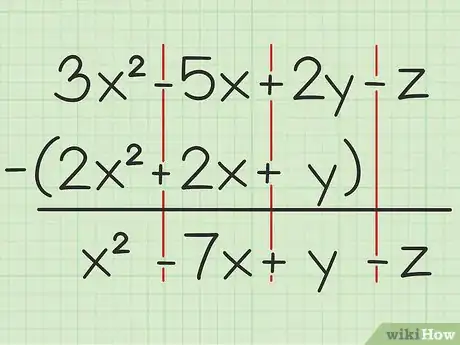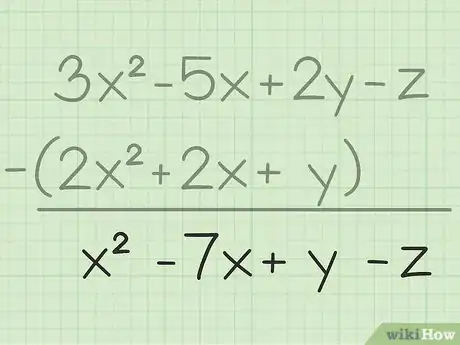wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 16 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 150 404 veces.
La resta consiste simplemente en quitarle un número a otro. Restar un número entero de otro es bastante sencillo, pero la resta puede ser un poco más complicada cuando trabajas con fracciones o decimales. Una vez que domines la resta, podrás pasar a conceptos matemáticos más difíciles y serás capaz de sumar, multiplicar y dividir números con gran facilidad.
Pasos
Método 1
Método 1 de 6:Restar números enteros grandes tomando prestado
-
1Escribe el número mayor. Supongamos que el problema es: 32 – 17. Primero escribe el 32.
-
2Escribe el número menor justo debajo del primero. Asegúrate de alinear las columnas de las decenas y de las unidades, de modo que el 3 en "32" se encuentre justo encima del 1 en "17" y que el 2 en "32" esté encima del "7" en 17.
-
3En la columna de las unidades, resta el número que se encuentra en la parte inferior del que está en la parte superior. Esto puede ser un poco complicado, ya que el número inferior es mayor que el superior. En este caso, 7 es mayor que 2. Esto es lo que necesitas hacer:
- Deberás "tomar prestado" del 3 en "32" (también conocido como reagrupación) con la finalidad de convertir ese 2 en 12.
- Tacha el 3 en "32" y conviértelo en 2, mientras que el 2 se vuelve 12.
- Ahora tienes 12 – 7, cuyo resultado es 5. Escribe un 5 debajo de los dos números que restaste, de modo que se alinee con la columna de las unidades formando una fila nueva.
-
4En la columna de las decenas, resta el número que se encuentra en la parte inferior del que está en la superior. Recuerda que el 3 ahora es un 2. A continuación, resta el 1 en 17 del 2 que está encima para obtener (2-1) 1. Escribe 1 debajo de los números en la columna de las decenas, a la izquierda del 5 que se encuentra en la columna de las unidades en la fila de la resta o diferencia. Debes haber escrito 15. Esto significa que 32 - 17 = 15.
-
5Revisa la operación. Si quieres asegurarte de haber restado correctamente ambos números, todo lo que tienes que hacer es sumar la respuesta al número menor para obtener como resultado el número mayor. En este caso, suma la respuesta (15) al número menor ubicado en el sustraendo (17). 15 + 17 = 32, eso significa que has restado correctamente. ¡Bien hecho!Anuncio
Método 2
Método 2 de 6:Restar números enteros pequeños
-
1Identifica el número mayor. Un problema como 15 – 9 necesitará una técnica de visualización distinta que un problema como 2 - 30.
- En el problema 15 - 9, el primer número (15) es mayor que el segundo (9).
- En el problema 2 - 30, el segundo número (30) es mayor que el primero (2).
-
2Decide si la respuesta será un número positivo o negativo. Si el primer número es mayor, la respuesta será positiva. Si el segundo número es mayor, la respuesta será negativa.
- En el primer problema (15 – 9) la respuesta será positiva porque el primer número es mayor que el segundo.
- En el segundo problema (2 – 30) la respuesta será negativa porque el segundo número es mayor que el primero.
-
3Encuentra la diferencia entre los dos números. Para restar dos números, deberás visualizar la diferencia entre ellos y contar los números que hay en medio.
- Para el problema 15 - 9, visualiza una pila de 15 fichas de póquer. Quita 9 y verás que quedan 6. Por lo tanto, 15 - 9 = 6. También puedes imaginar una recta numérica. Piensa en los números del 1 al 15 y luego quita o retrocede 9 unidades para obtener 6.
- Para el problema 2 - 30, lo más fácil que puedes hacer es invertir los números y luego efectuar la resta dándole un signo negativo a la respuesta. De modo que 30 - 2 = 28, dado que 28 es solo dos números menor que 30. A continuación, dale un signo negativo a la respuesta, puesto que al principio determinaste que sería negativa debido a que el segundo número es mayor que el primero. Por lo tanto, 2 - 30 = -28.
Anuncio
Método 3
Método 3 de 6:Restar decimales
-
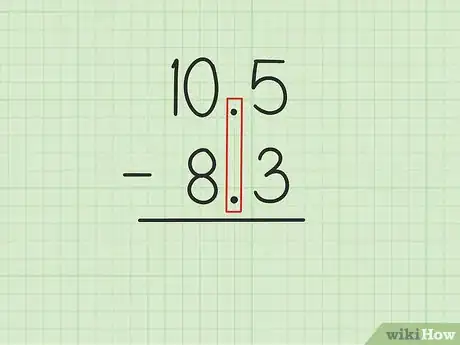
1Escribe el número mayor encima del menor con los decimales alineados. Supongamos que tienes el siguiente problema: 10,5 – 8,3. Escribe 10,5 encima de 8,3 de manera tal que las comas decimales de ambos números estén alineadas. El ,5 en 10,5 debe estar encima del ,3 en 8,3, mientras que el 0 en 10,5 debe estar encima del 8 en 8,3.
- Si tienes un problema en el que ambos números no tienen la misma cantidad de cifras después de la coma decimal, escribe un cero en los espacios vacíos hasta que estén igualados. Por ejemplo, si tienes el problema 5,32 – 4,2, puedes escribirlo como 5,32 = 4.20. Esto no cambiará el valor del segundo número pero sí hace que restar ambos números sea más sencillo.
-
2En la columna de los decimales, resta el número que se encuentra en la parte inferior del que está en la parte superior. Debes seguir el mismo procedimiento que harías al sustraer números enteros regulares, con la excepción de que no debes olvidarte de alinear los decimales de ambos números para conservar el decimal en la respuesta. En este caso, necesitas restar 3 de 5. 5 - 3 = 2, así que debes escribir un 2 debajo del 3 en 8,3.
- Asegúrate de colocar esa coma decimal en la respuesta. De momento, la respuesta debe estar así: ,2.
-
3En la columna de las unidades, resta el número que se encuentra en la parte inferior del que está en la parte superior. Ahora necesitarás restar 8 de 0. Toma prestado el 1 al lado del 0 para convertirlo en 10 y réstale 8 (10 - 8) para obtener 2. También puedes restar 8 de 10 sin tomar prestado nada ya que no hay ningún número en el sustraendo de la columna de las decenas. Escribe la respuesta debajo del 8, a la izquierda de la coma decimal.
-
4Indica la respuesta final. La respuesta final es 2,2.
-
5Revisa la operación. Si quieres asegurarte de haber restado los decimales correctamente, todo lo que tienes que hacer es sumar la respuesta al número menor para obtener como resultado el número mayor. 2,2 + 8,3 = 10,5, listo.Anuncio
Método 4
Método 4 de 6:Restar fracciones
-
1Alinea los denominadores y los numeradores de las fracciones. Supongamos que tienes el siguiente problema: 13/10 - 3/5. Escribe el problema de modo tal que ambos numeradores (13 y 3) y ambos denominadores (10 y 5) estén directamente uno frente al otro. Un signo de resta separará a ambos números. Esto te ayudará a visualizar el problema y a obtener una solución con mayor facilidad.
-
2Halla el mínimo común denominador. El mínimo común denominador es el menor número divisible por ambos números. En este ejemplo, necesitarás hallar el mínimo común denominador de los números 10 y 5. Puedes observar que 10 es el mínimo común denominador de ambos números, porque es divisible por 10 y por 5.
- Ten en cuenta que el mínimo común denominador de dos números no siempre es uno de ellos. Por ejemplo, el mínimo común denominador de 3 y 2 es 6, porque es el menor número divisible por ambos.
-
3Vuelve a escribir las fracciones con los mismos denominadores. La fracción 13/10 puede escribirse de la misma manera, ya que el denominador (10) se incluye en el mínimo común denominador (10) exactamente una vez. Sin embargo, la fracción 3/5 debe volverse a escribir porque el denominador (5) se incluye en el mínimo común denominador (10) dos veces. De modo que la fracción 3/5 debe multiplicarse por 2/2 para tener 10 en el denominador. Por lo tanto, 3/5 x 2/2 = 6/10. Has creado una fracción equivalente. 3/5 es igual a 6/10, aunque esta fracción te permite restar 6/10 de 13/10.
- El nuevo problema es: 13/10 - 6/10.
-
4Resta los numeradores de ambas fracciones. Simplemente resta 13 - 6 para obtener 7. No debes cambiar los denominadores de las fracciones.
-
5Escribe el nuevo numerador sobre el mismo denominador para obtener la respuesta final. El nuevo numerador es 7 y ambas fracciones tienen el denominador 10, por lo tanto, la respuesta final es 7/10.
-
6Revisa la operación. Si quieres asegurarte de haber restado los decimales correctamente, todo lo que tienes que hacer es sumar la respuesta al número menor para obtener como resultado el número mayor. Por lo tanto, 7/10 + 6/10 = 13/10. Listo.Anuncio
Método 5
Método 5 de 6:Restar una fracción de un número entero
-
1Escribe el problema. Supongamos que el problema es el siguiente: 5 - 3/4. Escríbelo.
-
2Convierte el número entero en una fracción con el mismo denominador que la fracción. Deberás convertir el 5 en una fracción que tenga un denominador de 4 con la finalidad de restar ambos números. Primero puedes considerar a 5 como una fracción (5/1). Luego, puedes multiplicar tanto el número superior como el inferior de la nueva fracción por 4 para crear dos fracciones con el mismo denominador. Por lo tanto, 5/1 x 4/4 = 20/4. Esta fracción es igual a 5, pero te permite restar ambas fracciones.
-
3Vuelve a escribir el problema. Puedes volver a escribir el nuevo problema de la siguiente manera: 20/4 - 3/4.
-
4Resta los numeradores de las fracciones y mantén el mismo denominador. A continuación, simplemente resta 3 de 20 para obtener la respuesta final. 20 - 3 = 17, de modo que 17 es el nuevo numerador. Puedes dejar el denominador tal cual.
-
5Escribe la respuesta final. La respuesta final es 17/4. Si quieres formularla como un número mixto, simplemente divide el 17 entre 4 para obtener 4, con un residuo de 1. Esto hará que tu respuesta final (17/4) sea igual a 4 1/4.Anuncio
Método 6
Método 6 de 6:Restar variables
-
1Escribe el problema. Supongamos que el problema es el siguiente: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Escribe el primer conjunto de términos encima del segundo.
-
2Resta los términos semejantes. Cuando trabajas con variables, solo puedes sumar o restar términos que tengan la misma variable y que estén escritos en el mismo grado. Por ejemplo, puedes restar 4x2 de 7x2, pero no 4x de 4y. Esto significa que puedes descomponer el problema de esta manera:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
-
3Indica tu respuesta final. Ahora que has restado todos los términos semejantes posibles, todo lo que puedes hacer es indicar la respuesta final, la cual contendrá cada uno de los términos que restaste. Esta es la respuesta final:
- 3x2 - 5x + 2y - z - (2x2 + 2x + y) = x2 - 7x + y - z
Anuncio
Consejos
- Descompón números grandes en partes más pequeñas. Por ejemplo: 63 - 25. Nada te exige que debas retirar 25 fichas de una sola vez. Podrías quitar 3 para tener 60; quitar otras 20 para tener 40; luego quita las últimas 2. Resultado: 38. No necesitaste tomar prestado.
Advertencias
- Si tienes una mezcla de números positivos y negativos, las cosas pueden tornarse mucho más complicadas. Consulta el artículo de wikiHow llamado Cómo sumar y restar números enteros
Acerca de este wikiHow
Para restar números enteros considerables, primero tendrás que anotar el número más grande y colocar el más pequeño directamente debajo de él. Luego tendrás que restar el número de la parte inferior al de la parte superior en la columna de unidades, y hacer lo mismo en la columna de decenas, ¡así obtendrás la respuesta final!