Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 195 610 veces.
La media geométrica es otra alternativa para encontrar el valor promedio de un conjunto de números, solo que en vez de sumar los valores y dividirlos como normalmente se harías para calcular la media aritmética, primero tienes que multiplicarlos y luego calcular la raíz. La media geométrica se puede usar para calcular tasas de retorno en finanzas o mostrar cuánto ha crecido algo a lo largo de un período específico. Para poder encontrar la media geométrica, multiplica todos los valores y posteriormente calcula la raíz n-ésima siendo n igual a la cantidad total de valores del conjunto. Si quieres, también puedes calcular la media geométrica a través de las funciones logarítmicas de la calculadora.
Pasos
Método 1
Método 1 de 2:Encontrar la media geométrica de un conjunto de valores
-
1Multiplica los valores para los cuales quieras encontrar la media geométrica. Para encontrar el producto puedes usar una calculadora o hacer los cálculos a mano. Multiplica todos los números del conjunto de datos que vas a calcular para hallar el producto. Anota el producto para no olvidarlo.[1]
- Por ejemplo, si el conjunto de valores es 3, 5 y 12, entonces deberás escribir: (3 x 5 x 12) = 180.
- Otro ejemplo: si quieres calcular la media geométrica para un conjunto de datos que tiene los números 2 y 18, entonces escribe (2 x 18) = 36.
-
2Calcula la raíz n-ésima del producto siendo n la cantidad de valores. Cuenta cuántos valores tiene el conjunto de datos cuya media geométrica vas a calcular y así obtendrás el valor de n. Ese valor determinará el grado de la raíz que debes aplicarle al producto. Por ejemplo, si son dos valores, deberás calcular la raíz cuadrada; si son tres, la raíz cúbica y así sucesivamente. Utiliza la calculadora para resolver la ecuación y anota la respuesta.[2]
- Por ejemplo, para el conjunto de datos 3, 5 y 12, escribe: ∛(180) ≈ 5,65.
- En el segundo ejemplo de 2 y 12, escribe: √(36) = 6.
Variación: también puedes escribir el valor como exponente 1/n si es más fácil ingresarlo así en la calculadora. Por ejemplo, para el conjunto 3, 5 y 12 puedes escribir (180)1/3 en vez de ∛(180).
-
3Convierte los porcentajes a sus respectivos multiplicadores decimales. Si el conjunto de números se expresa en forma de aumento o disminución porcentual, evita usar ese valor porcentual para la media geométrica, ya que podrías sesgar los resultados. Si el porcentaje es un aumento, mueve la coma decimal 2 lugares hacia la izquierda y súmale 1. Si el porcentaje es una disminución, mueve la coma decimal 2 lugares hacia la izquierda y réstasela a 1.[3]
- Por ejemplo, imagina que quieres encontrar la media geométrica del valor de un objeto que aumenta 10 % y luego disminuye 3 %.
- Convierte 10 % a decimal y súmale 1. Obtendrás 1,10.
- Luego convierte el 3 % a decimal y réstaselo a 1. Obtendrás 0,97.
- Utiliza los dos valores decimales para hallar la media geométrica: √(1,10 x 0,97) ≈ 1,03.
- Convierte el número nuevamente a porcentaje moviendo la coma decimal 2 lugares a la derecha y restándole 1. Obtendrás un valor de aumento del 3 %.
Anuncio
Método 2
Método 2 de 2:Calcular la media geométrica con logaritmos
-
1Suma los valores logarítmicos de todos los números del conjunto. La función LOG calcula el valor tomando como base 10 y determina cuántas veces tienes que multiplicar 10 para llegar a ese valor. Ubica la función LOG en tu calculadora (generalmente está en el lado izquierdo del teclado), presiona ese botón e ingresa el primer valor del conjunto. Escribe un signo "+" antes de presionar LOG para el segundo valor. Sigue separando las funciones LOG de cada valor con signos más antes de calcular la suma.[4]
- Por ejemplo, para el conjunto 7, 9 y 12, deberás escribir log(7) + log(9) + log(12) antes de presionar "=" en la calculadora. Al resolver las funciones, la suma será aproximadamente 2,878521796.
- También puedes calcular cada uno de los logaritmos en forma separada y sumar las respuestas.
-
2Divide la suma de los valores logarítmicos entre la cantidad de valores del conjunto. Cuenta la cantidad de valores del conjunto y luego divide entre ese número la suma que acabas de calcular. La respuesta será el valor logarítmico de la media geométrica.[5]
- En este ejemplo tu conjunto tiene 3 números, por lo tanto, deberás calcular 2,878521796 / 3 ≈ 0,959507265.
-
3Calcula el antilogaritmo del cociente para determinar la media geométrica. La función antilogaritmo es la inversa a la función LOG en la calculadora. Lo que hace es regresar el valor nuevamente a la base 10. Busca el símbolo "10x" en la calculadora (generalmente es la función secundaria del botón LOG), presiona el botón "2nd" en la esquina superior izquierda de la calculadora seguido del botón LOG para activar el antilogaritmo. Escribe el cociente que has obtenido en el paso anterior para resolver la ecuación.[6]
- Para este ejemplo, la calculadora mostrará: 10(0,959507265) ≈ 9,11.
Anuncio
Consejos
Cosas que necesitarás
- calculadora
Referencias
- ↑ https://www.mathsisfun.com/numbers/geometric-mean.html
- ↑ https://www.mathsisfun.com/numbers/geometric-mean.html
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
- ↑ https://www.statisticshowto.datasciencecentral.com/geometric-mean-2/
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
- ↑ https://www.statisticshowto.datasciencecentral.com/geometric-mean-2/#GMCL




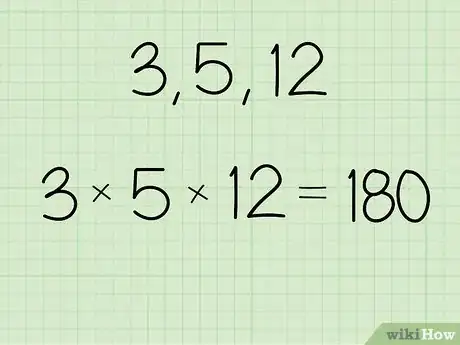
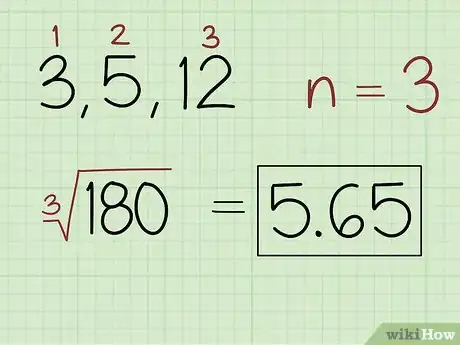
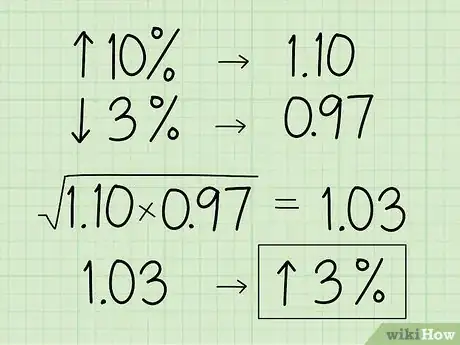

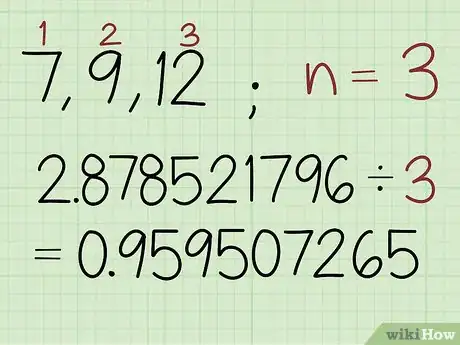








-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)





wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 195 610 veces.