wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 13 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 62 231 veces.
Debido a que hay tantos sistemas de medición diferentes en el mundo, la conversión de unidades puede ser útil. Para ello, deberás comprender las fracciones (a menos que vayas a trabajar dentro del sistema métrico). Independientemente del sistema que uses, siempre debes escribir con cuidado las unidades en cada paso para poder saber en dónde estás.
Pasos
Método 1
Método 1 de 3:Convertir unidades
-
1Compara ambas unidades. Ambas deben medir lo mismo. Por ejemplo, en el problema "convierte 2 pulgadas a centímetros", tanto las pulgadas como los centímetros miden la longitud. No podrás convertir entre dos unidades si estas miden dos cosas distintas (por ejemplo, la longitud y el peso).
- Con frecuencia, el área, la longitud y el volumen ocasionan confusión. Estas miden tres cosas diferentes. Debes recordar que las unidades "cuadradas" o "2" se refieren al área, mientras que la unidades "cúbicas" o "3" se refieren al volumen.
- Este ejemplo también puede escribirse como 2 in = ? cm.
-
2Busca la conversión. Debes saber en qué proporción una unidad es más grande que la otra antes de poder realizar el cálculo. En caso de que encuentres una conversión con muchas cifras decimales, debes redondear a la cifra significativa más cercana. Si no sabes qué es una cifra significativa, debes redondear el número al segundo o tercer dígito.
- Por ejemplo, para convertir 2 pulgadas a centímetros, es necesario saber que 1 pulgada = 2,54 cm.
-
3Escribe la conversión en la forma de una fracción. Escríbela como una fracción, incluyendo las unidades. La unidad con la que empieces debe quedar en la parte inferior (es decir, el denominador) y la unidad de destino debe quedar en la parte superior (es decir, el numerador).[1]
- Por ejemplo, escribe 2,54 cm/1 in. Esto puede leerse como "2,54 cm por pulgada".
-
4Escribe un problema de multiplicación empleando el número original y la fracción. Obtendrás la respuesta al multiplicar ambos números. Para empezar, debes anotar el problema de multiplicación, incluyendo las unidades después de cada valor.
- 2 in x 2,54 cm/1 in = ?
-
5Resuelve el problema de multiplicación. Debes monitorear las unidades al realizar este cálculo. Todas las unidades en la ecuación deben estar presentes en cada paso.
- 2 in x 2,54 cm/1 in
- = (2 in x 2,54 cm)/1 in
- = (5,08 in x cm)/ in
-
6Cancela las unidades que estén en la parte superior e inferior. En caso de que haya unidades que estén tanto en la parte superior como en la inferior de la fracción, debes tacharlas. La respuesta serán las unidades con las que te quedes.
-
(5,08
inx cm)/in - = 5,08 cm
-
(5,08
-
7Corrige los errores. En caso de que no puedas cancelar las unidades, debes intentarlo de nuevo. Es posible que hayas colocado la mitad incorrecta de la fracción en la parte superior.
- Por ejemplo, al multiplicar 2 pulgadas x (1 in / 2,54 cm), las unidades de la respuesta serán "in x in / cm", lo cual no tiene sentido. Debes darte cuenta de que, para cancelar las pulgadas, debes invertir la fracción e intentarlo de nuevo con la operación 2 pulgadas x (2,54 cm / 1 in).
Anuncio
Método 2
Método 2 de 3:Convertir valores con múltiples unidades
-
1Anota el problema. Determina qué es exactamente lo que te pide el problema y escríbelo como si fuera un problema de matemáticas. Este es un ejemplo:
- Si una bicicleta se desplaza a 10 millas por hora, ¿cuántos pies se desplaza en un minuto?
- Debes escribir esto como "10 millas / hora = ? pies / minuto" o "10 millas / h = ? pies / min".
-
2Determina la conversión para una unidad. Ten en cuenta que solo se puede hacer conversiones entre dos unidades que midan lo mismo. En el ejemplo, hay unidades que miden longitud (millas y pies) y también tiempo (horas y minutos). Debes empezar con uno de estos pares y encontrar la conversión entre ellos.
- Por ejemplo, 1 milla = 5280 pies.
-
3Multiplica el número por la fracción de conversión. De la misma forma como se describió en la sección anterior, se puede escribir la conversión como una fracción para así cancelar las unidades. Ten cuidado de que todas las unidades estén incluidas en el cálculo.
- 10 millas / h) x 5280 pies / milla
- = 52 800 millas x pies / h x millas
-
4Cancela las unidades. Una de ellas debe estar tanto en la parte superior como en la inferior de manera que puedas cancelarla. Aún no has terminado, pero ya estás cerca del final.
- 52 800
millasx pies / h xmillas - = 52 800 pies / h
- 52 800
-
5Multiplica de la misma forma por otra fracción de conversión. Elige una unidad que no hayas convertido y escribe la conversión en la forma de una fracción. Recuerda que debes disponerla de manera que las unidades puedan cancelarse al multiplicar.
- Siguiendo con el ejemplo, aún falta convertir las horas a minutos. 1 hora = 60 minutos.
- Por el momento, lo que tenemos es 52 800 pies / h. Debido a que las horas (h) se encuentran en la parte inferior, estas deben estar en la parte superior en la nueva fracción: 1 hora / 60 minutos.
- 52 800 pies / h x 1 h / 60 min
- = 880 pies x h / h x min
-
6Cancela las unidades. Como ocurrió antes, debería cancelarse otra unidad.
- 880 pies x
h/hx min - = 880 pies / min
- 880 pies x
-
7Repite el procedimiento hasta terminar la conversión. Si obtienes la respuesta en las unidades a las que querías realizar la conversión, habrás terminado con el problema. Si esto aún no sucede, convierte otras unidades siguiendo el mismo método.
- Cuando te acostumbres a este método, podrás escribir todas las conversiones en la misma línea.[2] El problema del ejemplo podría resolverse así:
- 10 millas/h x 5280 pies/milla x 1 h/60 min
- =10
millas/hx 5280 pies/millax 1h/60 min - = 10 x 5280 pies x 1/60 min
- = 880 pies / min
Anuncio
Método 3
Método 3 de 3:Convertir dentro del sistema métrico
-
1Comprende el sistema métrico. Este sistema, también conocido como el sistema decimal, se diseñó para facilitar la conversión. Para poder convertir de una unidad métrica a otra, solo debes trabajar con números redondos, como 10, 100, 1000, etc.
-
2Aprende los prefijos. Las unidades de medición en el sistema métrico emplean prefijos. De esta forma, se puede ver cuán grande o pequeña es la medida. El siguiente es un ejemplo empleando las unidades para el peso, aunque los mismos prefijos aplican para todas las demás unidades métricas.[3] Los prefijos que figuran a continuación se encuentran en cursiva, aunque también es posible realizar la mayor parte de las conversiones solo con los prefijos más comunes, los que se encuentran en negrita.
- kilogramo = 1000 gramos
- hectogramo = 100 gramos
- decagramo = 10 gramos
- gramo = 1 gramo
- decigramo = 0,1 gramos (una décima)
- centigramo = 0,01 gramos (una centésima)
- miligramo = 0,001 gramos (una milésima)
-
3Emplea los prefijos en la conversión. No tendrás que buscar cuál es la conversión cada vez que tengas que realizarla si sabes cuáles son los prefijos. Estos de por sí te brinda información sobre la conversión. A continuación figuran algunos ejemplos:
- Para la conversión de kilómetros a metros: "kilo" quiere decir 1000, por lo que 1 km = 1000 metros.
- Para la conversión de gramos a miligramos: "mili" quiere decir 0,001, por lo que 1 miligramo = 0,001 gramos.
-
4Mueve el punto decimal en lugar de realizar cálculos. Lo mejor de la conversión dentro del sistema métrico es que no es necesario realizar cálculos. La multiplicación de un número por 10 equivale a mover el punto decimal a la derecha. La división de un número entre 10 equivale a mover el punto decimal a la izquierda. Este es un ejemplo de cómo emplear este método:
- Problema: convertir 65,24 kilogramos a gramos.
- 1 kilogramo = 1000 gramos. Cuenta la cantidad de ceros. Estos son tres, lo que quiere decir que debes multiplicar tres veces por 10 o simplemente mover el punto decimal tres espacios hacia la derecha.
- 65,24 x 10 = 652,4 (una multiplicación)
- 652,4 x 10 = 6524 (dos multiplicaciones)
- 6524 x 10 = 65 240 (tres multiplicaciones)
- Respuesta: 65 240 gramos.
-
5Practica los problemas más difíciles. Cuando ambas unidades entre las cuales quieras convertir tienen prefijos, esto se torna un poco más complicado. Para resolverlo, lo más fácil es convertir primero a la unidad base (la que no tenga un prefijo) y luego convertir a la unidad final. Este es un ejemplo:
- Problema: convertir 793 mililitros a decalitros.
- 1 mililitro = 0,001 litros. Como hay tres ceros, se debe mover el punto decimal tres espacios hacia la izquierda (no olvides que debes moverlo hacia la izquierda para dividir).
- 793 mililitros = 0,793 litros
- 10 litros = 1 decalitro, por lo que 1 litro = 0,1 decalitros. Como solo hay un cero, el punto decimal se mueve un espacio hacia la izquierda.
- 0,793 litros = 0,0793 decalitros.
-
6Revisa la respuesta. El error que más fácilmente se comete es multiplicar en lugar de dividir o viceversa. Por tanto, al obtener la respuesta final, debes revisar que esta tenga sentido:
- Si la conversión fue a una unidad más grande, el número debe ser más pequeño (por ejemplo, 10 milímetros se convierten en 1 centímetro).
- Si la conversión fue a una unidad más pequeña, el número debe ser más grande (por ejemplo, 1 centímetro se convierte en 10 milímetros).
- En caso de que obtengas un resultado que no concuerde con esto, debes revisar lo que hayas hecho.
Anuncio
Consejos
- Puede ser difícil convertir las recetas, ya que, en algunos países, los ingredientes sólidos se miden por peso (en gramos), mientras que, en otros, se miden por volumen (cucharaditas, tazas). Puedes buscar en línea una calculadora que realice las conversiones para ese ingrediente en particular mediante su densidad.
Referencias
Acerca de este wikiHow
1. Verifica que las dos unidades que vayas a convertir se usen para medir dimensiones semejantes, por ejemplo, longitud o ancho. 2. Busca el factor de conversión para esas unidades. 3. Escribe la conversión en forma de fracción, poniendo en la parte inferior la unidad con la que empieces y en la parte superior la unidad de destino. 4. Multiplica el número original por la fracción, manteniendo todas las unidades (por ejemplo, pulgadas o metros) en su lugar en cada paso del problema. 5. Cancela las unidades que estén tanto en la parte superior como inferior de la fracción. 6. El número y la unidad restantes serán el resultado de la conversión.




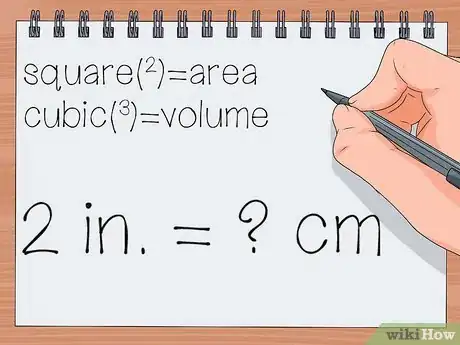
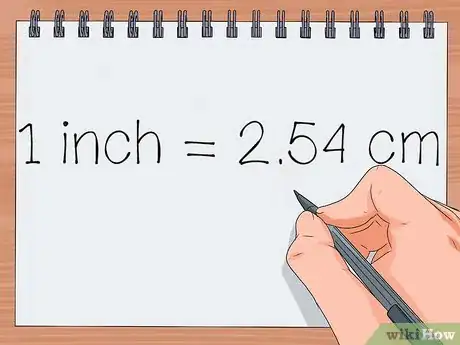

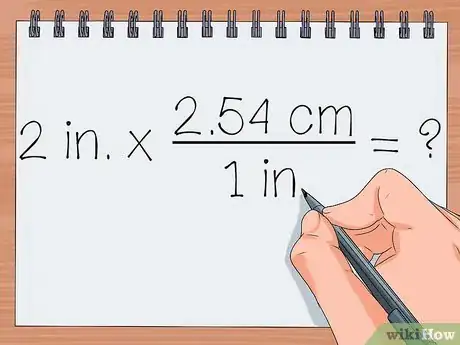

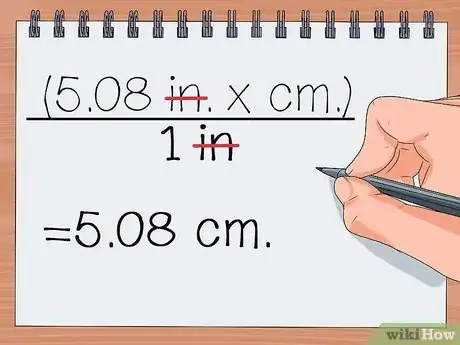

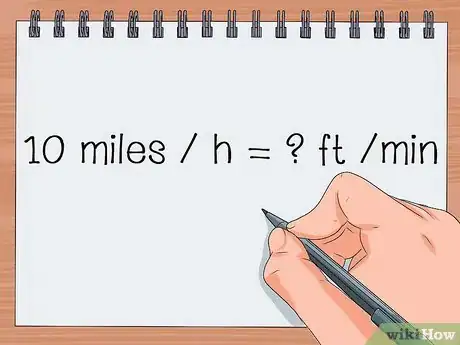

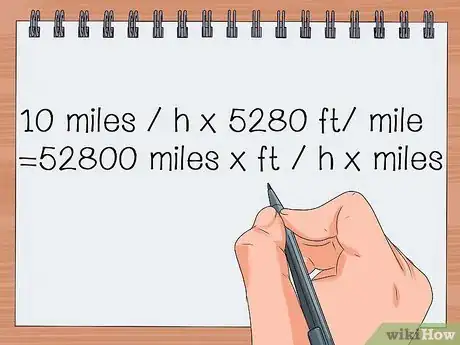
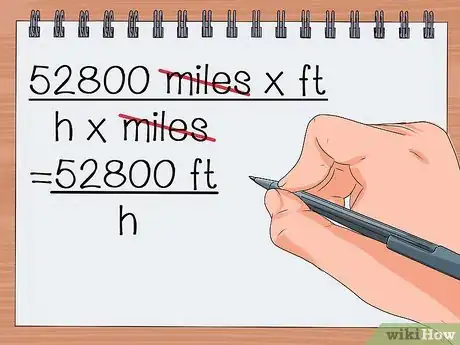
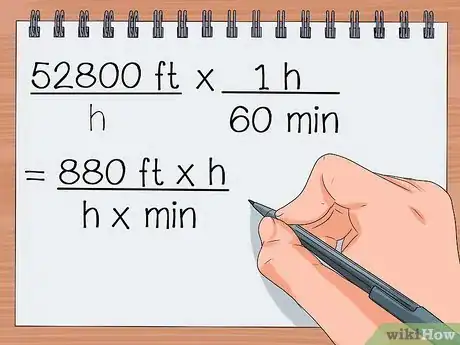
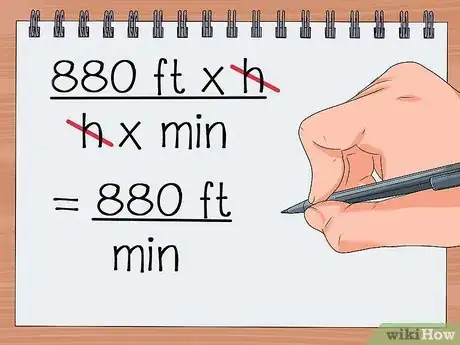














-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)




