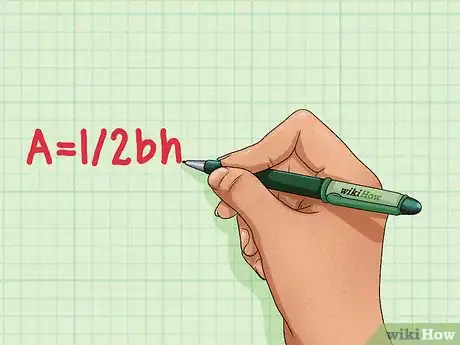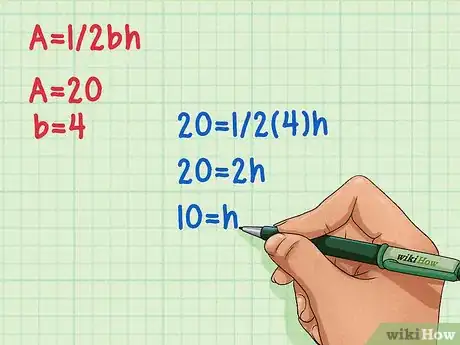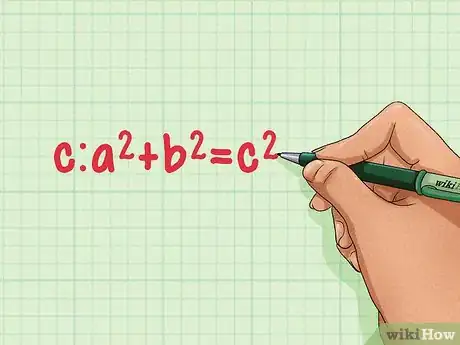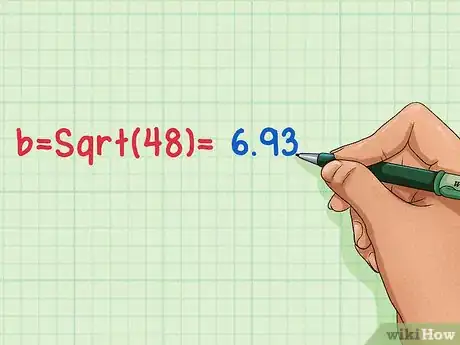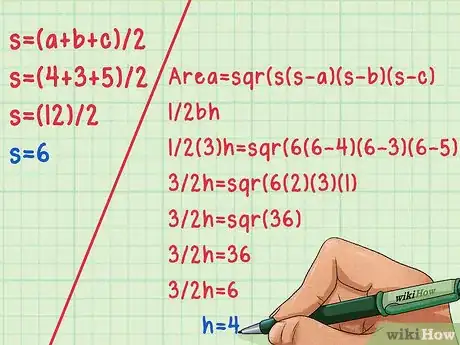Cómo encontrar la altura de un triángulo

Información del autor

Para calcular el área de un triángulo debes conocer su altura. Si no tienes esta información, puedes calcularla fácilmente tomando como base lo que sabes. Este artículo te enseñará dos maneras de encontrar la altura de un triángulo usando la información que tienes.

Método 1

Método 1 de 3:
Usar la base y el área para hallar la altura

1
Recuerda la fórmula para el área de un triángulo. La fórmula para el área de un triángulo es A=1/2bh.^{[1]
X
Fuente de investigación}
- A = área del triángulo
- b = longitud de la base del triángulo
- h = altura de la base del triángulo
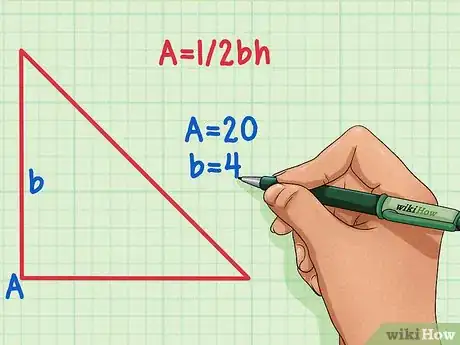
2
Mira el triángulo y determina qué variables conoces. En este caso, ya conoces el área, así que asigna ese valor a A. También debes conocer el valor de la longitud de un lado, así que asigna ese valor a b. Si no conoces el área ni la longitud de un lado, tendrás que intentar con otro método.
- Cualquier lado de un triángulo puede ser la base, sin importar cómo esté dibujado el triángulo. Para visualizarlo, solo imagina que rotas el triángulo hasta que la longitud del lado conocida esté en la parte inferior.
- Por ejemplo, si conoces que el área de un triángulo es 20 y un lado es 4, entonces: A = 20 y b = 4.
3
Inserta los valores a la ecuación A=1/2bh y haz la operación. Primero multiplica la base (b) por ½, luego divide el área (A) por el producto. El valor que resulta será la altura del triángulo.
- En el ejemplo: 20 = 1/2(4)h
- 20 = 2h
- 10 = h

Método 2

Método 2 de 3:
Hallar la altura de un triángulo equilátero

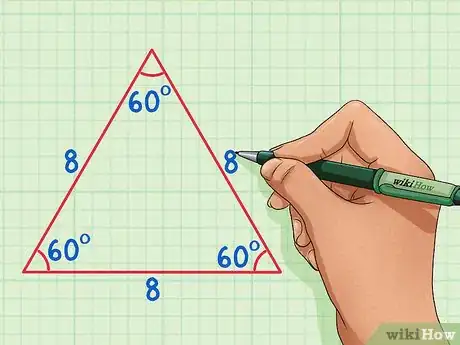
1
Recuerda las propiedades del triángulo equilátero. Un triángulo equilátero tiene tres lados y tres ángulos iguales (el valor de cada uno es de 60 grados). Si cortas a la mitad un triángulo equilátero, te quedarán dos triángulos rectángulos congruentes.^{[2]
X
Fuente de investigación}
- En este ejemplo, se usará un triángulo equilátero con lados de longitud 8.
2
Recuerda el teorema de Pitágoras. El teorema de Pitágoras establece que para cualquier triángulo rectángulo con lados de longitud a y b y la hipotenusa de longitud c: a² + b² = c². Se puede usar este teorema para hallar la altura del triángulo equilátero.^{[3]
X
Fuente de investigación}
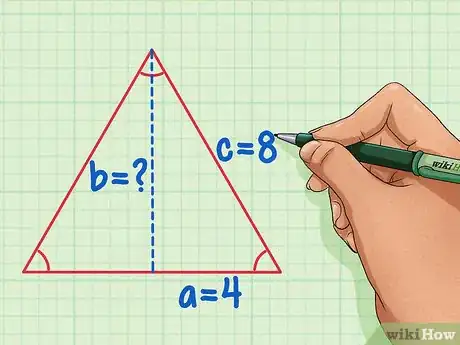
3
Divide a la mitad el triángulo equilátero y asigna valores a las variables a, b y c. La hipotenusa c será igual a la longitud original del lado. El lado a será igual a ½ de la longitud del lado y el lado b es la altura del triángulo que deseas hallar.
- Usando el ejemplo del triángulo equilátero con lados de 8: c = 8 y a = 4.
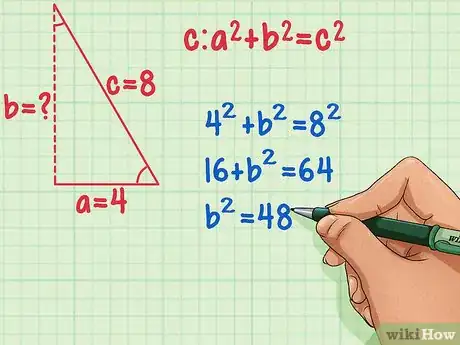
4
Inserta los valores al teorema de Pitágoras y resuelve b². Primero halla el cuadrado de c y a multiplicando cada número por sí mismo. Luego resta a² de c².
- 4² + b² = 8²
- 16 + b² = 64
- b² = 48
5
Halla la raíz cuadrada de b² para obtener la altura del triángulo. Usa la función de la raíz cuadrada en tu calculadora para hallar Sqrt(b²). La respuesta es la altura del triángulo equilátero.
- b = Sqrt (48) = 6.93

Método 3

Método 3 de 3:
Determinar la altura con los ángulos y los lados

1
Determina qué variables conoces. La altura de un triángulo se puede hallar si tienes un ángulo y un lado, si el ángulo está entre la base y el lado que tienes o si tienes los tres lados. Imagina que los lados del triángulo son a, b y c y los ángulos A, B y C.
- Si tienes los tres lados, puedes usar la fórmula de Herón y la fórmula para el área de un triángulo.
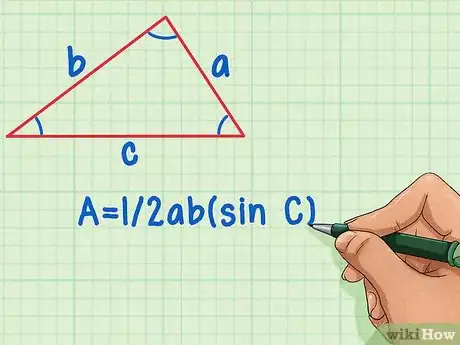
- Si tienes dos lados y un ángulo, puedes usar la fórmula para el área dados dos ángulos y un lado. A = 1/2ab(sin C).^{[4]
  X
  Fuente de investigación}
2
Usa la fórmula de Herón si tienes los tres lados. La fórmula de Herón tiene dos partes. Primero, debes hallar la variable s, que es igual a la mitad del perímetro del triángulo. Esto se hace con esta fórmula: s = (a+b+c)/2.^{[5]
X
Fuente de investigación}
- De manera que para un triángulo con lados a = 4, b = 3 y c = 5, s = (4+3+5)/2. Que es s = (12)/2. Que es s = 6.
- Luego puedes aplicar la segunda parte de la fórmula de Herón, área = sqr(s(s-a)(s-b)(s-c). Sustituye el área en la ecuación con su equivalente en la fórmula del área: 1/2bh (o 1/2ah o 1/2ch).
- Haz la operación para hallar h. Para el ejemplo del triángulo esto se debe ver como 1/2(3)h = sqr(6(6-4)(6-3)(6-5). Que es 3/2h = sqr(6(2)(3)(1). Que es 3/2h = sqr(36). Usa una calculadora para calcular la raíz cuadrada, que en este caso es 3/2h = 6. Por tanto, la altura es igual a 4, usando el lado b como la base.
3
Usa la fórmula del área dados dos lados y un ángulo si tienes un lado y un ángulo. Sustituye el área en la fórmula con su equivalente en el área de una fórmula de triángulo: 1/2bh. Esto te da una fórmula que se ve de esta manera: 1/2bh = 1/2ab(sin C). Lo cual se puede simplificar a h = a(sin C), eliminando de este modo una de las variables de lado.^{[6]
X
Fuente de investigación}
- Resuelve la ecuación con las variables dadas. Por ejemplo, con a = 3 y C = 40 grados, la ecuación se ve de esta manera: h = 3(sin 40). Usa una calculadora para terminar la ecuación, la que en el ejemplo da como resultado que el valor de h es aproximadamente 1,928.