Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 168 691 veces.
La división es una de las 4 operaciones principales de la aritmética junto con la suma, la resta y la multiplicación. Además de dividir números enteros puedes dividir decimales, fracciones o exponentes. Si uno de los números tiene un solo dígito, puedes usar la división corta. Si tiene más, deberás usar la división larga. De cualquier forma, es mejor que primero domines la división larga, ya que es la clave de toda la operación.
Pasos
Método 1
Método 1 de 5:División larga
-
1Escribe el problema utilizando la barra de división larga. Esta barra de división ( 厂 ) parece un paréntesis de cierre unido a una línea horizontal que se extiende por encima de la cadena de números que van debajo de la barra. Coloca el divisor, que es el número entre el cual dividirás, fuera de la barra de división; y el dividendo, que es el número a dividir, dentro de la barra de división larga.
- Problema de ejemplo 1 (para principiantes): 65 ÷ 5. Coloca el 5 afuera de la barra de división larga y el 65 dentro de ella. Debe quedar así 5厂65, pero con el 65 debajo de la línea horizontal.
- Problema de ejemplo 2 (intermedio): 136 ÷ 3. Coloca el 3 afuera de la barra de división larga y el 136 dentro de ella. Debe quedar así 3厂136, pero con el 136 debajo de la línea horizontal.
-
2Divide el primer dígito del dividendo entre el divisor. En otras palabras, determina cuántas veces cabe el divisor (el número que está fuera de la barra) en el primer dígito del dividendo. Coloca el número entero que obtengas como resultado arriba de la línea de la división, justo arriba del primer dígito del divisor.[1]
- En el problema de ejemplo 1 (5厂65), 5 es el divisor y 6 el primer dígito del dividendo (65). 5 cabe una sola vez en 6, por lo que arriba de la barra de división deberás colocar un 1 alineado verticalmente con el 6.
- En el problema de ejemplo 2 (3厂136), 3 (el divisor) no cabe en 1 (el primer dígito del dividendo) y no resulta en un número entero. Por lo tanto, escribe un 0 arriba de la barra de división alineado verticalmente con el 1.
-
3Multiplica el dígito que está arriba de la barra de división por el divisor. Toma el número que acabas de escribir arriba de la barra de división y multiplícalo por el divisor (el número que está a la izquierda de la barra de división). Escribe el resultado en una nueva fila debajo del dividendo, alineado con el primer dígito del dividendo.[2]
- En el problema de ejemplo 1 (5厂65), multiplica el número que está arriba de la barra (1) por el divisor (5), lo cual resulta en 1 x 5 = 5 y coloca la respuesta (5) justo debajo del 6 en 65.
- En el problema de ejemplo 2 (3厂136), hay un 0 arriba de la barra de división, así que cuando vayas a multiplicarlo por 3 (el divisor), el resultado será 0. Escribe un 0 en una nueva línea justo debajo de 136.
-
4Réstale el resultado de la multiplicación al primer dígito del dividendo. En otras palabras, réstale el número que acabas de escribir en la nueva fila debajo del dividendo al dígito del dividendo que está justo arriba de este. Escribe el resultado en una nueva fila, alineado con los dígitos del problema de sustracción.[3]
- En el problema de ejemplo 1 (5厂65), réstale 5 (el resultado de la multiplicación en la nueva fila) al 6 que está justo arriba de este (el primer dígito del dividendo): 6 – 5 = 1. Coloca el resultado (1) en una nueva fila, justo debajo del 5.
- En el problema de ejemplo 2 (3厂136), réstale 0 (el resultado de la multiplicación en la nueva fila) al 1 que está justo arriba de este (el primer dígito del dividendo). Coloca el resultado (1) en una nueva fila, justo debajo del 0.
-
5Arrastra el segundo dígito del dividendo hacia abajo. Baja el segundo dígito del dividendo a la nueva fila inferior, justo a la derecha del resultado de la resta que acabas de obtener.[4]
- En el problema de ejemplo 1 (5厂65), arrastra el 5 del 65 hacia abajo de modo que quede al lado del 1 que habías obtenido al restarle 5 a 6. Esto te dará 15 en esta fila.
- En el problema de ejemplo 2 (3厂136), arrastra el 3 del 136 y colócalo junto al 1 para formar el número 13.
-
6Repite el proceso de división larga (problema de ejemplo 1). Ahora usa el dividendo (el número que está a la izquierda de la barra de división) y el nuevo número que está en la fila inferior (formado por el resultado de la primera ronda de cálculos y el dígito que habías arrastrado). Tal como has hecho anteriormente, divide, multiplica y finalmente resta para obtener el resultado.[5]
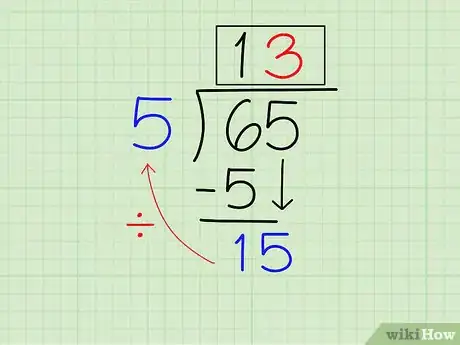
- Para continuar con 5厂65, divide 15 (el dividendo del nuevo número) entre 5 y escribe el resultado (3, ya que 15 ÷ 5 = 3) a la derecha del 1 que está arriba de la barra de división. Luego multiplica el 3 que está arriba de la barra de división por 5 (el dividendo) y escribe el resultado (15, ya que 3 x 5 = 15) debajo del 15 que está debajo de la barra de división. Por último, calcula 15 menos 15 y escribe 0 en la nueva fila inferior.
- El problema 1 está terminado, ya que no quedan más dígitos en el divisor para arrastrar. Arriba de la barra de división está la respuesta (13).
-
7Repite el proceso de división larga (problema de ejemplo 2). Tal como lo has hecho anteriormente, primero divides, luego multiplicas y por último restas.[6]
- Para 3厂136: determina cuántas veces cabe 3 en 13, escribe la respuesta (4) a la derecha del 0 que está arriba de la barra de división. Luego multiplica 4 por 3 y escribe la respuesta (12) debajo del 13. Finalmente, réstale 12 a 13 y escribe la respuesta (1) debajo del 12.
-
8Haz otra ronda de división larga para obtener el resto (problema de ejemplo 2). Una vez que hayas terminado el problema, deberás fijarte si hay un resto (esto es, si queda un número al finalizar los cálculos). Este resto va al lado del número entero que has obtenido como respuesta.[7]
- Para 3厂136: continúa con el proceso con otra ronda más. Baja el 6 del 136 para formar 16 en la fila inferior. Divide 16 entre 3 y escribe el resultado (5) arriba de la línea de división. Multiplica 5 por 3 y escribe el resultado (15) en una nueva fila más abajo. Réstale 15 al 16 y escribe el resultado (1) en una nueva fila más abajo.
- Como ya no quedan más dígitos para arrastrar hacia abajo en el dividendo, ya has terminado de resolver el problema y el 1 de la línea inferior es el resto (el número que sobra). Escríbelo arriba de la barra de división con una "R" adelante. Así, la respuesta final será "45 R 1".
Anuncio
Método 2
Método 2 de 5:División corta
-
1Utiliza una barra de división para escribir el problema. Coloca el divisor, que es el número entre el cual vas a dividir, afuera (y a la izquierda) de la barra de división. Coloca el dividendo, que es el número a dividir, dentro (a la derecha y debajo) de la barra de división.[8]
- Para poder hacer una división corta, el divisor no debe tener más de un dígito.
- Problema de ejemplo: 518 ÷ 4. En este caso el 4 va afuera de la barra de división y el 518 dentro de ella.
-
2Divide el primer dígito del dividendo entre el divisor. En otras palabras, determina cuántas veces cabe el número que está afuera de la barra de división en el primer dígito del número que está adentro de ella. Escribe el número entero que has obtenido como resultado arriba de la barra de división y escribe el resto (el número que sobra) como superíndice junto al primer dígito del dividendo.[9]
- En el problema de ejemplo, 4 (el divisor) cabe en 5 (el primer dígito del dividendo) 1 vez, con un resto de 1 (5 ÷ 4 = 1 R 1). Coloca el cociente, 1, arriba de la barra de división larga. Coloca un 1 pequeño (superíndice) junto al 5 para recordarte a ti mismo que tenías un resto de 1.
- El 518 debajo de la barra ahora deberá quedar así: 5118.
-
3Divide el resto y el segundo dígito del dividendo entre el divisor. Haz de cuenta que el número que has escrito como superíndice (que representa al resto) es un número completo y combínalo con el dígito del dividendo que está justo a su derecha. Determina cuántas veces cabe el divisor en este nuevo número de dos dígitos y escribe el número entero que has obtenido como respuesta y el resto tal como lo has hecho en el paso anterior.[10]
- En el problema de ejemplo, el número formado por el resto y el segundo número del dividendo es 11. El divisor, 4, cabe dos veces en 11 con un resto de 3 (11 ÷ 4 = 2 R 3). Escribe el 2 arriba de la línea de división (formando 12) y el 3 como superíndice junto al 1 de 518.
- El dividendo original, 518 ahora quedará así: 51138.
-
4Repite el proceso hasta que hayas terminado con todos los dígitos del dividendo. Sigue determinando cuántas veces cabe el divisor en el número formado por el dígito siguiente del dividendo y el superíndice del resto que está inmediatamente a su izquierda. Una vez que hayas trabajado con todos los dígitos del dividendo, obtendrás la respuesta final.[11]
- En el problema de ejemplo, el próximo (y último) número del dividendo es 3 (el 3 que has obtenido como resto en el paso anterior) y el 8 que corresponde al último término del dividendo. El divisor, 4, cabe nueve veces en 38 con un resto de 2 ('38 ÷ 4 = 9 R 2) porque 4 x 9 = 36, o sea que faltan 2 para 38. Anota este resto final (2) arriba de la barra de división para completar la respuesta.
- Así, la respuesta final arriba de la barra de división será 129 R 2.
Anuncio
Método 3
Método 3 de 5:Dividir fracciones
-
1Escribe la ecuación de modo que las dos fracciones queden una al lado de la otra. Para dividir fracciones, simplemente escribe la primera fracción seguida del símbolo de la división (÷) y luego la segunda. [12]
- El problema podría ser, por ejemplo, 3/4 ÷ 5/8. Por comodidad, es mejor separar el numerador (número de arriba) del denominador (número de abajo) con líneas horizontales en vez de diagonales en cada fracción.
-
2Invierte el numerador y el denominador en la segunda fracción. Así convertirás la segunda fracción en su recíproca.[13]
- Siguiendo con el problema de ejemplo, invierte 5/8 de modo que el 8 quede arriba y el 5 abajo.
-
3Cambia el signo de la división por uno de multiplicación. Para dividir fracciones, hay que multiplicar la primera por la recíproca de la segunda.[14]
- Por ejemplo: 3/4 x 8/5.
-
4Multiplica los numeradores de las fracciones. Sigue el mismo procedimiento que usarías para multiplicar 2 fracciones cualesquiera.[15]
- En este caso, los numeradores son 3 y 8; por lo tanto, debes calcular 3 x 8 = 24.
-
5Multiplica del mismo modo los denominadores de las fracciones. Una vez más, el procedimiento es exactamente el mismo que usarías para multiplicar 2 fracciones cualesquiera.[16]
- En el problema de ejemplo, los denominadores son 4 y 5; por lo tanto, debes calcular 4 x 5 = 20.
-
6Coloca el producto de los numeradores sobre el producto de los denominadores. Ahora que has multiplicado numeradores y denominadores de ambas fracciones, puedes formar el producto entre ambas.[17]
- Así, en el problema de ejemplo, 3/4 x 8/5 = 24/20.
-
7Reduce la fracción si es necesario. Para reducir la fracción, debes encontrar el máximo común divisor (el número más grande que puede dividir los dos números sin dejar resto) y dividir tanto el numerador como el denominador entre ese número.[18]
- En el caso de 24/20, el número más grande que puede dividir tanto 24 como 20 es 4. Para confirmarlo, puedes escribir todos los factores de estos números y elegir el mayor factor de ambos:
- 24: 1, 2, 3, 4, 6, 8, 12, 24
- 20: 1, 2, 4, 5, 10, 20
- Como 4 es el máximo común divisor de 24 y 20, divide ambos números entre 4 para reducir la fracción.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5. Por lo tanto, 3/4 ÷ 5/8 = 6/5
- En el caso de 24/20, el número más grande que puede dividir tanto 24 como 20 es 4. Para confirmarlo, puedes escribir todos los factores de estos números y elegir el mayor factor de ambos:
-
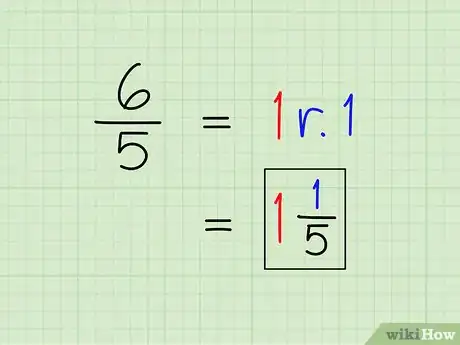
8Reescribe la fracción como un número mixto si es necesario. Para hacerlo, divide el numerador entre el denominador y escribe la respuesta como un número entero. El resto, o número que sobra, será el numerador de la nueva fracción. El denominador de la fracción seguirá siendo el mismo.[19]
- En el problema de ejemplo, 5 cabe una vez en 6 con un resto de 1. Por lo tanto, el nuevo número entero será 1, el nuevo numerador será 1 y el denominador seguirá siendo 5.
- Como resultado, 6/5 = 1 1/5.
Anuncio
Método 4
Método 4 de 5:Dividir exponentes
-
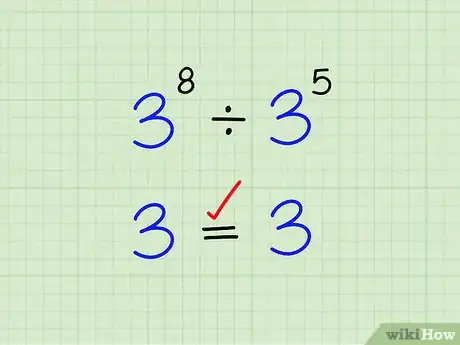
1Asegúrate de que los exponentes tengan la misma base. Solo es posible dividir números con exponentes si estos tienen la misma base. Si no tienen la misma base, tendrás que manipularlos hasta que la tengan (si es posible). [20]
- Como principiante lo mejor es empezar con un problema de ejemplo en el cual ambos números ya tienen la misma base, por ejemplo 38 ÷ 35.
-
2Resta los exponentes. Ahora simplemente réstale el segundo exponente al primero. No te preocupes por la base por ahora.[21]
- En el problema de ejemplo: 8 - 5 = 3.
-
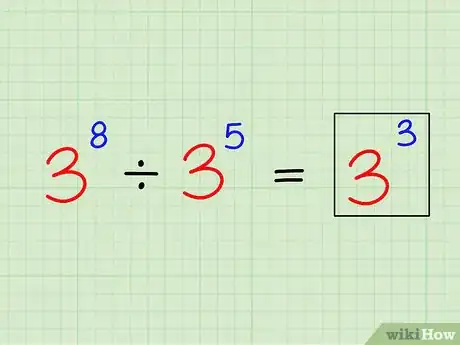
3Coloca el nuevo exponente arriba de la base original. Ahora simplemente escribe el nuevo exponente arriba de la base original. ¡Eso es todo![22]
- Por lo tanto: 38 ÷ 35 = 33.
Anuncio
Método 5
Método 5 de 5:Dividir decimales
-
1Escribe el problema utilizando la barra de la división larga. Coloca el divisor, que es el número entre el cual dividirás, afuera (y a la izquierda) de la barra de división; y el dividendo, que es el número a dividir, dentro de la barra de división larga. Para dividir decimales, primero tienes que convertirlos en números enteros.[23]
- En el ejemplo 65,5 ÷ 0,5, 0,5 va afuera de la barra de división y 65,5 dentro de esta.
-
2Mueve la coma decimal tantas posiciones como sea necesario para crear dos números enteros. Simplemente desliza la coma decimal a la derecha hasta llegar al final de cada número. Ten en cuenta que debes moverla la misma cantidad de veces para ambos números. Si tienes que mover la coma decimal 2 lugares en el divisor, entonces haz lo mismo en el dividendo.[24]
- En el problema de ejemplo, solo hay que mover la coma decimal un lugar tanto en el divisor como en el dividendo. Así, 0,5 se transformará en 5 y 65,5 en 655.
- Sin embargo, si el problema de ejemplo tuviera los números 0,5 y 65,55, deberás mover la coma decimal dos lugares en 65,55 para transformarlo en 6555. En consecuencia, también tendrías que mover dos lugares en 0,5. Para hacerlo, deberás agregar un 0 al final, con lo cual el número se transformaría en 50.
-
3Alinea la coma decimal correctamente arriba de la barra de división. Coloca una coma decimal en la barra de división larga, justo arriba del decimal en el dividendo.[25]
- En el problema de ejemplo, el decimal de 655 aparecería después del último 5 (como 655,0). Por lo tanto, escribe la coma decimal arriba de la línea de división, justo arriba de donde aparecería la coma decimal de 655.
-
4Resuelve el problema siguiendo los pasos de una división larga. Para dividir 655 entre 5, haz lo siguiente:[26]
- Divide el dígito de las centenas, 6, entre 5. Obtendrás 1 con un resto de 1. Coloca 1 en el lugar de las centenas arriba de la barra de división larga y réstale 5 al 6 debajo del número 6.
- El resto, 1, queda así. Arrastra el primer 5 de 655 hacia abajo para crear el número 15. Divide 15 entre 5 y obtendrás 3. Coloca ese 3 arriba de la barra de división larga, junto al 1.
- Arrastra el último 5. Divide 5 entre 5 y obtendrás 1. Coloca ese 1 arriba de la barra de división larga. No queda ningún resto, ya que 5 cabe exactamente 1 vez en 5.
- La respuesta es el número que está arriba de la barra de división larga (131). Por lo tanto, 655 ÷ 5 = 131. Si tomas una calculadora, verás que esta también es la respuesta al problema de división original 65,5 ÷ 0,5.
Anuncio
Vídeo
Referencias
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ https://www.k5learning.com/blog/step-step-guide-long-division
- ↑ http://www.bbc.co.uk/skillswise/factsheet/ma12pape-l1-f-short-division
- ↑ http://www.bbc.co.uk/skillswise/factsheet/ma12pape-l1-f-short-division
- ↑ http://www.bbc.co.uk/skillswise/factsheet/ma12pape-l1-f-short-division
- ↑ http://www.bbc.co.uk/skillswise/factsheet/ma12pape-l1-f-short-division
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/fractions_division.html
- ↑ http://www.mathsisfun.com/algebra/variables-exponents-multiply.html
- ↑ http://www.mathsisfun.com/algebra/variables-exponents-multiply.html
- ↑ http://www.mathsisfun.com/algebra/variables-exponents-multiply.html
- ↑ https://www.mathsisfun.com/dividing-decimals.html
- ↑ https://www.mathsisfun.com/dividing-decimals.html
- ↑ https://www.mathsisfun.com/dividing-decimals.html
- ↑ https://www.mathsisfun.com/dividing-decimals.html
Acerca de este wikiHow
Para hacer una división simple piensa cuántas veces cabe un número dentro de otro. Por ejemplo, 6 ÷ 2 es 3 porque 3 cabe 2 veces en el número 6. Si el número es grande, es mejor que te tomes un tiempo para revisar las tablas de multiplicar. Para hacer una división larga escribe debajo de la barra de división el número que quieras dividir y fuera de la barra el número por el cual vas a dividirlo. Por ejemplo, si quieres calcular 72 ÷ 3, coloca el 72 debajo de la barra de división y el 3 afuera. Luego calcula cuántas veces cabe 3 en el primer número que está debajo de la barra. En este caso, se calcula cuántas veces cabe 3 en 7. La respuesta es 2, con 1 restante. Escribe el número 2 arriba de la barra y el resto (en este caso 1) debajo del 7. Luego, si hay más números debajo de la barra de división, bájalos a la misma altura que el resto. Así, en este caso, debes bajar el 2 y ponerlo al lado del 1 para formar 12. Luego repite el proceso: ¿cuántas veces cabe 3 en el número 12? En este ejemplo, 3 cabe cuatro veces en 12. Por lo tanto, debes escribir 4 en la línea de arriba del problema, al lado de los otros números. De este modo, 72 ÷ 3 = 24. Si quieres aprender a dividir fracciones, ¡sigue leyendo este artículo!

















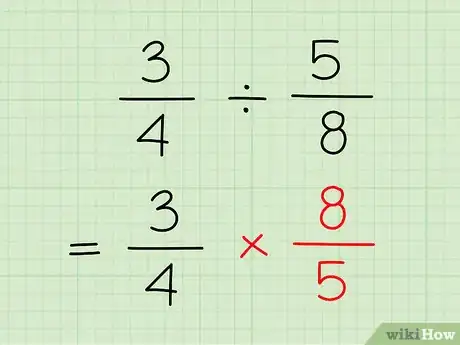


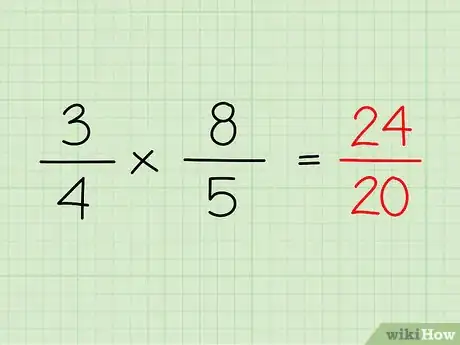

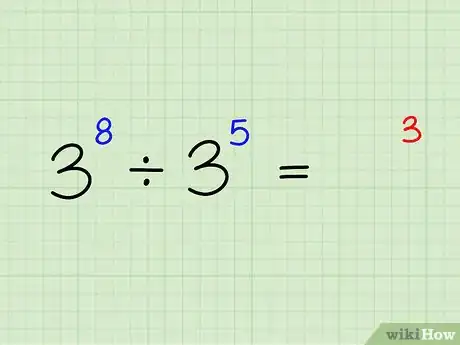



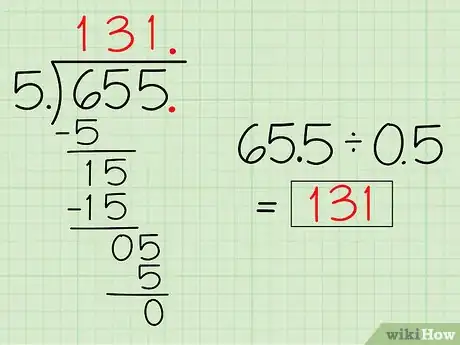



















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 168 691 veces.