Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 7 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 40 131 veces.
Un rombo es una figura de 4 lados con muchas propiedades diferentes.[1] Estas te permiten emplear numerosos métodos para hallar el perímetro. Dado que todos los lados son iguales, solo necesitas saber la medida de uno de ellos para hacerlo. Sin embargo, también puedes aplicar geometría o trigonometría para hallar el perímetro sin conocer la medida de los lados del rombo.
Pasos
Método 1
Método 1 de 3:Utilizar la longitud de un lado
-
1Utiliza la fórmula para hallar el perímetro de un rombo. Dado que, por definición, los cuatro lados de un rombo miden lo mismo, la fórmula para hallar su perímetro es , donde es el perímetro y representa la longitud de un lado.[2]
- También puedes utilizar la fórmula , ya que el perímetro de un polígono es la suma de todos sus lados.[3]
- Si sabes que no todos los lados miden lo mismo, la figura no es un rombo y no puedes aplicar esta fórmula.
- Si no conoces la longitud de ninguno de los lados del rombo, no puedes utilizar este método.
- Un cuadrado es un tipo especial de rombo que tiene cuatro ángulos de 90 grados.
-
2Coloca la longitud del lado del rombo en la fórmula. Asegúrate de sustituir la variable .
- Por ejemplo, si sabes que uno de los lados del rombo mide 4 metros, tu fórmula se verá así: .
-
3Resuelve la ecuación para hallar . Para hacerlo, multiplica por 4.
- Por ejemplo:
Por lo tanto, el perímetro del rombo es .
Anuncio - Por ejemplo:
Método 2
Método 2 de 3:Utilizar la longitud de las diagonales
-
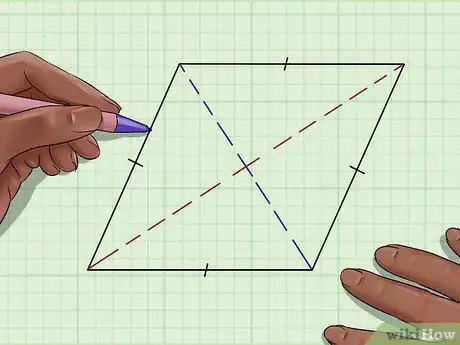
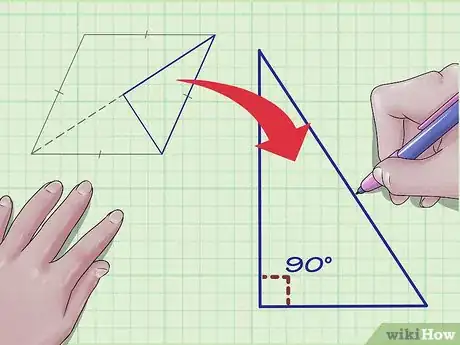
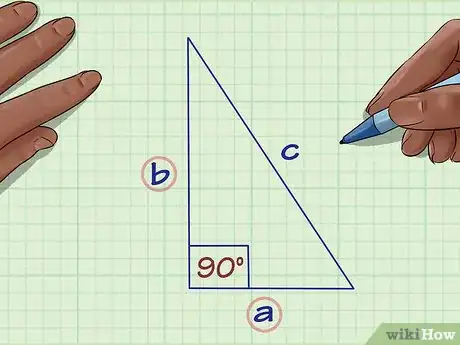
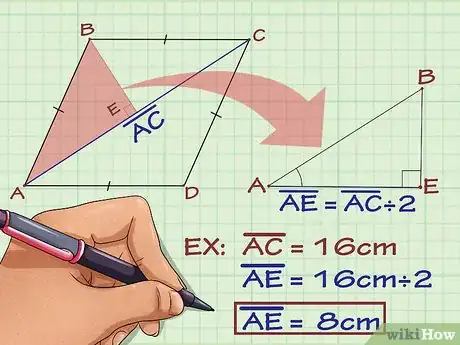
1Nota que las dos diagonales del rombo crean cuatro triángulos congruentes. Delinea uno de ellos. Este te servirá para hallar la longitud de uno de los lados del rombo.
- Dado que los triángulos son congruentes, no importa cuál elijas.
-
2Identifica el ángulo de 90 grados del triángulo. Las dos diagonales del rombo son perpendiculares, así que el ángulo central del triángulo será de 90 grados.[4]
-
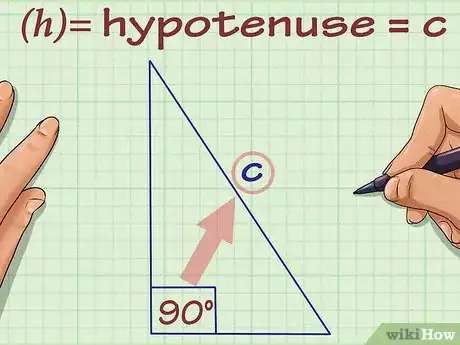
3Asigna una variable a la hipotenusa del triángulo. La hipotenusa es el lado opuesto al ángulo de 90 grados.[5] Por tradición, la variable que identifica la longitud de la hipotenusa es .
- La hipotenusa del triángulo es uno de los lados del rombo. Por lo tanto, si hallas , sabrás la longitud de uno de los lados del rombo.
-
4Asigna una variable a cada lado del triángulo. Normalmente, se emplean las variables y .
-
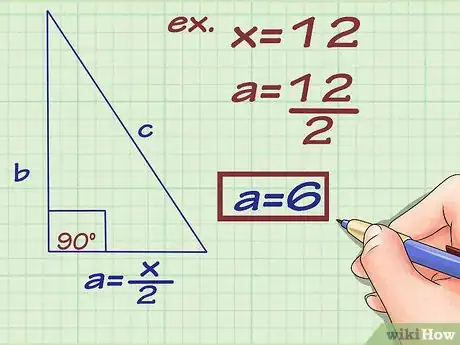
5Halla la longitud del lado . Para hacerlo, divide la longitud de la diagonal por donde pasa entre 2. Coloca la medida del lado en el triángulo.
- Dado que las diagonales de un rombo se bisecan entre sí, se sabe que la longitud de los segmentos a cada lado de la intersección miden lo mismo.[6] Ya que el lado mide la mitad de lo que mide la diagonal, puedes dividir la longitud de la diagonal por la mitad para calcular su tamaño.
- Por ejemplo, si el lado es parte de una diagonal que mide 12 metros, puedes hallar la longitud del lado de la siguiente manera:
-
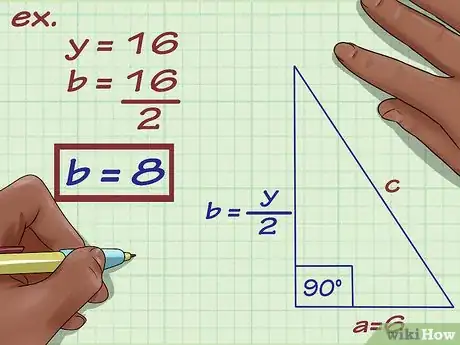
6Halla la longitud del lado . Para hacerlo, divide la longitud de la diagonal por donde pasa el lado entre 2. Coloca la medida del lado en el triángulo.
- Por ejemplo, si el lado es parte de una diagonal que mide 16 metros, puedes hallar la longitud del lado de la siguiente manera:
- Por ejemplo, si el lado es parte de una diagonal que mide 16 metros, puedes hallar la longitud del lado de la siguiente manera:
-
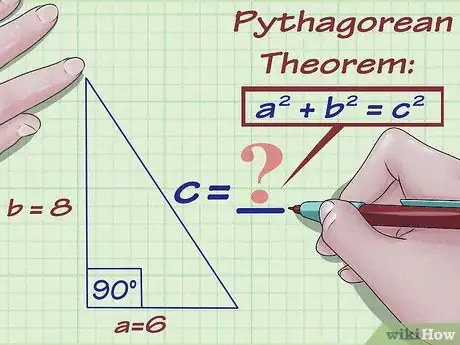
7Aplica el teorema de Pitágoras. El teorema plantea que . Esta es una fórmula geométrica básica que se emplea para hallar la longitud de los lados de un triángulo rectángulo.
-
8Reemplaza los valores conocidos del triángulo en la fórmula del teorema de Pitágoras. Asegúrate de sustituir el valor de y , pero no te preocupes por el orden; este no se ve afectado debido a la propiedad conmutativa.
- Por ejemplo, si y , la ecuación se verá así: .
-
9Resuelve la ecuación para hallar . Para hacerlo, tendrás que elevar y al cuadrado, sumar los resultados y hallar la raíz cuadrada del total.
- Por ejemplo:
- Por ejemplo:
-
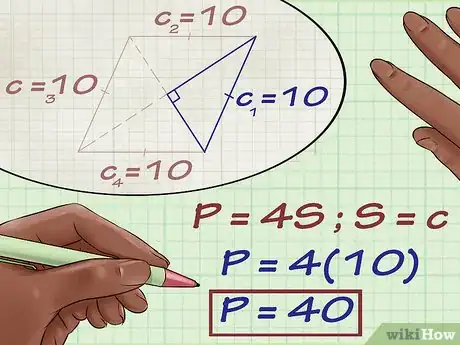
10Multiplica por 4. Dado que la hipotenusa también es uno de los lados del rombo, para hallar el perímetro del rombo tendrás que reemplazar el valor de en la fórmula para hallar el perímetro del rombo, que es , donde representa la longitud de uno de los lados del rombo. En este caso, su valor es el mismo que el de .
- Por ejemplo:
- Por ejemplo:
-
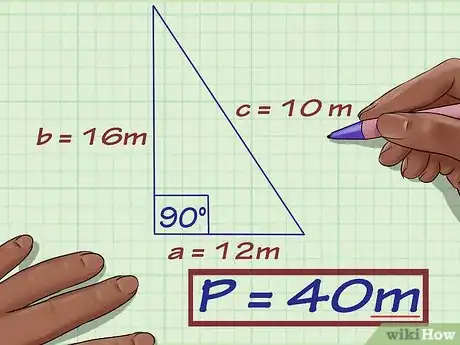
11Escribe tu respuesta final. No olvides incluir la unidad de medida correcta.
- Por ejemplo, el perímetro de un rombo cuyas diagonales miden 12 y 16 metros es 40 metros.
Anuncio
Método 3
Método 3 de 3:Utilizar una diagonal y un ángulo
-
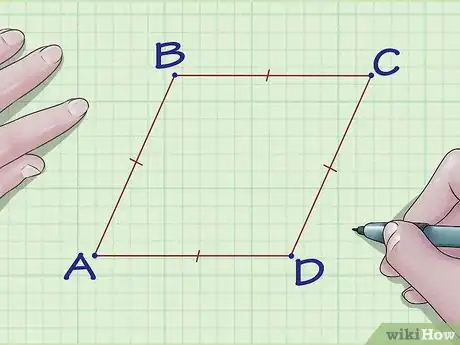
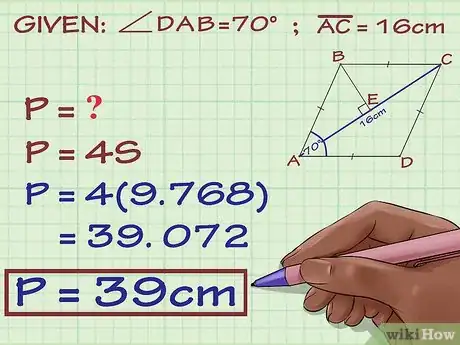
1Asigna una variable a los vértices del rombo si es que aún la tienen. No importa cuáles utilices.
- Los vértices (en singular, el vértice) son las esquinas del rombo.
- Por ejemplo, podrías etiquetar cada vértice con las variables , , y .
-
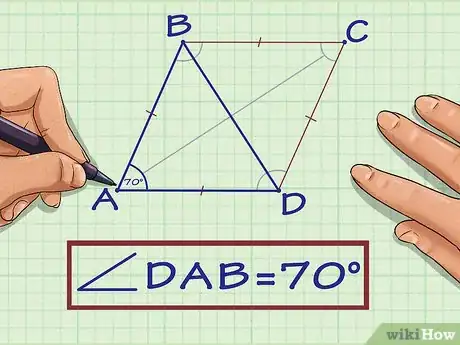
2Nota que las dos diagonales del rombo crean cuatro triángulos congruentes. Delinea uno de ellos. Este te servirá para hallar la longitud de uno de los lados del rombo.
- Dado que los triángulos son congruentes, no importa cuál elijas. Sin embargo, para facilitar tu trabajo, será mejor que utilices el que comparte un ángulo del rombo que conoces.
- Por ejemplo, si sabes que el ángulo del rombo tiene 70 grados, lo ideal es delinear un triángulo que incluya el punto A.
-
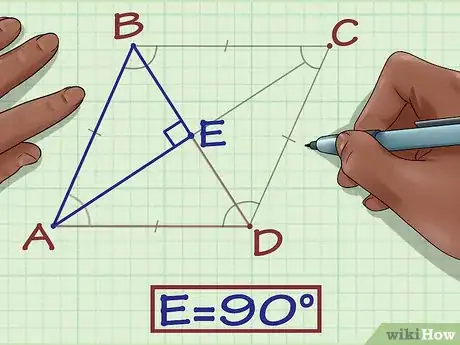
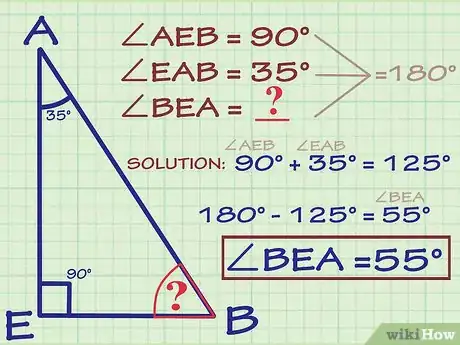
3Identifica el ángulo de 90 grados del triángulo. Las dos diagonales de un rombo son perpendiculares, de modo que el ángulo central del triángulo será de 90 grados.[7] Si aún no le has asignado una variable al ángulo, utiliza .
-
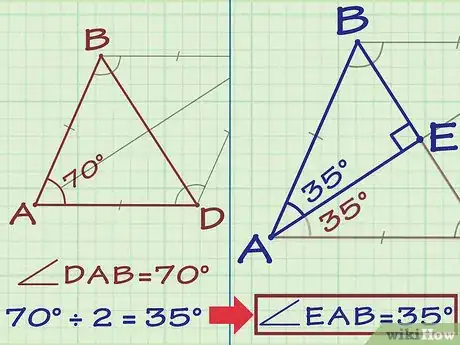
4Determina el valor del ángulo . Recuerda que las diagonales de un rombo bisecan sus vértices.[8] Por tanto, si conoces el ángulo del rombo, divídelo por la mitad para hallar el ángulo del triángulo. Coloca los grados de dicho ángulo en el triángulo.
- Este método no funcionará si no conoces el ángulo de al menos uno de los vértices del rombo.
- Por ejemplo, si sabes que el ángulo del rombo es 70 grados, entonces el ángulo del triángulo es la mitad, es decir, 35 grados.
-
5Determina el valor del ángulo faltante. Recuerda que los ángulos interiores de un triángulo sumados darán un total de 180 grados.[9] Por tanto, si conoces la medida de dos ángulos, puedes restarlos del total para hallar la medida del tercer ángulo. Coloca los grados del ángulo en el triángulo.
- Por ejemplo, si sabes que el ángulo es de 90 grados y el ángulo es de 35 grados, para hallar el tercer ángulo tendrás que sumar los ángulos que ya conoces y restar el total de 180.
Por lo tanto, el ángulo es 55 grados.
- Por ejemplo, si sabes que el ángulo es de 90 grados y el ángulo es de 35 grados, para hallar el tercer ángulo tendrás que sumar los ángulos que ya conoces y restar el total de 180.
-
6Determina la longitud de uno de los lados del triángulo. Para hacerlo, divide la longitud de la diagonal por donde pasa uno de los lados del triángulo entre 2. Coloca la medida del lado en el triángulo.
- Dado que las diagonales de un rombo se bisecan entre sí, se sabe que la longitud de los segmentos a cada lado de la intersección miden lo mismo.[10]
- Este método no funcionará si no conoces la longitud de al menos una de las diagonales del rombo.
- Por ejemplo, si sabes que la diagonal mide 16 centímetros, puedes dividir 16 por la mitad para hallar la longitud del lado del triángulo. ; por lo tanto, el lado mide .
-
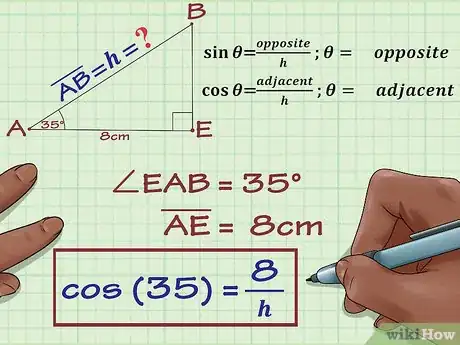
7Utiliza la proporción del seno o del coseno. La opción que elijas dependerá qué lado y qué ángulo conozcas. Si necesitas más información sobre el tema, revisa el artículo Cómo utilizar el ángulo recto en trigonometría.
- Si conoces la longitud del lado opuesto al ángulo, utiliza el seno. Aplica la fórmula , donde es el ángulo que conoces, “Opuesto” se refiere a la longitud del lado opuesto al ángulo y es la longitud de la hipotenusa.
- Si conoces la longitud del lado adyacente al ángulo, utiliza el coseno. Aplica la fórmula , donde es el ángulo que conoces, “Adyacente” se refiere a la longitud del lado adyacente al ángulo y es la longitud de la hipotenusa.
- Por ejemplo, si sabes que el ángulo del triángulo es 35 grados y el lado adyacente mide 8 centímetros, puedes utilizar el coseno:
-
8Resuelve la fórmula proporcional para hallar la longitud de la hipotenusa. Esta también es la longitud de uno de los lados del rombo, así que necesitas esta medida para hallar el perímetro del rombo.
- Por ejemplo:
Por lo tanto, la longitud de la hipotenusa, que también es el lado es aproximadamente 9,768.
- Por ejemplo:
-
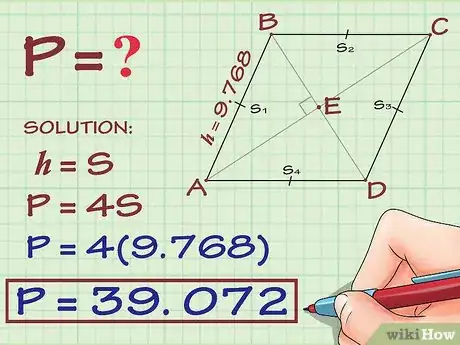
9Multiplica la longitud de la hipotenusa por 4. Dado que la hipotenusa también es uno de los lados del rombo, para hallar su perímetro tendrás que reemplazar el valor de en la fórmula para hallar el perímetro de un rombo, que es , donde representa la longitud de uno de los lados del rombo. En este caso, es el mismo valor que hallaste para .
- Por ejemplo:
- Por ejemplo:
-
10Escribe la respuesta final. Esta será un valor aproximado, ya que la medida del seno o el coseno es redondeada. No olvides incluir la unidad de medida correcta.
- Por ejemplo, el perímetro de un rombo con un ángulo de 70 grados y una diagonal de 16 centímetros es 39 centímetros.
Anuncio
Consejos
- Puedes sumar las longitudes de los lados para hallar el perímetro de cualquier polígono; un triángulo, un rectángulo, un pentágono u otra figura de lados rectos. Los círculos y otras figuras curvas requieren otras fórmulas.
Referencias
- ↑ http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rhombus.php
- ↑ http://www.mathopenref.com/rhombusperimeter.html
- ↑ http://www.mathopenref.com/polygonperimeter.html
- ↑ http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rhombus.php# diagonalRhombus
- ↑ http://mathworld.wolfram.com/Hypotenuse.html
- ↑ https://www.mathsisfun.com/geometry/parallelogram.html#Perimeter
- ↑ http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rhombus.php# diagonalRhombus
- ↑ http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rhombus.php
- ↑ http://www.mathopenref.com/triangleinternalangles.html









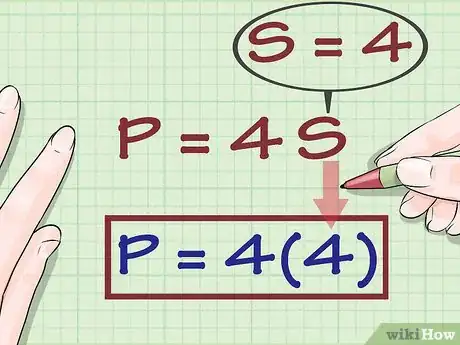













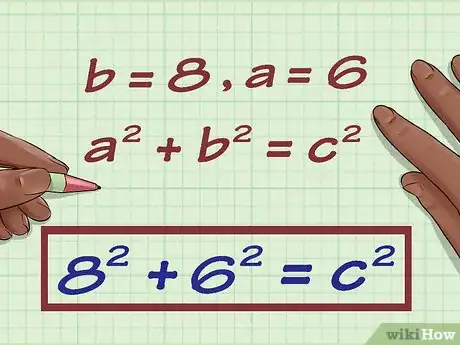

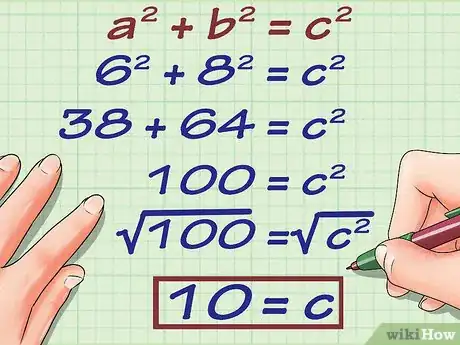






















































wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 40 131 veces.