wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 11 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 150 972 veces.
La integración constituye la operación inversa a la derivación. Suele decirse que, si bien la derivación es una ciencia, la integración es un arte. Esto se debe simplemente a que esta última es más difícil, ya que las derivadas solo tienen relación con el comportamiento de una función en un punto, mientras que, para las integrales, dado que son sumas glorificadas, es necesario tener un conocimiento global de la función. Existen algunas funciones cuyas integrales pueden evaluarse mediante las técnicas estándar que se mencionan en este artículo, pero, para muchas más de ellas, esto no es así.
En este artículo, repasaremos las técnicas básicas de la integración con una sola variable y las aplicaremos a las funciones que contengan antiderivadas.
Pasos
Parte 1
Parte 1 de 7:Conceptos básicos
-
1Comprende la notación de las integrales. Una integral consiste en cuatro partes:
- El símbolo representa la integración y, en realidad, es una S alargada.
- A la función se le llama la función original cuando se encuentra dentro de la integral.
- La derivada expresa de forma intuitiva la variable que se integra respecto a x. La integración (de Riemann) constituye apenas una suma de rectángulos infinitesimalmente delgados cuya altura mide , por lo que se puede observar que hace referencia al ancho de estos rectángulos.
- Las letras y constituyen los límites. No es necesario que una integral los tenga. Cuando no los tiene, se dice que es una integral indefinida, mientras que, cuando los tiene, se dice que es una integral definida.
- En este artículo, repasaremos el proceso de encontrar las antiderivadas de una función. Estas son funciones cuya derivada es la función original.
-
2Comprende cuál es la definición de una integral. Al referirnos a las integrales, por lo general hablamos de las integrales de Riemann, es decir, la suma de rectángulos. Si se da una función , un rectángulo cuyo ancho sea y un intervalo de , el área del primer rectángulo se obtiene mediante debido a que esto constituye simplemente la base por la altura (el valor de la función). De forma similar, el área del segundo rectángulo equivale a . Para generalizar, se dice que el área del rectángulo ith es igual a . Esto puede representarse de la siguiente forma en la notación sumatoria:
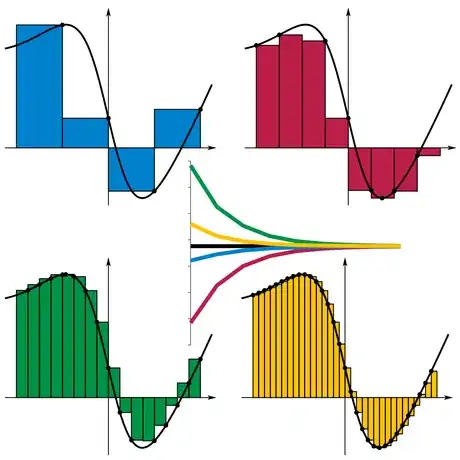
- Este símbolo de sumatoria podría asustarte si es la primera vez que lo ves, pero en realidad no es complicado. Lo único que expresa es la suma del área de rectángulos. (La variable se conoce como un índice mudo). Sin embargo, como podrás imaginar, el área de todos los rectángulos diferirá ligeramente del área verdadera, lo cual se resuelve haciendo que la cantidad de rectángulos tienda hacia el infinito. Conforme incrementa la cantidad de rectángulos, el área de todos ellos aproxima de una mejor forma el área debajo de la curva. Esto es lo que se muestra en el diagrama anterior (lee la sección "Consejos" para saber lo que se muestra en el gráfico del centro). El límite es lo que se define como la integral de la función de a .
- Por supuesto que, para que la integral tenga un significado, es necesario que el límite exista. Si no existe tal límite en el intervalo, se dice que la función no tiene una integral en el intervalo . En este artículo (así como también en casi todas las aplicaciones físicas), solo abordaremos las funciones con integrales que sí existan.
-
3No olvides colocar al evaluar las integrales indefinidas. Entre los errores más comunes que las personas cometen se encuentra el olvidarse de añadir la constante de integración. Esta es necesaria debido a que las antiderivadas no son únicas. De hecho, puede haber una cantidad infinita de antiderivadas en una misma función, lo cual está permitido porque la derivada de una constante es 0.
Parte 2
Parte 2 de 7:La regla de potencias
-
1Considera el monomio .
-
2Lleva a cabo la regla de potencias para las integrales. Esta constituye la misma regla de potencias que para las derivadas excepto a la inversa. La potencia se incrementa por 1 y dividimos entre esta nueva potencia. Recuerda añadir la constante de integración .
- Si quieres verificar si es que la regla se sostiene, deriva la antiderivada para obtener la función original.
- La regla de potencias aplica para todas las funciones de este tipo cuyo exponente sea excepto cuando . Más adelante veremos por qué.
-
3Aplica la linealidad. La integración es una operación lineal. Esto quiere decir que la integral de una suma es igual a la suma de las integrales y se puede excluir el coeficiente de cada término de la siguiente forma:
- Esto podría serte conocido debido a que la derivada también es una operación lineal: la derivada de una suma es igual a la suma de las derivadas.
- La linealidad no aplica únicamente para las integrales de los polinomios sino también para cualquier integral en donde la función que vaya a integrarse constituya una suma de dos o más términos.
-
4Encuentra la antiderivada de la función . Este es un polinomio. Por tanto, puedes calcular con facilidad la antiderivada si empleas la propiedad de linealidad y la regla de potencias. Para encontrar la antiderivada de una constante, debes tener en cuenta que . Por tanto, la constante en realidad es igual al coeficiente de .
-
5Encuentra la antiderivada de la función . Si bien esta podría parecer una función que desafíe nuestras reglas, al observarla, notarás que la fracción puede separarse en tres fracciones y se puede encontrar la antiderivada aplicando la linealidad y la regla de potencias.
- El tema común es que se deben realizar manipulaciones para poder convertir la integral en un polinomio. A partir de ahí, será fácil integrar. La habilidad recae en poder determinar si la integral es lo suficientemente fácil como para aplicar la fuerza bruta o si será necesario emplear primero la manipulación algebraica.
Parte 3
Parte 3 de 7:La integración definida
-
1Considera la integral a continuación. A diferencia de lo que ocurrió en el proceso de integración en la parte 2, también debes evaluarla en los límites.
-
2Emplea el teorema fundamental del cálculo. Este teorema consiste de dos partes. La primera se mencionó en la primera oración de este artículo: la integración constituye la operación inversa a la derivación, por lo que, al integrar una función y luego derivarla, se obtiene la función original. La segunda parte del teorema es como sigue:
- Imagina que es una antiderivada de . Por tanto, .
- Este teorema es de enorme utilidad debido a que simplifica la integral y quiere decir que la integral definida está completamente determinada solo por los valores de los límites. Ya no es necesario sumar los rectángulos para calcular las integrales, sino que solo debes encontrar las antiderivadas y evaluarlas en los límites.
-
3Evalúa la integral que figura en el paso 1. Una vez que tengas el teorema fundamental como una herramienta para la resolución de integrales, puedes calcular con facilidad el valor de la integral como se definió anteriormente.
- Nuevamente, el teorema fundamental del cálculo no solo aplica para las funciones como . Puedes emplear este teorema para integrar cualquier función con tal que puedas encontrar una antiderivada.
-
4Evalúa la integral intercambiando los límites. Observa lo que ocurre a continuación:
- Se obtuvo el negativo de la respuesta que se obtuvo antes, lo cual ilustra una propiedad importante de las integrales definidas: al intercambiar los límites, la integral se vuelve negativa.
Parte 4
Parte 4 de 7:Las antiderivadas de las funciones comunes
-
1Memoriza las antiderivadas de las funciones exponenciales. Los siguientes pasos presentan una lista de las funciones que puedes encontrar con frecuencia, como las funciones exponenciales y trigonométricas. Debido a que todas ellas pueden encontrarse ampliamente, es fundamental conocer sus antiderivadas para desarrollar tus habilidades para la integración. No olvides que a las integrales indefinidas se les debe sumar una adicional debido a que la derivada de una constante es igual a 0.
-
2Memoriza las antiderivadas de las funciones trigonométricas. Estas constituyen simplemente las derivadas que se aplican a la inversa y deberían serte conocidas. Los senos y cosenos aparecen con una mayor frecuencia, por lo que definitivamente debes memorizarlos. Los análogos hiperbólicos se encuentran del mismo modo, aunque con una menor frecuencia.
-
3Memoriza las antiderivadas de las funciones trigonométricas inversas. No es necesario que este también constituya un ejercicio de "memorización" debido a que la mayoría de estas antiderivadas deberían serte conocidas si estás familiarizado con las derivadas.
-
4Memoriza la antiderivada de la función recíproca. Se mencionó anteriormente que la función , o , constituía una excepción a la regla de potencias. Esto se debe a que la antiderivada de esta función es una función logarítmica.
- (En ocasiones, los autores prefieren colocar la en el numerador de la fracción de manera que esta se vea así . Debes tener en mente esta notación).
- La razón para el valor absoluto de la función logarítmica es sutil y, para poder obtener una respuesta completa, es necesario comprender más a fondo el análisis verdadero. Por el momento, simplemente debes aceptar el hecho de que los dominios se igualan cuando se añaden las barras de valor absoluto.
-
5Evalúa la siguiente integral a lo largo de los límites dados. La función original es , en donde no se conoce la antiderivada de . Sin embargo, es posible usar una identidad trigonométrica para reescribir la función original en términos de una función cuya antiderivada sí se conozca (concretamente, ).
- Puedes emplear una calculadora si es necesaria una aproximación decimal. En este caso, .
Parte 5
Parte 5 de 7:Las integrales de las funciones simétricas
-
1Evalúa la integral de una función par. Estas son funciones cuya propiedad es , lo que quiere decir que cualquier valor de podría reemplazarse por y se obtendría la misma función. Dos ejemplos de funciones pares son y la función coseno. En todos los casos, las funciones pares son simétricas alrededor del eje y.
- La función original es una función par, por lo que se la puede integrar de inmediato mediante el teorema fundamental del cálculo. Sin embargo, al observar más de cerca, te darás cuenta de que los límites son simétricos alrededor del valor , lo que quiere decir que la integral de -1 a 0 producirá los mismos valores que la integral de 0 a 1. Por tanto, puedes cambiar los límites de forma que sean de 0 a 1 y factorizar el 2.
- Si bien esto podría no parecer mucho, observarás de inmediato que se te simplifica el trabajo. Una vez que hayas encontrado la antiderivada, notarás que solo es necesario evaluarla en el punto . La antiderivada en el punto no contribuirá a la integral.
- Por lo general, si observas una función par cuyos límites sean simétricos, lleva a cabo esta simplificación para que cometas menos errores de aritmética.
-
2Evalúa la integral de una función impar. Estas son funciones cuya propiedad es , lo que quiere decir que cualquier valor de puede reemplazarse por y se obtendrá la negativa de la función original. Algunos ejemplos de funciones impares son y también las funciones seno y tangente. En todos los casos, las funciones impares son simétricas alrededor de su origen (imagina que giras 180 grados la parte negativa de la función. Esto hará que quede por encima de la parte positiva). La integral será 0 cuando los límites sean simétricos.
- Es posible evaluar directamente esta integral, pero también se puede reconocer que la función original es impar, además de que los límites son simétricos alrededor del origen, por lo que la integral es igual a 0. ¿Por qué es así? Esto se debe a que la antiderivada es par. La propiedad de las funciones pares es que . Por tanto, al evaluar los límites en los puntos y , implica de inmediato que .
- Las propiedades de estas funciones son muy contundentes para la simplificación de las integrales, pero es imperativo que los límites sean simétricos. De otro modo, será necesario evaluarlos a la antigua.
Parte 6
Parte 6 de 7:La integración por sustitución
-
1Busca en línea para aprender a realizar la integración por sustitución. Esta es una técnica de cambio de variables mediante el cual se espera obtener una integral más simple. Como se verá más adelante, esta técnica constituye la versión análoga de la regla de la cadena para las derivadas.
-
2Evalúa la integral de . ¿Qué se debe hacer cuando el exponente contiene un coeficiente? Se cambia las variables mediante la integración por sustitución. Este tipo de sustituciones resulta ser el más fácil de realizar y se emplea con tanta frecuencia que se suele omitir la sustitución. Sin embargo, aquí se mostrará todo el proceso.
-
3Elige un valor para y encuentra la . Se estableció que para así obtener una en la función original (es decir, una función cuya antiderivada se conozca). Luego, se debe reemplazar por , aunque es necesario que te asegures de monitorear los términos. En este ejemplo, , por lo que debes compensar dividiendo toda la integral entre .
-
4Evalúa y reescribe la integral en términos de la variable original. En el caso de las integrales indefinidas, deberás reescribirlas en términos de la variable original.
-
5Evalúa la siguiente integral con los límites dados. Esta integral es definida, por lo que es necesario evaluar la antiderivada en los límites. Asimismo, observarás que este es un caso de integración por sustitución en el que es necesario "sustituir hacia atrás".
-
6Elige un valor para y encuentra la . Debes asegurarte de cambiar también los límites según la sustitución. Se eligió para poder simplificar la raíz cuadrada. Por tanto, y el intervalo pasa a ser de 3 a 5. Sin embargo, después de reemplazar por , de todas formas queda una en la función original.
-
7Encuentra el valor de en términos de y sustituye. A esto se refería la sustitución hacia atrás mencionada anteriormente. La integración por sustitución no eliminó todos los términos de la función original, por lo que es necesario eliminarlos empleando la sustitución hacia atrás. Encontrarás que . Esto es lo que se obtiene después de simplificar:
-
8Expande y evalúa. Una de las ventajas de las integrales definidas es que, antes de evaluar, no tienes que reescribir la antiderivada en términos de la variable original, ya que, al hacerlo, añadirías complicaciones innecesarias.
Parte 7
Parte 7 de 7:La integración por partes
-
1Busca en línea para aprender cómo realizar la integración por partes. La fórmula para la integración por partes figura a continuación. Este método de integración tiene el principal objetivo de integrar el producto de dos funciones, por lo que constituye un método análogo a la regla del producto para las derivadas. Mediante esta técnica, se simplifica la integral hasta obtener una que con suerte será más fácil de evaluar.
-
2Evalúa la integral de la función logarítmica. Se sabe que es la derivada de pero no se conoce la antiderivada. Esta integral resulta ser una aplicación simple de la integración por partes.
-
3Elige un valor para y una y encuentra y . Se eligió debido a que la derivada es algebraica y, por tanto, su manipulación es más fácil. Entonces, , por lo que y . Esto es lo que se obtiene al sustituir todo esto en la fórmula:
- La integral de un logaritmo se convirtió en la integral de 1, cuya evaluación es trivial.
-
4Evalúa.
Consejos
- Al definir la suma de Riemann, puede significar el lado izquierdo, el lado derecho o el punto medio de en el intervalo . Cada una de estas definiciones diferentes producirá una suma ligeramente diferente del área de los rectángulos. Sin embargo, cuando la cantidad de estos tiende hacia el infinito, el error entre cualquiera de estas definiciones se iguala a 0 y todas las sumas convergen en la integral.
- Esto es lo que se muestra realmente en el diagrama del paso 2: los rectángulos azules son rectángulos del lado derecho, los amarillos son rectángulos del lado izquierdo, la muestra roja es el mínimo en el intervalo y la muestra azul es el máximo. En el gráfico del centro, se muestra que, cuando la cantidad de rectángulos tiende hacia el infinito, todas estas áreas convergen en la integral.











![[a,b]](./images/1961107370-9c4b788fc5c637e26ee98b45f89a5c08c85f7935.webp)






























































































![[x_{{i}},x_{{i}}+\Delta x]](./images/2096701515-4b5bc59be844f9c15de941deab9084b76f1ecf65.webp)






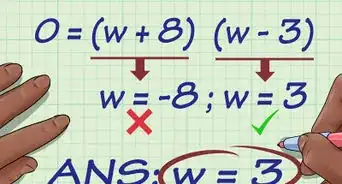

-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)




