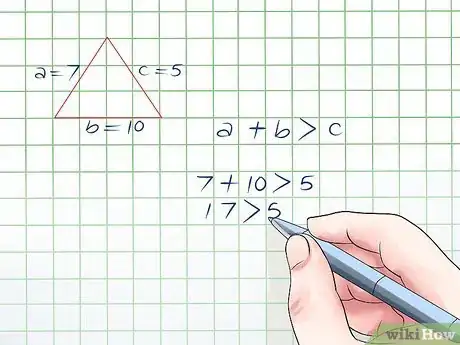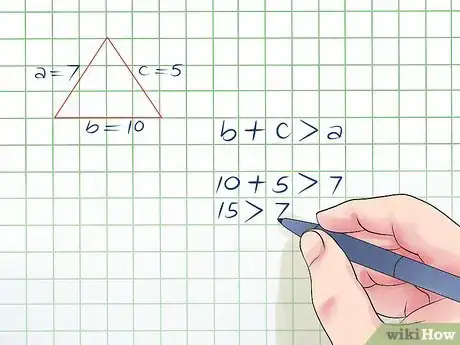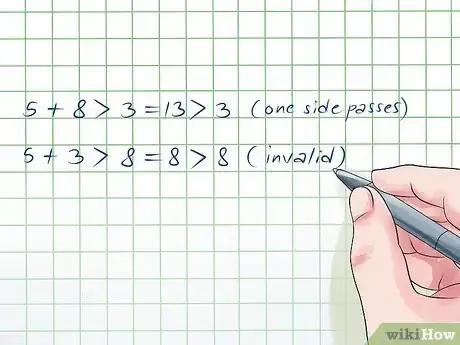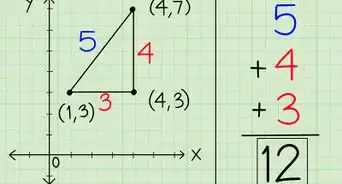Cómo saber si hay un triángulo teniendo las medidas de tres lados

Información del autor

Determinar si las medidas de tres lados forman un triángulo es más fácil de lo que parece. Lo único que debes hacer es usar el teorema de la desigualdad del triángulo, el cual establece que la suma de dos lados del triángulo siempre es mayor que la medida del tercer lado. Si esto resulta ser verdad para todas las tres combinaciones de las sumas, entonces tienes un triángulo.

Pasos

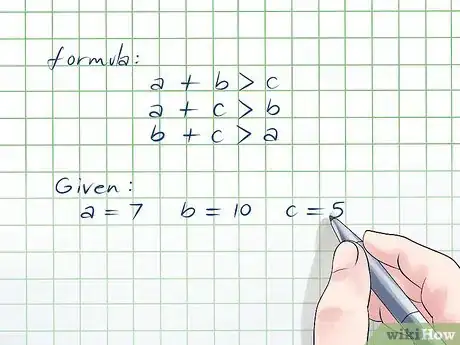
1
Aprende el teorema de la desigualdad del triángulo. Este teorema simplemente establece que la suma de dos de los lados del triángulo debe ser mayor al tercer lado. Si esto es verdad en todas las tres combinaciones, entonces si es un triángulo. Tienes que ver estas combinaciones una por una para averiguar si sí es un triángulo. Viéndolo como una fórmula, puedes establecer los lados como a, b y c, y como el teorema es una desigualdad, la fórmula quedaría: a+b > c, a+c > b y b+c > a.^{[1]
X
Fuente de investigación}
- Para este ejemplo, a = 7, b = 10, y c = 5.
2
Revisa si la suma de los primeros dos lados es mayor que el tercer lado. En este caso, puedes sumar los lados a y b, o 7 + 10, para obtener 17, lo cual es mayor que 5. También puedes verlo como 17 > 5.
3
Revisa si la suma de la siguiente combinación de los otros dos lados es mayor que el lado restante. Ahora revisa si las sumas de los lados a y c es mayor que el lado b. Esto significa que debes ver si 7 + 5, o 12, es mayor a 10. 12 > 10, así que sí lo es.
4
Revisa si la suma de la última combinación de los otros dos lados es mayor que el lado restante. Necesitas ver si la suma del lado b y el lado c es mayor que el lado a. Para hacer esto, necesitas ver si 10 + 5 es mayor que 7. 10 + 5 = 15, y 15 > 7, así que el triángulo si aprueba esta teoría.
5
Revisa tu trabajo. Ahora que ya revisaste todas las combinaciones una por una, puedes volver a revisar si esta regla es verdadera en todas las combinaciones. Si la suma de dos de los lados es mayor que el tercer lado en todas las combinaciones, como lo es para el triángulo de este ejemplo, entonces el triángulo es válido. Si la regla es inválida, aunque sea solamente en una combinación, el triángulo es inválido:
- a + b > c = 17 > 5
- a + c > b = 12 > 10
- b + c > a = 15 > 7
6
Conoce cómo identificar un triángulo inválido. Solo como práctica, asegúrate de poder identificar un triángulo inválido. Digamos que estás trabajando con estas tres medidas: 5, 8, y 3. Veamos si pasa la prueba:
- 5 + 8 > 3 = 13 > 3, un lado si lo pasa.
- 5 + 3 > 8 = 8 > 8. Con esta respuesta puedes ver que el triángulo es inválido, no tienes por qué seguir haciendo la prueba.
Anuncio