Cómo aprender trigonometría

Coescrito por Personal de wikiHow

La trigonometría es la rama de la matemática que estudia triángulos y círculos. Sus funciones se usan para describir las propiedades de cualquier ángulo, las relaciones en cualquier triángulo, y los gráficos de cualquier ciclo recurrente. Aprender trigonometría te ayudará a entender, visualizar y graficar estas relaciones y ciclos. Si combinas el estudio por tu cuenta con mantener la concentración en clase, captarás los conceptos de trigonometría básicos y probablemente comenzarás a notar los ciclos en el mundo a tu alrededor.

Método 1

Método 1 de 4:
Centrarse en las principales ideas trigonométricas

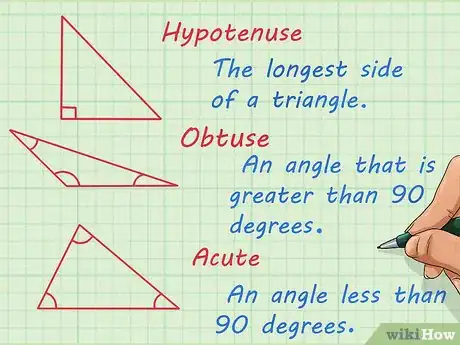
1
Define las partes de un triángulo. En su núcleo, la trigonometría es el estudio de las relaciones presentes en los triángulos. Un triángulo tiene tres lados y tres ángulos. Por definición, la suma de los ángulos de cualquier triángulo es 180 grados. Debes familiarizarte con los triángulos y su terminología para triunfar en la trigonometría. Algunos términos comunes son:^{[1]
X
Fuente de investigación}
- hipotenusa: el lado más largo de un triángulo
- obtuso: ángulo mayor a 90 grados
- agudo: ángulo menor a 90 grados
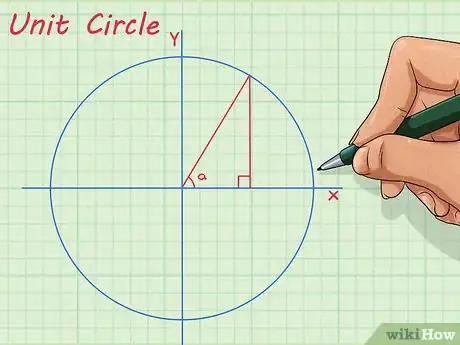
2
Aprende a hacer el radio de un círculo. Este te permite modificar la escala de cualquier triángulo para que la hipotenusa sea igual a uno. Es útil porque relaciona las funciones trigonométricas, como seno y coseno a porcentajes. Una vez que entiendas el radio de un círculo, puedes usar los valores trigonométricos de un cierto ángulo para responder preguntas sobre triángulos con esos ángulos. ^{[2]
X
Fuente de investigación}
- Ejemplo 1: el seno de 30 grados es 0,50. Esto quiere decir que el lado opuesto al ángulo de 30 grados es exactamente la mitad del largo de la hipotenusa.
- Ejemplo 2: esta relación se puede usar para encontrar el largo de la hipotenusa en un triángulo que tiene un ángulo de 30 grados con el lado opuesto a ese ángulo que mide 18 cm (7 pulgadas). La hipotenusa es igual a 36 cm (14 pulgadas).
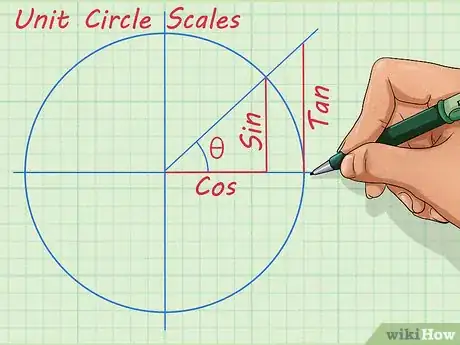
3
Aprende las funciones trigonométricas. Son seis funciones fundamentales para entender la trigonometría. Juntas, definen las relaciones entre un triángulo, y te permiten entender las propiedades únicas de cualquier triángulo. Estas seis funciones son: ^{[3]
X
Fuente de investigación}
- seno (sen)
- coseno (cos)
- tangente (tan)
- secante (sec)
- cosecante (cosec)
- cotangente (cot)
4
Conceptualiza las relaciones. Una de las cosas más importantes de entender en la trigonometría es que todas las funciones están interrelacionadas. Mientras que los valores de seno, coseno, tangente, etc., tienen todos sus usos propios, son más útiles por las relaciones que existen entre ellos. El radio modifica la escala de estas relaciones para que sean entendidas fácilmente. Una vez que entiendas el radio, puedes usar las relaciones que describe para mostrar otros problemas. ^{[4]
X
Fuente de investigación}

Anuncio

Método 2

Método 2 de 4:
Entender las aplicaciones de la trigonometría

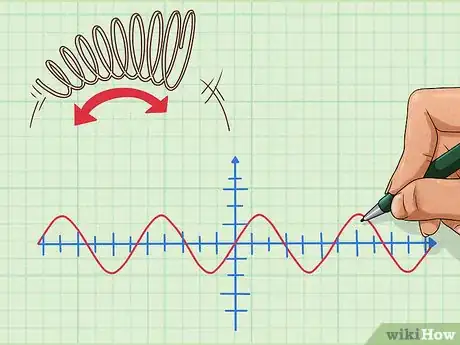
1
Comprende los usos básicos de la trigonometría en las universidades. Aparte de estudiar trigonometría solo por el amor a ella, los matemáticos y científicos aplican estos conceptos. La trigonometría se puede usar para encontrar los valores de ángulos o segmentos de línea. También puedes describir cualquier comportamiento cíclico graficándolo como función trigonométrica.^{[5]
X
Fuente de investigación}
- Por ejemplo, el movimiento de rebote de un resorte de ida y de vuelta se puede describir mediante la representación gráfica de una onda sinusoidal.
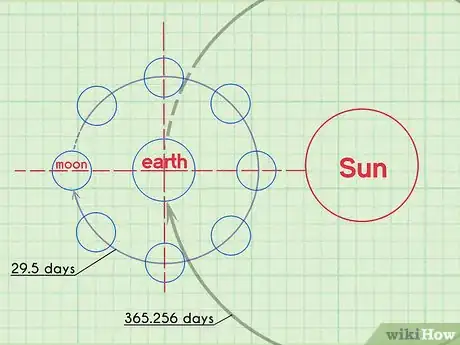
2
Piensa en los ciclos en la naturaleza. A veces, la gente lucha para comprender conceptos abstractos en matemáticas o en ciencias. Si te das cuenta de que esos conceptos están presentes en el mundo que te rodea, a menudo adquieren una luz nueva. Busca cosas en tu vida que ocurran en ciclos y trata de relacionarlas con la trigonometría.^{[6]
X
Fuente de investigación}
- La luna tiene un ciclo predecible que dura aproximadamente 29,5 días.
3
Visualiza cómo se podrían estudiar los ciclos naturales. Una vez que te des cuenta de que la naturaleza está llena de ciclos, comienza a pensar exactamente cómo los estudiarías. Piensa en cómo luciría un gráfico de tales ciclos. Partiendo del gráfico, podrías formular una ecuación para describir los fenómenos que observaste. Esto le dará sentido a las funciones trigonométricas para ayudarte a entender sus usos.^{[7]
X
Fuente de investigación}
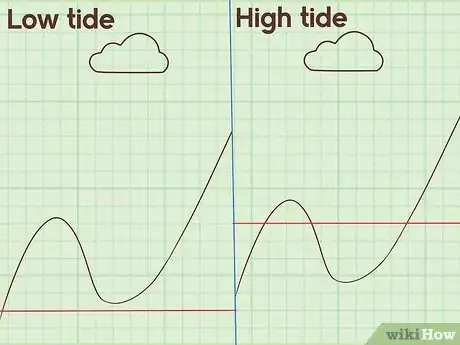
- Piensa en medir la marea de una cierta playa. Cuando la marea está alta se encuentra a cierta altura, y luego retrocede hasta que alcanza la marea baja. Desde la marea baja, el agua se mueve hasta la playa hasta que alcanza otra vez la marea alta. Este ciclo podría continuar indefinidamente, y se podría graficar como una función trigonométrica, como una ola coseno.
Anuncio

Método 3

Método 3 de 4:
Estudiar por adelantado

1
Lee el capítulo. Los conceptos trigonométricos a menudo son difíciles de comprender la primera vez para algunas personas. Si lees el capítulo antes de verlo en el salón de clases, estarás más familiarizado con el material. Mientras más veces lo veas, más conexiones harás de cómo se relacionan los conceptos diferentes en la trigonometría.^{[8]
X
Fuente de investigación}
- Esto también te permitirá identificar cualquier concepto que te cueste antes de la clase.
2
Mantén un cuaderno. Hojear un libro es mejor que nada, pero no es el tipo de lectura profunda que te ayudará a aprender trigonometría. Mantén notas detalladas del capítulo que leas. Recuerda que la trigonometría es acumulativa y que los conceptos se complementan entre ellos, así que tener notas de capítulos previos te puede ayudar a entender el capítulo actual.^{[9]
X
Fuente de investigación}
- También escribe cualquier pregunta que le quieras hacer al instructor.
3
Trabaja los problemas del libro. Algunas personas visualizan bien la trigonometría, pero también hay que realizar los problemas. Para asegurarte de que realmente entiendes el material, trata de resolver algunos problemas antes de la clase. De esta manera, si tienes dificultades, sabrás exactamente con qué necesitas ayuda en la clase.^{[10]
X
Fuente de investigación}
- La mayoría de los libros tienen las respuestas a algunos problemas en la parte de atrás. Esto te permite verificar tu trabajo.
4
Lleva los materiales a la clase. Llevar tus notas y los problemas de práctica a la clase te dará un punto de referencia. Esto refrescará las cosas que entiendes, y te recordará los conceptos en los que necesitas más explicación. Asegúrate de clarificar cualquier pregunta que hayas listado durante tu lectura.

Anuncio

Método 4

Método 4 de 4:
Tomar notas en clase

1
Escribe en el mismo cuaderno. Los conceptos trigonométricos están todos relacionados. Lo mejor es que practiques mantener todas tus notas en un lugar para que puedas volver a las notas anteriores. Designa un cuaderno específico o carpeta para el estudio trigonométrico.^{[11]
X
Fuente de investigación}
- También puedes seguir practicando problemas en este cuaderno.
2
Haz que la trigonometría sea una prioridad en clases. Evita usar el tiempo de clase para socializar o para hacer la tarea de otra clase. Cuando estés en la clase de trigonometría, debes estar concentrado en ella y en los problemas de práctica. Escribe cualquier nota que el instructor escriba en la pizarra o que indique que sea importante.
3
Sigue practicando en la clase. Ofrécete para resolver los problemas de la pizarra o comparte tus respuestas a un problema práctico. Haz preguntas si no entiendes algo. Mantén la comunicación tan abierta y fluida como lo permita el instructor. Esto facilitará aprender y disfrutar de la trigonometría.
- Si tu instructor prefiere dar la clase sin interrupciones, puedes guardar las preguntas para después de la clase. Recuerda que el trabajo del instructor es ayudarte a aprender trigonometría, así que no seas tímido.
4
Haz un seguimiento con más problemas de práctica. Completa cualquier tarea asignada. Los problemas de las tareas son buenos indicadores de las preguntas del examen. Asegúrate de entender cada uno. Si no te dan ninguna tarea, realiza problemas de tu libro que reflejen los conceptos cubiertos en la clase más reciente.^{[12]
X
Fuente de investigación}

Anuncio

Consejos

Recuerda que las matemáticas son una forma de pensar, no solo fórmulas para memorizar.
Revisa conceptos algebraicos y geométricos.

Anuncio

Advertencias

Estudiar de forma exagerada para un examen de trigonometría funciona raramente.
No aprenderás trigonometría a través de la memorización forzada. Tienes que entender los conceptos implicados.

Anuncio