Cet article a été coécrit par Marcus Raiyat. Marcus Raiyat est un opérateur de marché britannique, spécialiste des transactions sur les marchés financiers, fondateur et directeur général de Logikfx. Il possède près de 10 ans d'expérience, et connait très bien le négoce actif de devises (forex), d'actions et de cryptomonnaies. Il est spécialisé notamment dans le négoce des contrats pour différence (CFD), la gestion de portefeuille et l'analyse quantitative. Marcus est titulaire d'une licence en mathématiques de l'université d'Aston. Son travail chez Logikfx lui a permis d’être désigné en tant que « Best Forex Education & Training UK 2021 » par Global Banking and Finance Review.
Cet article a été consulté 65 778 fois.
Une obligation est une créance entrainant un paiement d'un montant d'intérêt fixe jusqu'à l'échéance. À la fin de l'échéance de l'obligation, le principal est remboursé au détenteur de l'obligation. Les investisseurs, la plupart du temps, cherchent à connaitre la valeur actuelle des obligations. La valeur actuelle, c'est-à-dire la valeur actuelle des flux futurs espérés, est utilisée pour mieux comprendre les différents facteurs qu'un investisseur peut considérer avant de prendre une décision d'investissement. Pour déterminer la valeur actuelle d'une obligation, vous devez effectuer deux calculs. Les investisseurs tiennent compte de la valeur actuelle des paiements d'intérêt et de la valeur actuelle du montant principal reçue à l'échéance.
Étapes
Partie 1
Partie 1 sur 2:Analyser les bases de l'obligation
-
1Comprenez le fonctionnement des obligations et le pourquoi elles sont émises. Une obligation est un instrument de dette. Les entités émettent des obligations pour collecter de l'argent pour un objectif spécifique. Les gouvernements, la plupart du temps, émettent des obligations pour réunir un capital afin de financer des projets publics tels que la construction des routes ou des ponts. Les entreprises émettent des obligations pour augmenter leur capital afin de développer leurs activités [1] .
- Toutes les informations sur l'obligation sont indiquées dans le contrat d'émission de l'obligation. Généralement, les obligations sont émises en multiples de 1 000 euros. Supposons, par exemple, que la société IBM émet une obligation de 1 000 000 d'euros à un taux de 6 % pendant 10 ans. La période considérée pour le paiement des intérêts est semestrielle.
- Les 1 000 000 d'euros représentent la valeur nominale ou le montant principal de l'obligation. Il s'agit du montant qui doit être remboursé par l'émetteur de l'obligation à l'investisseur, à l'échéance.
- IBM (l'émetteur) doit rembourser 1 000 000 d'euros aux investisseurs à la fin des 10 ans. L'échéance de l'obligation est de 10 ans.
- L'obligation génère un intérêt de 1 000 000 d'euros multipliés par 6 %, soit 60 000 euros par an. Puisque le paiement de l'intérêt est semestriel, l'émetteur doit effectuer deux paiements de 30 000 euros chacun.
-
2Sachez comment la détention d'une obligation peut être bénéfique pour un investisseur. Réutilisant le même exemple précédent, sachez qu'une douzaine d'investisseurs peuvent acheter chacun une portion de l'obligation de 1 000 000 d'euros. Chaque investisseur recevra deux paiements d'intérêt par an et recevra à l'échéance le montant principal investi ou la valeur nominale de l'obligation [2] .
- Les personnes retraitées ont tendance à acheter des obligations, à cause du flux de revenus prévisible des paiements d'intérêts.
- Toutes les obligations sont évaluées selon leurs capacités à payer les intérêts et à rembourser le principal à temps. Une obligation avec une bonne évaluation est considérée comme un investissement sécurisé à cause de la garantie qu'elle représente.
- Les obligations les bien moins évaluées appliquent généralement un taux d'intérêt plus élevé, car représentant un plus gros risque.
- Supposons que les sociétés IBM et Acme ont émis une obligation à échéance de 10 ans. IBM a une cote de crédit ou notation financière élevée et offre un taux d'intérêt de 6 %. Si Acme a une notation inférieure, elle devra offrir un taux d'intérêt supérieur à 6 % pour pouvoir attirer les investisseurs.
-
3Calculez la valeur actuelle. Pour calculer la valeur actuelle d'une obligation à n'importe quel moment de l'échéance, il suffit d'additionner la valeur actuelle des paiements d'intérêts à la valeur actuelle du principal que vous recevez à l'échéance [3] .
- La valeur actuelle ajuste la valeur d'un futur paiement au cours d'une devise. Disons par exemple que vous espériez recevoir 100 euros dans 5 ans. Pour savoir ce que le paiement de 100 euros vaut aujourd'hui, vous devez calculer la valeur actuelle des 100 euros.
- Le montant en euros est actualisé en utilisant un taux de rendement sur la période. Ce taux de rendement est souvent appelé taux d'actualisation.
- Un investisseur peut choisir un taux d'actualisation en utilisant diverses approches. Le taux d'actualisation peut être votre estimation du taux d'inflation sur l'échéance restante de l'obligation. Cela peut être aussi le taux de rendement minimum espéré. Le minimum espéré est basé sur l'évaluation du crédit de l'obligation et le taux d'intérêt appliqué sur les obligations de qualité similaire.
- Supposons que vous choisissez un taux d'actualisation de 4 % pour le paiement dû de 100 euros sur une période de 5 ans. Le taux d'actualisation est utilisé pour actualiser la valeur de vos futurs paiements par rapport au cours de l'euro. Dans ce cas, vous calculerez la valeur actuelle d'une seule somme d'argent.
- Vous trouverez sur le net des tableaux de valeur actuelle qui vous aideront à faire vos calculs ou vous pouvez utiliser une calculatrice de valeur actuelle en ligne. Si vous utilisez un tableau, vous trouverez le facteur de la valeur actuelle pour un taux d'actualisation de 4 % sur 5 ans. Ce facteur est 0,822. La valeur actuelle des 100 euros est 82,20 euros (100 euros x 0,822 = 82,20 euros).
- La valeur actuelle de votre obligation est : la valeur actuelle de tous les paiements d'intérêts + la valeur actuelle du montant principal remboursé à l'échéance.
Publicité
Partie 2
Partie 2 sur 2:Utiliser les formules de la valeur actuelle
-
1Utilisez le concept d'annuité pour calculer la valeur de vos paiements d'intérêts. Une annuité est un montant spécifique payé à un investisseur pour une période de temps donné. Les paiements d'intérêts sur votre obligation sont considérés comme un type d'annuité [4] .
- En calculant la valeur actuelle de vos paiements d'intérêts, vous calculez la valeur d'une série de paiements d'un montant fixe de chaque année sur toute l'échéance. Par exemple, si l'émetteur d'une obligation de 1 000 euros avec une échéance de 10 ans vous verse des intérêts à un taux de 10 % annuel, vous recevrez un montant fixe de 100 euros par an pendant 10 ans.
- La formule de calcul de la valeur actuelle nécessite que vous convertissiez les paiements d'intérêts annuels en paiements d'intérêts selon le nombre de paiements que vous recevez par an. Par exemple, supposons qu'avec votre obligation de 1 000 euros, vous recevez des paiements d'intérêts deux fois par an. Ceci dit, dans votre calcul, vous devez considérer deux paiements de 50 euros par an.
- Plus tôt, vous recevrez un paiement, plus c'est avantageux. Ce concept est parfois appelé la valeur temporelle de l'argent. Recevoir un euro aujourd'hui est sans doute plus avantageux que de recevoir un euro demain, car durant la période que vous détenez le 1 euro, vous pouvez l'investir (ou le dépenser) et obtenir un gain. Suivant cette logique, si vous recevez 50 euros en juin et 50 euros en décembre, ces paiements sont plus avantageux que de recevoir 100 euros en décembre, car vous avez la possibilité d'utiliser les 50 euros sans avoir à attendre la fin de l'année.
-
2Appliquez la formule de la valeur actuelle d'une annuité (VAA) aux paiements d'intérêts. La formule est . Les variables présentes dans la formule nécessitent que vous connaissiez le montant de paiement d'intérêt, le taux d'actualisation (ou taux de rendement requis) et le nombre d'années restant avant l'échéance [5] .
- Supposons qu'une obligation a une valeur nominale de 1 000 euros et un taux de coupon de 6 %. L'intérêt annuel est de 60 euros.
- Divisez le montant de l'intérêt annuel par la fréquence de paiement de l'intérêt par an. Ce calcul vous donnera I le montant de l'intérêt périodique payé. Par exemple, si l'obligation paie un intérêt semestriel, I = 30 euros par période. Chaque période est de 6 mois.
- Déterminez le taux d'actualisation. Divisez le taux d'actualisation requis par le nombre de périodes dans l'année pour déterminer le taux de rendement requis par période qui est k. Par exemple, pour un taux de rendement annuel requis de 5 % pour une obligation payant des intérêts semestriels, k = (5 %/2) = 2,5 %.
- Calculez la fréquence de paiement de l'intérêt sur la durée de vie de l'obligation ou encore la variable n. Multipliez le nombre d'années composant l'échéance par la fréquence de paiement de l'intérêt dans l'année. Exemple : supposons que l'échéance de l'obligation est de 10 ans et que le paiement d'intérêt est semestriel. Dans ce cas, n = (10 x 2) = 20 paiements d'intérêts.
- Remplacez I, k et n dans la formule de la valeur actuelle de l'annuité pour déterminer la valeur actuelle des paiements d'intérêts. Dans cet exemple, la valeur actuelle des paiements d'intérêts est 30 euros[1-(1+0,025)^-20]/0,025 = 467,67 euros.
-
3Entrez les variables et calculez la valeur actuelle des paiements du principal. La valeur actuelle des paiements d'intérêts est une annuité ou une chaine de paiements. Le remboursement du principal se fait en un seul versement à l'investisseur, à l'échéance [6] .
- Si, par exemple, vous détenez une obligation de 100 000 euros avec une échéance de 10 ans, l'obligation a probablement une valeur nominale de 1 000 euros. 100 000 euros représentent le principal. Vous recevrez un paiement unique de 100 000 euros après 10 ans. Vous utiliserez un taux d'actualisation pour actualiser ce paiement unique en une valeur actuelle.
- La formule utilise certaines des mêmes valeurs que vous avez utilisées dans la formule de l'annuité. Utilisez premièrement la formule de l'annuité puis appliquez ces mêmes variables à la formule du paiement du principal.
- Insérez k et n dans la formule de la valeur actuelle. Utilisez la formule Valeur actuelle = Valeur nominale/(1+k)^n pour déterminer la valeur actuelle du principal à l'échéance. Dans le cas de notre exemple, valeur actuelle = 1 000 euros/(1+0,025)^10 = 781,20 euros.
- Additionnez la valeur actuelle de l'intérêt à la valeur actuelle du principal pour trouver la valeur actuelle de l'obligation. Dans le cas de notre exemple, valeur de l'obligation = (467,67 euros + 781,20 euros) ou 1 248,87 euros.
- Les investisseurs utilisent la valeur actuelle pour décider si cela vaut la peine d'investir dans une obligation spécifique.
Publicité
Références
- ↑ http://www.getrichslowly.org/blog/2009/04/21/investing-101-how-bonds-work/
- ↑ http://www.kiplinger.com/article/investing/T052-C000-S001-how-bonds-work.html
- ↑ http://www.investopedia.com/terms/p/presentvalue.asp
- ↑ http://www.investorwords.com/225/annuity.html
- ↑ http://www.investopedia.com/articles/03/101503.asp
- ↑ http://www.accountingcoach.com/bonds-payable/explanation



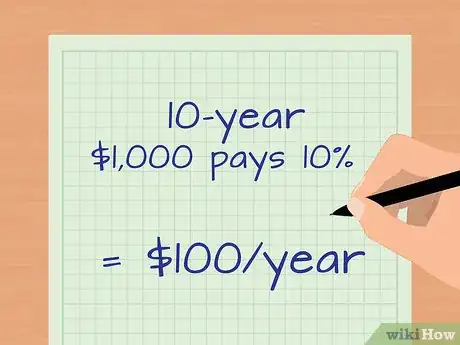
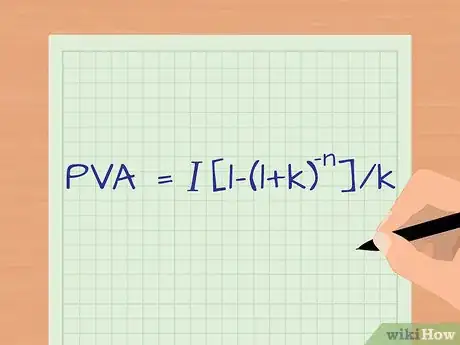
![VAA=I[1-(1+k)^{-}n]/k](./images/2013929532-d7271cdf7429766bbe54abcf28d40dbde2b5228f.webp)



-Step-20-Version-5.webp)