Comment calculer la vitesse moyenne

Pour calculer une vélocité moyenne, il vous faut un objet (voiture, piéton, particule) en déplacement, mais cela ne suffit pas. En plus de la vitesse de cet objet, vous devez préciser la direction (avant, arrière, sud, nord…) du déplacement dans l'espace. Pour compliquer un peu la chose, l'objet peut subir des changements de direction et de vitesse, mais rassurez-vous, il y a des formules.

Partie 1

Partie 1 sur 2:
Calculer une vélocité moyenne (sans accélération)

1
Sachez que la vélocité comprend une vitesse et une direction. Cette notion physique mesure la variation de vitesse d'un objet qui se déplace ^{[1]
X
Source de recherche}. Dans cette notion bien particulière, il y a une notion de vitesse (par exemple, 100 m/s), mais aussi de direction (par exemple, vers le sud). En conséquence, une vélocité de 100 m/s vers le sud et une autre de 100 m/s vers le nord semblent identiques, mais il n'en est rien à cause de la direction.
- La vélocité, aussi appelée vecteur vitesse, a un sens bien précis en physique ^{[2]
  X
  Source de recherche}. Pour distinguer un vecteur d'une quantité scalaire ou non orientée, on trace au-dessus du symbole une flèche. Là où $v$ représente la vitesse, ${\vec {v}}$ représente le vecteur vitesse (ou vélocité) ^{[3]
  X
  Source de recherche}. Dans l'article, nous n'utiliserons pas la notation vectorielle, mais le module ( $v$ ) du vecteur en ajoutant la direction.
- Dans des exercices académiques, le module d'une vélocité s'exprime en mètres par seconde (m/s), mais une autre unité est possible (km/h).
2
Calculez le déplacement apparent. Le déplacement est la variation de position d'un objet, qui tient compte, entre les points de départ et d'arrivée, à la fois de la distance parcourue et de la direction ^{[4]
X
Source de recherche}. Avec la vélocité, peu importe, les changements de direction, seule compte la distance entre les points de départ et d'arrivée. Nous prendrons ici des exemples d'objets se déplaçant à vitesse constante dans une seule direction.
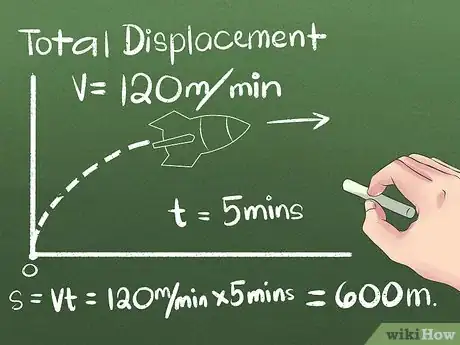
- Imaginons une fusée se dirigeant pendant 5 minutes vers le nord à une vitesse constante de 120 mètres à la minute. La fusée parcourra 600 m vers le nord
  (5 x 120).La formule mathématique est la suivante : $d=vt$ , avec $d$ la distance parcourue, $v$ , la vitesse de l'objet et $t$ le temps de parcours.
- Si l'objet avait une vitesse qui s'accélérait de façon constante, la formule serait :
  $d=vt+{\frac {at^{2}}{2}}$ , $a$ étant l'accélération. Ce sera l'objet de la seconde partie.
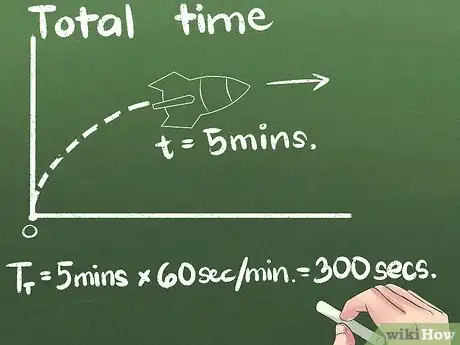
3
Déterminez le temps de parcours. La vélocité moyenne peut s'exprimer avec n'importe quelle unité de temps, mais la seconde reste l'unité du Système international d'unités (SI). Pour convertir 5 minutes (vol de la fusée) en secondes, il suffit de multiplier par 60 : (5 minutes) x (60 secondes/minute) = 300 secondes.
- Si l'unité de temps était en heures ou en jours, il serait plus simple de calculer la vélocité avec cette unité et de convertir le résultat en mètres par seconde (m/s).
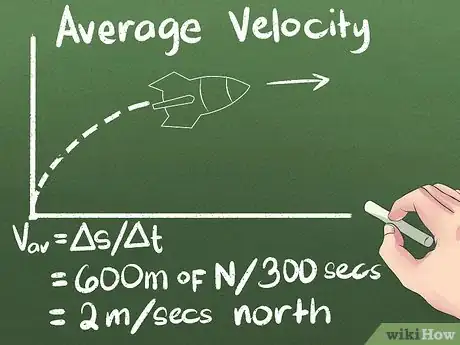
4
Pensez la vélocité moyenne comme un rapport. C'est celui d'une distance parcourue en un temps donné. Si vous avez ces deux informations, alors vous pouvez calculer une vélocité ^{[5]
X
Source de recherche}. Une fusée qui parcourt 600 mètres vers le nord en 300 secondes a une vélocité de : 600 m / 300 s = 2 m/s vers le nord.
- N'oubliez pas d'indiquer la direction (ici vers le nord, dans un autre exemple, ce pourra être vers l'arrière).
- La formule de la vélocité moyenne est la suivante : ${\vec {v_{m}}}={\frac {\Delta d}{\Delta t}}$ . Dans cette expression littérale, $\Delta$ symbolise toujours une variation, si bien que le rapport ${\frac {\Delta d}{\Delta t}}$ peut se traduire par la variation de position ( $d$ ) durant une période de temps.
- La vélocité moyenne s'écrit ainsi : ${\vec {v}}$ , étant entendu que l'objet se déplace dans un repère.
5
Résolvez des problèmes de vitesse plus difficiles. Avec des objets ayant des vitesses ou des directions variables, la résolution est un peu plus complexe. La formule de la vélocité moyenne est toujours la même : le rapport du déplacement direct entre deux points sur le temps mis, augmenté d'une direction. Peu importe ce qui se passe entre le point de départ et celui d'arrivée : changement de direction ou de vitesse. Rien ne vaut des exemples pour le prouver.
- Anna marche vers l'ouest pendant 2 secondes à une vitesse de 1 m/s, puis continue dans cette même direction pendant encore 2 secondes, mais à une vitesse de 3 m/s. Elle aura donc parcouru : (1 m/s)(2 s) + (3 m/s)(2 s) vers l'ouest, soit 8 mètres. Son déplacement aura duré 4 secondes (2 + 2). Sa vélocité moyenne a été la suivante : 8 m / 4 s, soit 2 m/s vers l'ouest.
- Pierre marche vers l'ouest pendant 3 secondes à une vitesse de 5 m/s, puis fait demi-tour pendant 1 seconde vers l'est à une vitesse de 7 m/s. Ce dernier déplacement sera négatif par rapport au déplacement vers l'ouest. Le déplacement apparent est le suivant : (5 m/s ouest)(3 s) + (-7 m/s ouest)(1 s) = 15 m - 7 m, soit 8 mètres. Son déplacement aura duré 4 secondes et sa vélocité moyenne aura été de : 8 m ouest / 4s, soit 2 m/s vers l'ouest.
- Charlotte marche 1 mètre vers le nord, puis 8 vers l'ouest et enfin, 1 vers le sud. Elle a marché pendant 4 secondes au total. Tracez son itinéraire et vous vous apercevrez que le point d'arrivée est à 8 mètres à l'ouest du point de départ. Le temps de déplacement est encore de 4 secondes, ce qui fait que la vélocité moyenne est aussi de : 8 m ouest / 4s = 2 m/s vers l'ouest.
Publicité

Partie 2

Partie 2 sur 2:
Calculer une vélocité moyenne (avec accélération)

1
Inscrivez la vélocité initiale et l'accélération. Prenons l'exemple d'un vélo qui se déplacerait vers la droite à une vitesse initiale de 5 m/s, et accélèrerait à une vitesse constante de $2\ m/s^{2}$ $2\ m/s^{2}$ . Au bout de 5 secondes, quelle sera la vitesse du vélo ?
- Si m/s² ne vous parle pas, vous pouvez l'écrire m/(s x s) ou m.s^-2, qui se lit : mètres par seconde au carré ^{[6]
  X
  Source de recherche}. Une accélération de 2 m/s² se traduit par une vitesse qui augmente, chaque seconde, de 2 m/s.
2
Utilisez l'accélération pour trouver la vélocité finale. L'accélération ( $a$ $a$ ) est la variation du vecteur vitesse ^{[7]
X
Source de recherche}. Pour simplifier, nous n'évoquerons ici que le cas d'une accélération constante. Partant de cette hypothèse, il est facile de dresser un tableau des vitesses à des temps t successifs. Dans notre exemple, l'accélération dure 5 secondes, il est facile de trouver les vitesses à chaque seconde.
- À t = 0 (début de l'expérience), le vélo roule tout droit à une vitesse de 5 m/s.
- À t = 1, le vélo roule à une vitesse de : 5 m/s + at, soit 5 m/s + (2 m/s²)(1 s), c'est-à-dire 7 m/s.
- À t = 2, le vélo roule à une vitesse de : 5+(2)(2) = 9 m/s.
- À t = 3, le vélo roule à une vitesse de : 5+(2)(3) = 11 m/s.
- À t = 4, le vélo roule à une vitesse de : 5+(2)(4) = 13 m/s.
- À t = 5, le vélo roule à une vitesse de : 5+(2)(5) = 15 m/s.
3
Utilisez la formule de calcul de la vélocité moyenne. La vélocité moyenne
( $v_{m}$ $v_{m}$ ) sur un parcours donné est égale à la moyenne de la vitesse initiale ( $v_{i}$ $v_{i}$ ) et de la vitesse finale ( $v_{f}$ $v_{f}$ ) si et seulement si l'accélération est constante :
$v_{m}={\frac {v_{f}+v_{i}}{2}}$ $v_{m}={\frac {v_{f}+v_{i}}{2}}$ . Ici, la vitesse initiale ( $v_{i}$ $v_{i}$ ) du vélo est de 5 m/s. En bout de parcours, sa vitesse ( $v_{f}$ $v_{f}$ ) est de 15 m/s. Vous allez trouver que la vélocité moyenne est de 10 m/s vers la droite : (15 + 5)/2 = 10.
- Nous avons travaillé sur la vitesse qui se transforme en vélocité dès lors que nous précisons, la direction (vers la droite).
- La vitesse initiale sera notée $v_{i}$ (ou $v_{0}$ au temps t = 0) et $v_{f}$ sera la vitesse en fin d'accélération.
4
Comprenez intuitivement ce que la vélocité moyenne. Si c'était possible, pour trouver la vraie vélocité moyenne d'un objet en déplacement, il faudrait prendre la vélocité à tous les instants et en faire la moyenne. Comme le temps est fractionnable à l'infini, le calcul serait quasi impossible à moins d'en passer par le calcul infinitésimal. Sans recourir à ces calculs complexes, vous imaginez bien que la vitesse moyenne entre les deux premières secondes du parcours est inférieure à la vitesse moyenne entre les deux dernières secondes, car il y a eu entre temps accélération.
5
Vérifiez ce calcul de façon intuitive. La vélocité moyenne sur l'ensemble d'un parcours peut être retrouvée en faisant la moyenne des deux vélocités qui sont à égale distance de la moitié du temps. Ici, c'est le cas avec t = 0 et t = 5, ou t = 1 et t = 4, ou encore t = 2 et t = 3. Cela marche aussi avec des temps non entiers (t = 1,5 et t = 3,5).
- Quelle que soit la paire de points prise, à condition que les temps soient symétriques, vous tomberez toujours sur la vélocité moyenne globale. Dans notre exemple : (5+15)/2 = (7+13)/2 = (9+11)/2 = 10 m/s… vers la droite.
6
Terminez le raisonnement par intuition. De ce qui précède, c'est-à-dire une sorte de raisonnement par récurrence, vous pouvez en tirer la conclusion que la moyenne de la vélocité d'un objet sur un parcours donné peut s'obtenir avec deux seules vélocités prises à deux instants t, lesquels seront à égale durée de temps du milieu du temps de parcours.
- Les moyennes obtenues avec les paires symétriques se résument à une seule, il est donc inutile de les calculer toutes, à condition que l'accélération soit constante. Dans l'exemple, on a trouvé plusieurs fois 10 m/s vers la droite, c'est donc la vélocité moyenne sur l'ensemble du déplacement.
- Le plus simple, et c'est ce que l'on fait généralement, est de calculer la moyenne des vélocités de départ et d'arrivée. Dans notre exemple, avec t = 0 et t = 5, l'application de la formule donne l'égalité suivante : (5 m/s +15 m/s)/2 = 10 m/s vers la droite.
7
Comprenez la formule mathématique de la vélocité moyenne. L'intuition est certes commode, mais il faut la rendre sous forme d'équation. Nous ne prendrons que les quantités scalaires des données, en gardant en tête la direction ^{[8]
X
Source de recherche}.
- $d=v_{i}t+{\frac {at^{2}}{2}}$ (l'écriture est simplifiée : la distance $d$ est en fait $\Delta d$ , la variation de position, et $t$ est $\Delta t$ , la variation de position).
- La vélocité moyenne ( $v_{m}$ ) étant égale à ${\frac {d}{t}}$ , il est possible de faire le remplacement de $d$ :
- $v_{m}={\frac {d}{t}}=v_{i}+{\frac {at}{2}}$ .
- Le produit de l'accélération par le temps ( $at$ ) vous donne la variation de vitesse, soit $v_{f}-v_{i}$ . On remplacera donc $at$ par cette dernière différence :
- $v_{m}=v_{i}+{\frac {v_{f}-v_{i}}{2}}$ .
- Simplifiez : $v_{m}=v_{i}+{\frac {v_{f}}{2}}-{\frac {v_{i}}{2}}={\frac {v_{i}}{2}}+{\frac {v_{f}}{2}}={\frac {v_{f}+v_{i}}{2}}$ .
Publicité

Conseils

La vélocité se différencie de la vitesse en ce que la première est une quantité vectorielle, tandis que la seconde est une quantité scalaire. Un vecteur a une direction, un sens et une norme (ou module), un scalaire n'est défini que par sa norme.
Quand un objet se déplace dans un espace à une dimension, sur une ligne donc, conventionnellement il a été posé que les déplacements vers la droite étaient positifs et ceux vers la gauche négatifs. Notez-le quelque part en début d'exercice.
Pour calculer la vitesse d'un objet à un temps t particulier, vous devez calculer non pas sa vitesse moyenne, ce qui n'aurait aucun sens, mais sa vitesse-instantanée.