Comment calculer des volumes

Le mètre cube (m³) est une unité de volume dérivée du mètre, une des unités de base du Système international d’unités (SI). Tout volume avec une autre unité peut être convertie en m³, moyennant un facteur de conversion précis. Et pour donner un côté concret au propos, les cas du volume d'un prisme rectangulaire et d'un cylindre seront exposés, ils ont en effet en commun d'avoir la même formule : leurs volumes sont le produit de la base par la hauteur. Entre les deux, seul change le calcul de l'aire de base.

Méthode 1

Méthode 1 sur 3:
Convertir en mètres cubes

1
Divisez par 1 000 000 pour convertir des cm³ en m³. Avec les volumes, le rapport de puissance est un multiple de 3 : 1 m³ équivaut à 1 000 000 cm³, ce qui fait qu'à l'inverse, il faut diviser le nombre de cm³ par 1 000 000 pour obtenir des m³. La conversion dans ce sens est peu fréquente, mais cela peut arriver dans un exercice scolaire ^{[1]
X
Source de recherche}.
- Pour convertir 3 896 547 cm³ en m³, divisez par 1 000 000. Cette division est facile, il faut déplacer la virgule : 3 896 547 cm³ = 3,896 547 m³.
2
Multipliez par 1 000 000 000 pour convertir des km³ en m³. Le kilomètre est un multiple du mètre dans un rapport de 1000:1, si bien que les kilomètres cubes sont aussi un multiple des m³ dans un rapport de 1 000 000 000:1. Un kilomètre cube équivaut à un milliard de m³ ^{[2]
X
Source de recherche} !
- Pour calculer la pression atmosphérique, l'on vous donne une tranche d'air de 1,21 km³ (cube de 1,1 km), soit 1 210 000 000 m³.
3
Divisez par 1 000 pour convertir des litres en mètres cubes. Le litre est une unité de volume qui, dans la vie courante, est aussi fréquemment utilisée que le m³. Il suffit de retenir qu'il y a 1 000 litres dans un m³ pour faire les conversions. Pour convertir des litres en m³, il faut diviser par 1 000 ^{[3]
X
Source de recherche}.
- Si vous avez une citerne de fioul qui peut contenir 3 500 litres, alors vous pourrez aussi dire qu'elle contient 3,5 m³ (3 500/1 000). Sur la facture, il y a souvent les 2 unités.
4
Multipliez par 0,8 pour convertir des stères en mètres cubes. Le stère est l'unité du bois de chauffe. En théorie, un stère équivaut à 1 m³, mais comme le bois coupé laisse des espaces, 1 stère correspond à un volume entre 0,7 et 0,85 m³ ^{[4]
X
Source de recherche}.
- Soit un stère de bois contenant 0,80 m³ (buches de 55 cm), si vous en achetez 5, vous allez pouvoir réellement bruler 4 m³ de bois.
Publicité

Méthode 2

Méthode 2 sur 3:
Calculer le volume d'un prisme rectangulaire

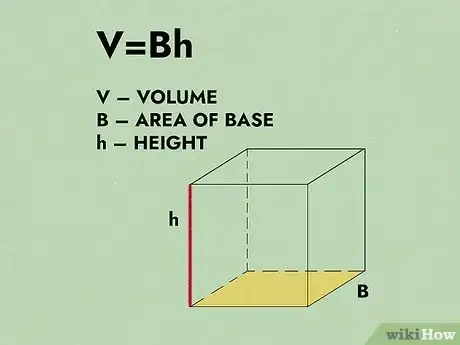
1
Retenez la formule ce calcul d'un prisme rectangulaire. Par prisme rectangulaire, on entend tout un solide limité par six rectangles. Si ces faces sont carrées, c'est un cube. La formule du volume d'un tel solide est la suivante : $V=Bh$ $V=Bh$ , $V$ $V$ étant le volume du prisme, $B$ $B$ l'aire de sa base et $h$ $h$ sa hauteur ^{[5]
X
Source de recherche}.
- Pour le calcul du volume, vous devez avoir des dimensions exprimées dans la même unité de longueur. Vous pourrez éventuellement convertir le volume en une autre unité plus adaptée.
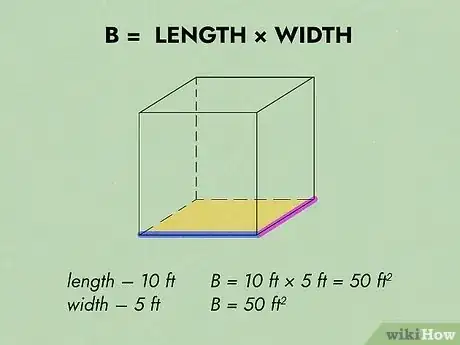
2
Calculez l'aire de la base du prisme. Elle s'obtient en multipliant sa longueur ( $L$ $L$ ) par sa largeur ( $l$ $l$ ). Là, de deux choses l'une : ou l'on vous donne ces dimensions ou vous les mesurez sur le croquis. Cela fait, multipliez ces 2 mesures. Faites attention à l'unité, elle doit être identique ^{[6]
X
Source de recherche}.
- Supposons que vous ayez le plan d'une de vos chambres qui fait 10 m de long sur 5 de large, vous obtenez une surface au sol de 50 m² (10 x 5).
- Comme vous le remarquez, non seulement vous multipliez les valeurs numériques, mais aussi les unités ( $m\times m=m^{2}$ ).
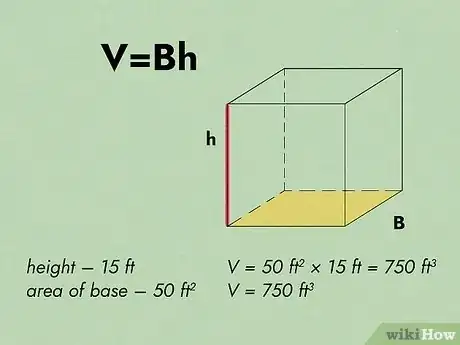
3
Multipliez l'aire de la base par la hauteur du prisme. Comme précédemment, ou l'on vous donne la hauteur ou vous la mesurez en vrai ou sur un schéma. L'unité sera la même que celle des 2 autres. Faites le produit de l'aire de la base ( $A_{p}$ $A_{p}$ ) par cette hauteur ^{[7]
X
Source de recherche}.
- Revenons à votre chambre : la hauteur sous plafond (c'est-à-dire la distance du sol au plafond) est de 3 m, le volume de la pièce est donc de 150 m³ (50 x 3).
Publicité

Méthode 3

Méthode 3 sur 3:
Calculer le volume d'un cylindre

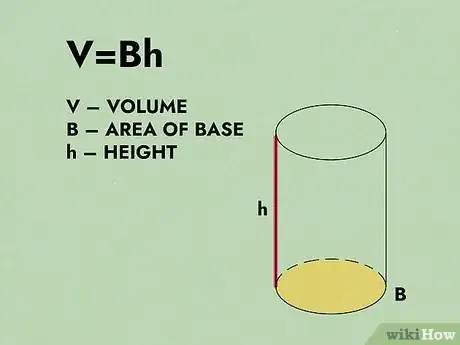
1
Utilisez la formule de calcul du cylindre. Elle est finalement assez simple : $V=Bh$ $V=Bh$ , formule dans laquelle $V$ $V$ est le volume du cylindre, $B$ $B$ l'aire de sa base et $h$ $h$ sa hauteur. Connaissant ces deux dernières valeurs, il suffit de les multiplier pour obtenir votre volume ^{[8]
X
Source de recherche}.
- Pour un résultat directement en m³, les deux valeurs doivent être respectivement en m² ( $B$ ) et en mètres ( $h$ ). Sinon il est possible de convertir au dernier moment si vos valeurs sont dans une autre unité.
2
Calculez l'aire de la base ( $A_{B}$ ) du cylindre. Par définition, c'est celle d'un cercle et la formule est la suivante : $A_{B}=\pi r^{2}$ $A_{B}=\pi r^{2}$ , avec $r$ $r$ le rayon du cercle et $\pi$ $\pi$ la constante bien connue. Là, de deux choses l'une : ou l'on vous donne ces dimensions ou vous les mesurez sur le croquis ou sur le terrain (trou d'un poteau cylindrique). Pour l'aire du cercle, il faut multiplier le rayon par lui-même, puis par $\pi$ $\pi$ (soit 3,14 ^{[9]
X
Source de recherche}).
- Au bas d'une descente d'eau pluviale, vous creusez un trou circulaire de 0,5 m pour faire un bassin de récupération des eaux de pluie. La surface au sol de votre conteneur sera de 0,25 m² (0,5 x 0,5). Ensuite, il ne reste plus qu'à multiplier par π (nous prendrons sa valeur de 3,14), ce qui donne :
  $A_{B}=0,785\ m^{2}$ .
- Pour le cercle comme pour toutes les autres figures, une aire s'obtient en multipliant deux dimensions qui dans le cas présent résument à une seule : le rayon.
- Si vous avez non pas le rayon, mais le diamètre du cercle, il vous suffira de le diviser par 2 pour retomber sur le rayon ( $D=2r$ ). Un cercle de 1 m de diamètre a un rayon de 0,5 m.
3
Calculez le volume du cylindre. Le plus compliqué est fait, puisqu'ayant l'aire de la base, il ne vous reste qu'à récupérer la hauteur (donnée, ou mesurée sur le croquis ou sur le terrain) de votre cylindre et à multiplier les deux ^{[10]
X
Source de recherche}.
- Reprenons l'exemple du bac des eaux pluviales. La base mesurait donc 0,785 m² et vous avez prévu de creuser sur 2 m de profondeur. Il vous faudra donc dégager un volume de terre de 1,57 m³ (0,785 x 2).
Publicité