ديناميكا جزيئية

الديناميكا الجزيئية (بالإنجليزية: Molecular dynamics (MD))، هي علم قائم على محاكاة حاسوبية للجزيئات والمركبات معتمدة على قوانين نيوتن للحركة في توقع حركة الجزيئات وسرعة تحركها واماكن وجودها بعد فترات زمنية قصيره جدا وهو عمل يتطلب حلول لمعادلات نيوتن لاعداد هائلة من الجزيئات ولفترات زمنية قصيره جدا ولضمان حساب هذه التوقعات بشكل صحيح أو اقرب للصحة يجب أخذ عدة امور عند حساب قوانين نيوتن مثل قوى التجاذب بين الجزيئات واهتزاز روابط الجزي وانثناء الرووابط حول محورها وتذبذب الزاوية بين ذرات الجزي وايضا تذبذب الزوايا بين مستويات الجزئ أو ما يعرف بالزاوية الزوجية وامور أخرى كثيرة

مثال على محاكاة ديناميات الجزيئية في نظام بسيط: ترسب أحد النحاس (النحاس) ذرة في البلورة الباردة من النحاس (مؤشر ميلر (001) سطح). تمثل كل دائرة موضع ذرة واحدة. يتم إعادة توزيع الطاقة الحركية للذرة التي تقترب من القمة بين الذرات الأخرى، لذلك بدلاً من الارتداد، تظل مرتبطة بسبب قوى الجذب بين الذرات.

غالبًا ما تُستخدم محاكاة الديناميكيات الجزيئية لدراسة الأنظمة الفيزيائية الحيوية. يصور هنا محاكاة 100 ps للماء.

وصف مبسط لخوارزمية محاكاة الديناميكيات الجزيئية القياسية، عند استخدام عامل تكامل من النوع المصحح والمتنبئ. قد تأتي القوى إما من الجهود الكلاسيكية بين الذرات (الموصوفة رياضياً كـ

F=-\nabla V({\vec {r}})

) أو ميكانيكي الكم (الموصوف رياضيًا كـ

F=F(\Psi ({\vec {r}}))

) طرق. توجد اختلافات كبيرة بين شركات التكامل المختلفة؛ لا يحتوي البعض على نفس المصطلحات ذات الترتيب الأعلى تمامًا كما هو موضح في مخطط التدفق، ويستخدم الكثير أيضًا مشتقات زمنية ذات ترتيب أعلى، ويستخدم البعض كلاً من الخطوة الزمنية الحالية والسابقة في مخططات الخطوات ذات الوقت المتغير.

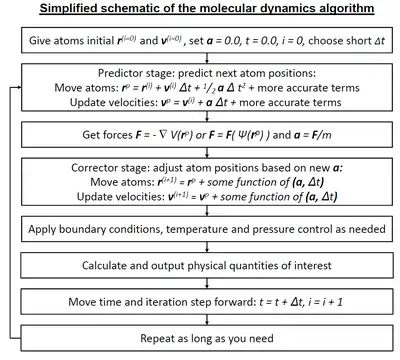
ولاننا في هذه العملية نقوب بحساب قوانين نيوتن وقوانين أخرى تتعلق بالمحاكاة لاعداد كبيرة جده من الجزيئات هذا يجعل العملية معقدة جدا وشبه مستحيلة لذلك يتم الاستعانة ببعض الفرضيات وطرق احصائية لتساعدنا في جعل هذه الحسابات ممكنة من الناحية العملية.[1][2][3]

الديناميكات الجزيئية هي طريقة محاكاة حاسوبية لتحليل الحركات الفيزيائية للذرات والجزيئات. يُسمح للذرات والجزيئات بالتفاعل لفترة زمنية محددة، مما يعطي نظرة على "التطور" الديناميكي للنظام. في الإصدار الأكثر شيوعًا، يتم تحديد مسارات الذرات والجزيئات عن طريق الحل العددي لمعادلات نيوتن للحركة لنظام من الجسيمات المتفاعلة، حيث تُحسب القوى بين الجسيمات وطاقاتها الكامنة غالبًا باستخدام الكمون بين الذرات أو مجالات القوة الجزيئية. يتم تطبيق الطريقة في الغالب في الفيزياء الكيميائية وعلوم المواد والفيزياء الحيوية.

نظرًا لأن الأنظمة الجزيئية تتكون عادةً من عدد كبير من الجسيمات، فمن المستحيل تحديد خصائص هذه الأنظمة المعقدة بشكل تحليلي؛ تتغلب محاكاة الديناميكا الجزيئية على هذه المشكلة باستخدام الطرق العددية. ومع ذلك، فإن عمليات محاكاة الديناميكا الجزيئية الطويلة غير مشروطة رياضيًا، مما يؤدي إلى حدوث أخطاء تراكمية في التكامل العددي يمكن تقليلها من خلال الاختيار المناسب للخوارزميات والمعلمات، ولكن لا يتم التخلص منها تمامًا.

بالنسبة للأنظمة التي تتبع فرضية إرغوديك، يمكن استخدام تطور محاكاة ديناميكية جزيئية واحدة لتحديد الخصائص الديناميكية الحرارية العيانية للنظام: المتوسطات الزمنية لنظام ergodic تتوافق مع متوسطات المجموعة الدقيقة. كما أطلق على الديناميكا الجزيئية أيضًا اسم "الميكانيكا الإحصائية بالأرقام" و "رؤية لابلاس للميكانيكا النيوتونية " للتنبؤ بالمستقبل من خلال تحريك قوى الطبيعة [4] والسماح بإلقاء نظرة ثاقبة على الحركة الجزيئية على نطاق ذري.

تاريخ

تم تطوير الديناميكا الجزيئية في الأصل في أوائل الخمسينيات من القرن الماضي، بعد النجاحات السابقة في محاكاة مونت كارلو، والتي يعود تاريخها إلى القرن الثامن عشر، في مشكلة إبرة بوفون على سبيل المثال، ولكن تم نشرها في الميكانيكا الإحصائية في مختبر لوس ألاموس الوطني بواسطة روزنبلوث ومتروبوليس فيما يعرف اليوم بخوارزمية متروبوليس-هاستينغز. يعود الاهتمام بالتطور الزمني لأنظمة الجسم N إلى القرن السابع عشر، بدءًا من نيوتن، واستمر في القرن التالي إلى حد كبير مع التركيز على الميكانيكا السماوية وقضايا مثل استقرار النظام الشمسي. تم تطوير العديد من الأساليب العددية المستخدمة اليوم خلال هذه الفترة الزمنية، والتي سبقت استخدام أجهزة الكمبيوتر؛ على سبيل المثال، خوارزمية التكامل الأكثر شيوعًا المستخدمة اليوم، خوارزمية تكامل فيرليت، تم استخدامها في وقت مبكر من عام 1791 بواسطة جان باتيست جوزيف ديلامبر. يمكن اعتبار الحسابات العددية باستخدام هذه الخوارزميات الديناميكا الجزيئية "يدويًا".

في وقت مبكر من عام 1941، تم تنفيذ تكامل معادلات الحركة للعديد من الأجسام مع أجهزة الكمبيوتر التناظرية. قام البعض بعمل كثيف العمالة لنمذجة الحركة الذرية من خلال بناء نماذج فيزيائية، على سبيل المثال، باستخدام المجالات العيانية. كان الهدف هو ترتيبها بطريقة تماثل بنية السائل واستخدامه لفحص سلوكه. برنال قال في عام 1962: " . . . أخذت عددًا من الكرات المطاطية وغرستهم معًا بقضبان بأطوال مختلفة تتراوح من 2.75 إلى 4 بوصات. حاولت القيام بذلك في المقام الأول بشكل عرضي قدر الإمكان، حيث أعمل في مكتبي الخاص، وأتعرض للمقاطعة كل خمس دقائق أو نحو ذلك ولا أتذكر ما فعلته قبل المقاطعة. " [5]

بعد اكتشاف الجسيمات المجهرية وتطوير أجهزة الكمبيوتر، توسع الاهتمام إلى ما وراء إثبات أنظمة الجاذبية إلى الخصائص الإحصائية للمادة. في محاولة لفهم أصل اللارجعة، اقترح فيرمي في عام 1953، ونشر في عام 1955، [6] استخدام مانياك، أيضًا في مختبر لوس ألاموس الوطني، لحل التطور الزمني لمعادلات الحركة للعديد من: يخضع نظام الجسم للعديد من خيارات قوانين القوة؛ اليوم، يُعرف هذا العمل الأساسي بمشكلة فيرمي - باستا - أولام - تسينغو. يظهر التطور الزمني للطاقة من العمل الأصلي في الشكل إلى اليمين.

تم إجراء واحدة من أولى عمليات المحاكاة لنظام N-body على MANIAC-I بواسطة Fermi وزملاؤه لفهم أصول اللارجعة في الطبيعة. الموضح هنا هو الطاقة مقابل الوقت لنظام 64 جسيمًا.

في عام 1957، استخدم بيرني ألدر ووينرايت [7] حاسوب آي بي إم 704 لمحاكاة التصادمات المرنة تمامًا بين المجالات الصلبة.[7] في عام 1960، ربما في أول محاكاة واقعية للمادة، جيبسون وآخرون. محاكاة التلف الإشعاعي للنحاس الصلب باستخدام نوع ولد ماير من التفاعل البغيض مع قوة سطحية متماسكة.[8] في عام 1964، نشر عبد الرحمن [9] محاكاة للأرجون السائل تستخدم كمون لينارد جونز. مقارنة حسابات خصائص النظام، مثل معامل الانتشار الذاتي، بشكل جيد مع البيانات التجريبية.[9]

مجالات التطبيق وحدودها

تم استخدام طريقة الديناميكا الجزيئية لأول مرة في الفيزياء النظرية، وقد اكتسبت شعبية في علم المواد بعد ذلك بوقت قصير، ومنذ السبعينيات أصبحت شائعة أيضًا في الكيمياء الحيوية والفيزياء الحيوية. يستخدم الديناميكا الجزيئية بشكل متكرر لتحسين الهياكل ثلاثية الأبعاد للبروتينات والجزيئات الكبيرة الأخرى بناءً على القيود التجريبية من علم البلورات بالأشعة السينية أو التحليل الطيفي بالرنين المغناطيسي النووي. في الفيزياء، يتم استخدام الديناميكا الجزيئية لفحص ديناميكيات الظواهر على المستوى الذري التي لا يمكن ملاحظتها مباشرة، مثل نمو الأغشية الرقيقة وزرع الأيونات الفرعية، وكذلك لفحص الخصائص الفيزيائية للأجهزة النانوية التي لم يتم إنشاؤها أو لا يمكن إنشاؤها بعد. في الفيزياء الحيوية والبيولوجيا الهيكلية، يتم تطبيق الطريقة بشكل متكرر لدراسة حركات الجزيئات الكبيرة مثل البروتينات والأحماض النووية، والتي يمكن أن تكون مفيدة لتفسير نتائج بعض التجارب الفيزيائية الحيوية ونمذجة التفاعلات مع الجزيئات الأخرى، كما هو الحال في الإرساء الترابطي. من حيث المبدأ، يمكن استخدام الديناميكا الجزيئية للتنبؤ من البداية بهيكل البروتين عن طريق محاكاة طي سلسلة البولي ببتيد من ملف عشوائي.

يمكن اختبار نتائج محاكاة الديناميكا الجزيئية من خلال المقارنة مع التجارب التي تقيس الديناميكيات الجزيئية، والتي تعد طريقة شائعة منها هي التحليل الطيفي بالرنين المغناطيسي النووي. يمكن اختبار تنبؤات الهيكل المشتقة من الديناميكا الجزيئية من خلال تجارب على مستوى المجتمع في التقييم النقدي لتوقع بنية البروتين (CASP)، على الرغم من أن الطريقة قد حققت نجاحًا محدودًا تاريخيًا في هذا المجال. كتب مايكل ليفيت، الذي شارك في جائزة نوبل جزئياً لتطبيق الديناميكا الجزيئية على البروتينات، في عام 1999 أن المشاركين في التقدير التوقعي لهيكل البروتين لم يستخدموا الطريقة عادةً بسبب " ... إحراج مركزي للميكانيكا الجزيئية، أي تقليل الطاقة أو الديناميات الجزيئية بشكل عام يؤدي إلى نموذج أقل شبهاً بالهيكل التجريبي. " [10] أدت التحسينات في الموارد الحسابية التي تسمح بمسارات الديناميكا الجزيئية أكثر وأطول، جنبًا إلى جنب مع التحسينات الحديثة في جودة معلمات مجال القوة، إلى بعض التحسينات في كل من تنبؤ الهيكل وصقل نموذج التماثل، دون الوصول إلى نقطة الفائدة العملية في هذه المجالات؛ يحدد العديد معلمات مجال القوة كمجال رئيسي لمزيد من التطوير.[11][12][13]

تم الإبلاغ عن الديناميكا الجزيئية محاكاة ل الخاصة الدوائية تطوير وتصميم الأدوية.[14] على سبيل المثال، بينتو وآخرون نفذوا عمليات محاكاة الديناميكا الجزيئية لمجمعات (Bcl-Xl) لحساب متوسط مواضع الأحماض الأمينية الحرجة المشاركة في ربط الترابط.[15] من ناحية أخرى، كارلسون وآخرون. نفذت محاكاة الديناميكيات الجزيئية لتحديد المركبات التي تكمل المستقبل مع التسبب في الحد الأدنى من اضطراب التشكل والمرونة في الموقع النشط. تم تراكب لقطات من البروتين على فترات زمنية ثابتة أثناء المحاكاة لتحديد مناطق الربط المحفوظة (المحفوظة في ثلاثة إطارات على الأقل من أحد عشر إطارًا) لتطوير عالم الأدوية. سبيراكيس وآخرون يعتمد على سير عمل محاكاة الديناميكا الجزيئية، وبصمات الأصابع للروابط والبروتينات (FLAP) وتحليل التمييز الخطي لتحديد أفضل توافق بروتين يجند للعمل كقوالب صيدلانية استنادًا إلى تحليل (ROC) بأثر رجعي لعقاقير الصيدلانية الناتجة. في محاولة لتحسين نمذجة اكتشاف الأدوية القائمة على الهيكل، مقابل الحاجة إلى العديد من المركبات النموذجية، اقترح هاتمال مزيجًا من محاكاة الديناميكا الجزيئية وتحليل الاتصالات بين الجزيئات لمستقبلات ليجيند لتمييز الاتصالات الحرجة بين الجزيئات (تفاعلات الربط) من تلك الزائدة عن الحاجة في مركب واحد بروتين يجند. يمكن بعد ذلك تحويل جهات الاتصال الحرجة إلى نماذج صيدلانية يمكن استخدامها للفحص الافتراضي.[16]

ترتبط حدود الطريقة بمجموعات المعلمات المستخدمة، ومجالات قوة الميكانيكا الجزيئية الأساسية. تشغيل واحد لمحاكاة الديناميكا الجزيئية يعمل على تحسين الطاقة الكامنة، بدلاً من الطاقة المجانية للبروتين، مما يعني أن جميع المساهمات الحتمية في الاستقرار الديناميكي الحراري لبنية البروتين مهملة، بما في ذلك الانتروبيا المطابقة لسلسلة البولي ببتيد (العامل الرئيسي الذي يزعزع استقرار بنية البروتين) والتأثيرات الكارهة للماء (القوى الدافعة الرئيسية لطي البروتين).[17] عامل مهم آخر هو روابط الهيدروجين داخل الجزيئية، [18] والتي لم يتم تضمينها بشكل صريح في مجالات القوة الحديثة، ولكنها توصف بتفاعلات كولوم لشحنات النقطة الذرية. هذا تقدير تقريبي لأن الروابط الهيدروجينية لها طبيعة ميكانيكية وكيميائية جزئية. علاوة على ذلك، تُحسب التفاعلات الكهروستاتيكية عادةً باستخدام ثابت العزل الكهربائي للفراغ، على الرغم من أن المحلول المائي المحيط به ثابت عازل أعلى بكثير. باستخدام العيانية ثابت العزل الكهربائي على مسافات قصيرة بين الذرات غير مشكوك فيه. أخيرًا، عادةً ما يتم وصف تفاعلات قوى فان دير فالس في الديناميكا الجزيئية بواسطة إمكانات جهد لينارد-جونز استنادًا إلى نظرية فريتز لندن التي لا تنطبق إلا في الفراغ. ومع ذلك، فإن جميع أنواع قوى فان دير فال هي في نهاية المطاف من أصل إلكتروستاتيكي وبالتالي تعتمد على الخصائص العازلة للبيئة.[19] يوضح القياس المباشر لقوى الجذب بين المواد المختلفة (مثل ثابت هامكر) أن "التفاعل بين الهيدروكربونات عبر الماء يبلغ حوالي 10٪ من ذلك عبر الفراغ".[19] تم إهمال الاعتماد على البيئة لقوى فان دير فال في عمليات المحاكاة القياسية، ولكن يمكن تضمينها من خلال تطوير مجالات قوة قابلة للاستقطاب.

قيود التصميم

يجب أن يأخذ تصميم محاكاة الديناميكيات الجزيئية في الاعتبار القوة الحسابية المتاحة. يجب تحديد حجم المحاكاة (n = عدد الجسيمات)، والوقت، والمدة الزمنية الإجمالية بحيث يمكن إنهاء الحساب في غضون فترة زمنية معقولة. ومع ذلك، يجب أن تكون عمليات المحاكاة طويلة بما يكفي لتكون ذات صلة بالمقاييس الزمنية للعمليات الطبيعية قيد الدراسة. للحصول على استنتاجات صحيحة إحصائيًا من عمليات المحاكاة، يجب أن يتطابق المدى الزمني الذي تمت محاكاته مع حركية العملية الطبيعية. خلافًا لذلك، يكون الأمر مشابهًا للتوصل إلى استنتاجات حول كيفية سير الإنسان عندما ينظر فقط إلى أقل من خطوة واحدة. تستخدم معظم المنشورات العلمية حول ديناميكيات البروتينات والحمض النووي [20][21] بيانات من عمليات المحاكاة التي تمتد نانوثانية (10 ⁻⁹ ثوانٍ) إلى ميكروثانية (10 ⁶ ثوانٍ). للحصول على هذه المحاكاة، هناك حاجة إلى عدة أيام من وحدة المعالجة المركزية إلى سنوات وحدة المعالجة المركزية. تسمح الخوارزميات المتوازية بتوزيع الحمل بين وحدات المعالجة المركزية؛ مثال على ذلك هو خوارزمية التحلل المكاني أو القوة.[22]

أثناء محاكاة الديناميكا الجزيئية الكلاسيكية، فإن المهمة الأكثر كثافة لوحدة المعالجة المركزية هي تقييم الإمكانات كدالة للإحداثيات الداخلية للجسيمات. ضمن تقييم الطاقة هذا، يكون الجزء الأغلى هو الجزء غير المترابط أو غير التساهمي. في الكبير O التدوين، وديناميات الجزيئية المشتركة المحاكاة على نطاق و من قبل $O(n^{2})$ إذا كان كل الزوج الحكيم كهرباء وفان دير فال التفاعلات يجب أن تمثل بشكل واضح. يمكن تقليل هذه التكلفة الحسابية عن طريق استخدام طرق الكهرباء الساكنة مثل شبكة الجسيمات بتلخيص ايوالد ( $O(n\log(n))$ ) أو الجسيمات - الجسيمات - الجسيمات - الشبكة (P3M)، أو طرق القطع الكروية الجيدة ( $O(n)$ ).^{[بحاجة لمصدر]}

هناك عامل آخر يؤثر على إجمالي وقت وحدة المعالجة المركزية الذي تحتاجه المحاكاة وهو حجم الخطوة الزمنية للتكامل. هذه هي المدة الزمنية بين تقييمات الإمكانات. يجب اختيار الخطوة الزمنية صغيرة بما يكفي لتجنب أخطاء التقدير (أي أصغر من الفترة المتعلقة بأسرع تردد اهتزازي في النظام). الخطوات الزمنية النموذجية لـ الديناميكا الجزيئية الكلاسيكي بترتيب 1 فيمتوثانية (10 - ¹⁵ ثانية). يمكن توسيع هذه القيمة باستخدام الخوارزميات مثل خوارزمية قيود شيك، والتي تثبت اهتزازات الذرات الأسرع (على سبيل المثال، الهيدروجين) في مكانها. تم أيضًا تطوير طرق متعددة للمقياس الزمني، والتي تتيح فترات ممتدة بين تحديثات القوى البعيدة المدى الأبطأ.[23][24][25]

لمحاكاة الجزيئات في مذيب، يجب الاختيار بين المذيب الصريح والضمني. يجب حساب جسيمات المذيبات الصريحة (مثل نماذج المياه TIP3P و SPC / E وSPC-f) بشكل مكلف عن طريق مجال القوة، بينما تستخدم المذيبات الضمنية نهج المجال المتوسط. يعد استخدام مذيب صريح مكلفًا من الناحية الحسابية، ويتطلب تضمين ما يقرب من عشرة أضعاف الجسيمات في المحاكاة. لكن حبيبات ولزوجة المذيب الصريح ضروريان لإعادة إنتاج خصائص معينة للجزيئات الذائبة. هذا مهم بشكل خاص لإعادة إنتاج الخواص الحركية الكيميائية.

في جميع أنواع محاكاة الديناميكيات الجزيئية، يجب أن يكون حجم صندوق المحاكاة كبيرًا بما يكفي لتجنب آثار حالة الحدود. غالبًا ما يتم التعامل مع شروط الحدود عن طريق اختيار القيم الثابتة عند الحواف (والتي قد تسبب تشوهات)، أو عن طريق استخدام شروط الحدود الدورية حيث يعود جانب واحد من حلقات المحاكاة إلى الجانب الآخر، ومحاكاة مرحلة مجمعة (والتي قد تسبب آثارًا أيضًا).

تمثيل تخطيطي لأخذ عينات من سطح الطاقة الكامنة للنظام مع الديناميكيات الجزيئية (باللون الأحمر) مقارنة بطرق مونت كارلو (باللون الأزرق).

مجموعة متناهية الصغر (NVE)

في المجموعة المتناهية الصغر، يتم عزل النظام عن التغيرات في الشامات (N) والحجم (V) والطاقة (E). يتوافق مع عملية ثابتة الحرارة بدون تبادل حراري. يمكن النظر إلى مسار الديناميات الجزيئية المتناهية الصغر على أنه تبادل للطاقة الكامنة والحركية، مع الحفاظ على إجمالي الطاقة. لنظام من الجسيمات N مع الإحداثيات $X$ والسرعات $V$ ، يمكن كتابة الزوج التالي من المعادلات التفاضلية من الدرجة الأولى في تدوين نيوتن كـ

F(X)=-\nabla U(X)=M{\dot {V}}(t)

V(t)={\dot {X}}(t).

وظيفة الطاقة الكامنة $U(X)$ النظام هو دالة إحداثيات الجسيمات $X$ . يشار إليه ببساطة على أنه الإمكانات في الفيزياء، أو مجال القوة في الكيمياء. تأتي المعادلة الأولى من قوانين نيوتن للحركة. القوة $F$ يمكن حساب التأثير على كل جسيم في النظام على أنه التدرج السالب لـ $U(X)$ .

لكل خطوة زمنية، موضع كل جسيم $X$ والسرعة $V$ قد تتكامل مع طريقة تكامل سيمبلكتيك مثل تكامل فيرلت. التطور الزمني ل $X$ و $V$ يسمى المسار. بالنظر إلى المواقف الأولية (على سبيل المثال، من المعرفة النظرية) والسرعات (على سبيل المثال، غاوسي العشوائي)، يمكننا حساب جميع المواقف والسرعات المستقبلية (أو السابقة).

أحد مصادر الالتباس المتكررة هو معنى درجة الحرارة في الديناميكا الجزيئية. عادة لدينا خبرة في درجات الحرارة العيانية، والتي تنطوي على عدد كبير من الجسيمات. لكن درجة الحرارة هي كمية إحصائية. إذا كان هناك عدد كبير بما يكفي من الذرات، فيمكن تقدير درجة الحرارة الإحصائية من درجة الحرارة اللحظية، والتي يتم العثور عليها من خلال مساواة الطاقة الحركية للنظام _بـ nk B T / 2 حيث n هو عدد درجات الحرية للنظام.

تنشأ ظاهرة مرتبطة بدرجة الحرارة بسبب قلة عدد الذرات المستخدمة في محاكاة الديناميكا الجزيئية. على سبيل المثال، ضع في اعتبارك محاكاة نمو فيلم نحاسي بدءًا من ركيزة تحتوي على 500 ذرة وطاقة ترسيب تبلغ 100 فولت. في العالم الحقيقي، سيتم نقل 100 فولت من الذرة المودعة بسرعة ومشاركتها بين عدد كبير من الذرات ( $10^{10}$ أو أكثر) دون تغيير كبير في درجة الحرارة. عندما يكون هناك 500 ذرة فقط، فإن الركيزة تتبخر على الفور تقريبًا بواسطة الترسب. يحدث شيء مشابه في عمليات المحاكاة الفيزيائية الحيوية. يتم رفع درجة حرارة النظام في (NVE) بشكل طبيعي عندما تخضع الجزيئات الكبيرة مثل البروتينات لتغيرات وترابط طارد للحرارة.

المجموعة المتعارف عليها (NVT)

في المجموعة المتعارف عليها، يتم حفظ كمية المادة (N) والحجم (V) ودرجة الحرارة (T). كما يطلق عليه أحيانًا الديناميكيات الجزيئية ذات درجة الحرارة الثابتة (CTالديناميكا الجزيئية). في (NVT)، يتم تبادل طاقة العمليات الماصة للحرارة والطاردة للحرارة مع منظم الحرارة.

تتوفر مجموعة متنوعة من خوارزميات الترموستات لإضافة الطاقة وإزالتها من حدود محاكاة الديناميكا الجزيئية بطريقة أكثر أو أقل واقعية، بالقرب من المجموعة المتعارف عليها. تشمل الأساليب الشائعة للتحكم في درجة الحرارة إعادة قياس السرعة، ترموستات نوزيه هوفر، وسلاسل نوزيه هوفر، وترموستات بيرندسن، وديناميكيات أندرسن ولانجفين. قد يقدم منظم الحرارة بيرندسن تأثير مكعب الثلج الطائر، والذي يؤدي إلى ترجمات غير مادية وتناوب للنظام المحاكي.

ليس من التافه الحصول على توزيع متعارف عليه للمطابقة والسرعات باستخدام هذه الخوارزميات. كيف يعتمد ذلك على حجم النظام واختيار منظم الحرارة ومعلمات منظم الحرارة وخطوة الوقت والمتكامل هو موضوع العديد من المقالات في هذا المجال.

مجموعة متساوية الحرارة متساوية الضغط (NPT)

يتم الحفاظ على كمية المادة (N) والضغط (P) ودرجة الحرارة (T) في المجموعة متساوي الحرارة - متساوي الضغط. بالإضافة إلى منظم الحرارة، هناك حاجة إلى باروستات. يتوافق بشكل وثيق مع ظروف المختبر مع وجود دورق مفتوح لدرجة الحرارة والضغط المحيطين.

في محاكاة الأغشية البيولوجية، فإن التحكم في الضغط الخواص غير مناسب. بالنسبة لطبقات الدهون الثنائية، يحدث التحكم في الضغط تحت منطقة غشاء ثابتة (NPAT) أو توتر سطحي ثابت "جاما" (NPγT).

المجموعات المعممة

طريقة تبادل النسخ المتماثلة هي مجموعة معممة. تم إنشاؤه في الأصل للتعامل مع الديناميكيات البطيئة لأنظمة الدوران المضطربة. يطلق عليه أيضًا التقسية الموازية. تحاول صياغة الديناميكا الجزيئية للتبادل المتماثل [26] التغلب على مشكلة الحدود الدنيا المتعددة من خلال تبادل درجة حرارة النسخ المتماثلة غير المتفاعلة للنظام التي تعمل في درجات حرارة متعددة.

الإمكانات في محاكاة الديناميكا الجزيئية

تتطلب محاكاة الديناميكيات الجزيئية تعريف وظيفة محتملة، أو وصفًا للمصطلحات التي تتفاعل بها الجسيمات في المحاكاة. في الكيمياء والبيولوجيا، يُشار إلى هذا عادةً باسم مجال القوة وفي فيزياء المواد على أنه جهد بين الذرات. يمكن تحديد الإمكانات على مستويات عديدة من الدقة المادية؛ تلك الأكثر شيوعًا في الكيمياء تعتمد على الميكانيكا الجزيئية وتجسد العلاج الميكانيكي الكلاسيكي لتفاعلات الجسيمات والجسيمات التي يمكن أن تعيد إنتاج التغييرات الهيكلية والتكوينية ولكن لا يمكنها عادةً إعادة إنتاج التفاعلات الكيميائية.

يستلزم الاختزال من الوصف الكمي الكامل إلى الإمكانات الكلاسيكية تقريبيين رئيسيين. الأول هو تقريب بورن أوبنهايمر، الذي ينص على أن ديناميكيات الإلكترونات سريعة جدًا بحيث يمكن اعتبارها تتفاعل على الفور مع حركة نواتها. نتيجة لذلك، يمكن معاملتهم بشكل منفصل. الثاني يتعامل مع النوى، وهي أثقل بكثير من الإلكترونات، على أنها جسيمات نقطية تتبع الديناميكيات النيوتونية الكلاسيكية. في الديناميكيات الجزيئية الكلاسيكية، يتم تقريب تأثير الإلكترونات كسطح طاقة كامن، وعادة ما يمثل الحالة الأرضية.

عندما تكون هناك حاجة إلى مستويات أدق من التفاصيل، يتم استخدام الإمكانات القائمة على ميكانيكا الكم ؛ تحاول بعض الطرق إنشاء إمكانات كلاسيكية / كمومية هجينة حيث يتم معالجة الجزء الأكبر من النظام بشكل كلاسيكي ولكن يتم التعامل مع منطقة صغيرة كنظام كمي، وعادةً ما تخضع لعملية تحول كيميائي.

الإمكانات التجريبية

كثيرا ما تسمى الإمكانات التجريبية المستخدمة في الكيمياء مجالات القوة، في حين أن تلك المستخدمة في فيزياء المواد تسمى الجهود بين الذرية.

معظم مجالات القوة في الكيمياء تجريبية وتتكون من مجموع القوى المرتبطة المرتبطة بالروابط الكيميائية وزوايا الرابطة وثنائيات السندات والقوى غير المرتبطة المرتبطة بقوى فان دير فال والشحنة الكهروستاتيكية. تمثل الإمكانات التجريبية تأثيرات ميكانيكا الكم بطريقة محدودة من خلال التقريبات الوظيفية المخصصة. تحتوي هذه الإمكانات على معلمات مجانية مثل الشحنة الذرية، ومعلمات فان دير فالس التي تعكس تقديرات نصف القطر الذري، وطول رابطة التوازن، والزاوية، وثنائي السطوح ؛ يتم الحصول عليها عن طريق التوافق مع الحسابات الإلكترونية التفصيلية (المحاكاة الكيميائية الكمومية) أو الخصائص الفيزيائية التجريبية مثل الثوابت المرنة والمعلمات الشبكية والقياسات الطيفية.

بسبب الطبيعة غير المحلية للتفاعلات غير المرتبطة، فإنها تنطوي على تفاعلات ضعيفة على الأقل بين جميع الجسيمات في النظام. عادة ما يكون حسابه هو عنق الزجاجة في سرعة محاكاة الديناميكا الجزيئية. لخفض التكلفة الحسابية، تستخدم حقول القوة تقديرات تقريبية رقمية مثل نصف قطر القطع المغير، أو خوارزميات مجال التفاعل، أو تجميع ايوالد لشبكة الجسيمات، أو شبكة الجسيمات والجسيمات والجسيمات الأحدث (P3M).

تستخدم حقول القوة الكيميائية عادةً ترتيبات ارتباط محددة مسبقًا (استثناء هو ديناميكيات طرق كيمياء الكم)، وبالتالي فهي غير قادرة على نمذجة عملية كسر الرابطة الكيميائية والتفاعلات بشكل صريح. من ناحية أخرى، يمكن للعديد من الإمكانات المستخدمة في الفيزياء، مثل تلك القائمة على شكلية ترتيب السندات، أن تصف عدة تنسيقات مختلفة للنظام وكسر الرابطة.[27][28] تتضمن أمثلة هذه الإمكانات إمكانات برينر [29] للهيدروكربونات وتطوراتها الإضافية لأنظمة C-Si-H [30] و COH.[31] يمكن اعتبار إمكانات [32] هجينًا كامل التفاعل بين إمكانات ترتيب الرابطة ومجالات القوة الكيميائية.

قم بإقران الإمكانات مقابل إمكانات الأجسام المتعددة

تتم صياغة الوظائف المحتملة التي تمثل الطاقة غير المرتبطة كمجموع على التفاعلات بين جسيمات النظام. أبسط خيار، مستخدم في العديد من مجالات القوة الشائعة، هو "جهد الزوج"، حيث يمكن حساب إجمالي الطاقة الكامنة من مجموع مساهمات الطاقة بين أزواج الذرات. لذلك، تسمى حقول القوة هذه أيضًا "حقول القوة المضافة". مثال على مثل هذا الزوج المحتمل هو احتمال جهد لينارد-جونز غير المرتبط (يُطلق عليه أيضًا احتمال 6-12)، المستخدم لحساب قوى فان دير فال.

U(r)=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]

مثال آخر هو نموذج Born (الأيوني) للشبكة الأيونية. المصطلح الأول في المعادلة التالية هو قانون كولوم لزوج من الأيونات، والمصطلح الثاني هو التنافر قصير المدى الذي شرحه مبدأ استبعاد باولي والمصطلح الأخير هو مصطلح تفاعل التشتت. عادةً ما تتضمن المحاكاة المصطلح ثنائي القطب فقط، على الرغم من تضمين المصطلح رباعي الأقطاب في بعض الأحيان.[33][34] عندما ن _ل = 6، وتسمى هذه الإمكانية أيضا إمكانية كولوم-باكنغهام.

U_{ij}(r_{ij})={\frac {z_{i}z_{j}}{4\pi \epsilon _{0}}}{\frac {1}{r_{ij}}}+A_{l}\exp {\frac {-r_{ij}}{p_{l}}}+C_{l}r_{ij}^{-n_{l}}+\cdots

في إمكانات الجسم المتعددة، تشتمل الطاقة الكامنة على تأثيرات ثلاثة أو أكثر من الجسيمات التي تتفاعل مع بعضها البعض.[35] في عمليات المحاكاة ذات الإمكانات الزوجية، توجد أيضًا تفاعلات عالمية في النظام، ولكنها تحدث فقط من خلال المصطلحات الزوجية. في إمكانات الأجسام المتعددة، لا يمكن العثور على الطاقة الكامنة بمجموع على أزواج من الذرات، حيث يتم حساب هذه التفاعلات بشكل صريح على أنها مزيج من المصطلحات ذات الترتيب الأعلى. في العرض الإحصائي، لا يمكن التعبير عن التبعية بين المتغيرات بشكل عام باستخدام المنتجات المزدوجة فقط من درجات الحرية. على سبيل المثال، إمكانات تيرسوف، [36] التي كانت تُستخدم في الأصل لمحاكاة الكربون، والسيليكون، والجرمانيوم، ومنذ ذلك الحين تم استخدامها لمجموعة واسعة من المواد الأخرى، تتضمن مجموع مجموعات من ثلاث ذرات، مع وجود زوايا بين الذرات عامل مهم في الإمكانات. ومن الأمثلة الأخرى طريقة الذرة المدمجة (EAM)، [37] (EDIP)، [35] وإمكانات تقريب اللحظات الثانية المحكم الربط (TBSMA)، [38] حيث تكون كثافة الإلكترون للحالات في منطقة الذرة هي محسوبة من مجموع المساهمات من الذرات المحيطة، وبالتالي فإن مساهمة الطاقة الكامنة هي دالة لهذا المجموع.

الإمكانات شبه التجريبية

تستفيد الإمكانات شبه التجريبية من تمثيل المصفوفة من ميكانيكا الكم. ومع ذلك، يتم العثور على قيم عناصر المصفوفة من خلال الصيغ التجريبية التي تقدر درجة التداخل في المدارات الذرية المحددة. يتم بعد ذلك مائل المصفوفة لتحديد شغل المدارات الذرية المختلفة، ويتم استخدام الصيغ التجريبية مرة أخرى لتحديد مساهمات الطاقة في المدارات.

هناك مجموعة متنوعة من الإمكانات شبه التجريبية، تسمى إمكانات الربط المحكم، والتي تختلف وفقًا للذرات التي يتم نمذجتها.

إمكانات الاستقطاب

تتضمن معظم مجالات القوة الكلاسيكية ضمنيًا تأثير الاستقطاب، على سبيل المثال، عن طريق زيادة الشحنات الجزئية التي تم الحصول عليها من الحسابات الكيميائية الكمومية. هذه الشحنات الجزئية ثابتة بالنسبة إلى كتلة الذرة. ولكن يمكن لمحاكاة الديناميات الجزيئية أن تكون نموذجًا صريحًا لقابلية الاستقطاب مع إدخال ثنائيات الأقطاب المستحثة من خلال طرق مختلفة، مثل الجسيمات الدقيقة أو الشحنات المتقلبة. هذا يسمح بإعادة التوزيع الديناميكي للشحنة بين الذرات والتي تستجيب للبيئة الكيميائية المحلية.

لسنوات عديدة، تم وصف عمليات محاكاة الديناميكا الجزيئية القابلة للاستقطاب على أنها الجيل التالي. بالنسبة للسوائل المتجانسة مثل الماء، تم تحقيق دقة متزايدة من خلال إدراج قابلية الاستقطاب.[39][40][41] كما تم تحقيق بعض النتائج الواعدة للبروتينات.[42][43] ومع ذلك، لا يزال من غير المؤكد أفضل طريقة لتقريب الاستقطاب في المحاكاة.

الإمكانات في طرق كيمياء الكم

في الديناميكيات الجزيئية الكلاسيكية، يتم تمثيل سطح طاقة كامنة (عادةً الحالة الأرضية) في مجال القوة. هذا نتيجة لتقريب بورن أوبنهايمر. في الحالات المثارة أو التفاعلات الكيميائية أو عند الحاجة إلى تمثيل أكثر دقة، يمكن الحصول على السلوك الإلكتروني من المبادئ الأولى باستخدام طريقة ميكانيكا الكم، مثل نظرية الكثافة الوظيفية. يسمى هذا الديناميكيات الجزيئية لكيمياء الكم. نظرًا لتكلفة معالجة درجات الحرية الإلكترونية، فإن العبء الحسابي لهذه المحاكاة أعلى بكثير من الديناميكيات الجزيئية التقليدية. لهذا السبب، عادةً ما يقتصر نظام الديناميكا الجزيئية على أنظمة أصغر وأوقات أقصر.

يمكن استخدام الطرق الميكانيكية والكيميائية الكمومية للمبتدئين لحساب الطاقة الكامنة لنظام أثناء الطيران، حسب الحاجة للتوافق في المسار. يتم إجراء هذا الحساب عادةً في الجوار القريب لإحداثيات التفاعل. على الرغم من أنه يمكن استخدام تقديرات تقريبية مختلفة، إلا أنها تستند إلى اعتبارات نظرية، وليس على ملاءمة تجريبية. تنتج حسابات كيمياء الكم قدرًا هائلاً من المعلومات غير المتوفرة من الأساليب التجريبية، مثل كثافة الحالات الإلكترونية أو الخصائص الإلكترونية الأخرى. من المزايا المهمة لاستخدام طرق كيمياء الكم القدرة على دراسة التفاعلات التي تتضمن كسر أو تكوين روابط تساهمية، والتي تتوافق مع حالات إلكترونية متعددة. علاوة على ذلك، تسمح طرق كيمياء الكم أيضًا باستعادة التأثيرات التي تتجاوز تقريب بورن-أوبنهايمر باستخدام مناهج مثل الديناميكيات الكمومية الكلاسيكية المختلطة.

هجين QM / MM

تعتبر طرق QM (ميكانيكا الكم) قوية جدًا. ومع ذلك، فهي مكلفة من الناحية الحسابية، في حين أن طرق MM (الميكانيكا الكلاسيكية أو الجزيئية) سريعة ولكنها تعاني من عدة حدود (تتطلب معايير واسعة النطاق ؛ تقديرات الطاقة التي تم الحصول عليها ليست دقيقة للغاية ؛ لا يمكن استخدامها لمحاكاة التفاعلات حيث يتم كسر / تشكيل الروابط التساهمية ؛ ومحدودي قدراتهم على تقديم تفاصيل دقيقة فيما يتعلق بالبيئة الكيميائية). ظهرت فئة جديدة من الأساليب التي تجمع بين النقاط الجيدة في حسابات QM (الدقة) و MM (السرعة). تسمى هذه الطرق طرق ميكانيكا الكم الميكانيكية والجزيئية المختلطة أو المختلطة (الهجين QM / MM).[44]

إن أهم ميزة لطريقة إدارة الجودة (QM / MM) الهجينة هي السرعة. تكلفة عمل الديناميكيات الجزيئية الكلاسيكية (MM) في مقاييس الحالة الأكثر وضوحًا O (n ²)، حيث n هو عدد الذرات في النظام. هذا يرجع أساسًا إلى مصطلح التفاعلات الكهروستاتيكية (يتفاعل كل جسيم مع كل جسيم آخر). ومع ذلك، فإن استخدام نصف قطر القطع والتحديثات الدورية لقائمة الأزواج ومؤخرًا الاختلافات في طريقة شبكة الجسيمات ايوالد (PME) قد قلل هذا إلى ما بين O (n) إلى O (n ²). بمعنى آخر، إذا تمت محاكاة نظام به ضعف عدد الذرات، فسيستغرق ما بين ضعفين إلى أربعة أضعاف قوة الحوسبة. من ناحية أخرى، فإن أبسط حسابات كيمياء الكم مقياس نموذجي O (n ³) أو أسوأ (تم اقتراح حسابات هارتري فوك المقيدة لتوسيع نطاق ~ O (n ^2.7)). للتغلب على هذا الحد، يتم التعامل مع جزء صغير من النظام ميكانيكيًا (عادةً موقع نشط من الإنزيم) ويتم معالجة النظام المتبقي بشكل كلاسيكي.

في التطبيقات الأكثر تعقيدًا، توجد طرق QM / MM لمعالجة كل من النوى الخفيفة المعرضة للتأثيرات الكمومية (مثل الهيدروجين) والحالات الإلكترونية. هذا يسمح بتوليد وظائف موجات الهيدروجين (على غرار وظائف الموجة الإلكترونية). كانت هذه المنهجية مفيدة في التحقيق في ظواهر مثل نفق الهيدروجين. أحد الأمثلة حيث قدمت طرق QM / MM اكتشافات جديدة هو حساب نقل الهيدريد في إنزيم نازع هيدروجين الكحول في الكبد. في هذه الحالة، نفق الكم مهم للهيدروجين، لأنه يحدد معدل التفاعل.[45]

الخشنة الحبيبات والتمثيلات المخفضة

في الطرف الآخر من مقياس التفاصيل توجد نماذج ذات حبيبات خشنة ونماذج شعرية. بدلاً من التمثيل الصريح لكل ذرة في النظام، يستخدم المرء "ذرات زائفة" لتمثيل مجموعات من الذرات. قد تتطلب عمليات محاكاة الديناميكا الجزيئية على أنظمة كبيرة جدًا موارد كمبيوتر كبيرة بحيث لا يمكن دراستها بسهولة من خلال طرق كل الذرة التقليدية. وبالمثل، فإن محاكاة العمليات على نطاقات زمنية طويلة (تتجاوز حوالي 1 ميكرو ثانية) باهظة التكلفة، لأنها تتطلب الكثير من الخطوات الزمنية. في هذه الحالات، يمكن للمرء أحيانًا معالجة المشكلة باستخدام تمثيلات مختصرة، والتي تسمى أيضًا نماذج الحبيبات الخشنة.[46]

من الأمثلة على طرق الحبيبات الخشنة (CG) الديناميكيات الجزيئية المتقطعة (CG-Dالديناميكا الجزيئية) [47][48] ونماذج Go.[49] يتم إجراء الحبيبات الخشنة أحيانًا بأخذ ذرات زائفة أكبر. تم استخدام مثل هذه التقريبات الذرية الموحدة في محاكاة الديناميكا الجزيئية للأغشية البيولوجية. قد يكون تنفيذ مثل هذا النهج على الأنظمة التي تكون فيها الخصائص الكهربائية ذات أهمية أمرًا صعبًا نظرًا لصعوبة استخدام توزيع الشحنة المناسب على الذرات الزائفة.[50] يتم تمثيل ذيول الليبيدات الأليفاتية بواسطة عدد قليل من الذرات الزائفة عن طريق تجميع 2 إلى 4 مجموعات ميثيلين في كل ذرة زائفة.

يجب أن يتم تحديد معلمات هذه النماذج الخشنة للغاية بشكل تجريبي، من خلال مطابقة سلوك النموذج مع البيانات التجريبية المناسبة أو محاكاة جميع الذرة. من الناحية المثالية، يجب أن تأخذ هذه المعلمات في الاعتبار المساهمات الحرارية والنتروبية في الطاقة الحرة بطريقة ضمنية.[51] عندما يتم إجراء الحبيبات الخشنة على مستويات أعلى، قد تكون دقة الوصف الديناميكي أقل موثوقية. ولكن تم استخدام النماذج ذات الحبيبات الخشنة بنجاح لفحص مجموعة واسعة من الأسئلة في البيولوجيا الهيكلية وتنظيم البلورات السائلة وزجاج البوليمر.

أمثلة على تطبيقات الحبيبات الخشنة:

غالبًا ما تُجرى دراسات طي البروتين ودراسات التنبؤ ببنية البروتين باستخدام ذرة زائفة واحدة أو بضع ذرات لكل حمض أميني.[46]
تم فحص انتقالات الطور البلوري السائل في الأشكال الهندسية المحصورة و / أو أثناء التدفق باستخدام إمكانات جاي بيرن، التي تصف الأنواع متباينة الخواص.
تمت دراسة زجاج البوليمر أثناء التشوه باستخدام نوابض توافقية بسيطة أو نوابض فين لتوصيل الكرات الموصوفة بواسطة إمكانات لينارد جونز.
تم فحص الالتفاف الفائق للحمض النووي باستخدام 1-3 ذرات زائفة لكل زوج أساس، وبدقة أقل.
تم فحص تغليف الحمض النووي المزدوج الحلزوني في العاثية بنماذج حيث تمثل الذرة الزائفة منعطفًا واحدًا (حوالي 10 أزواج أساسية) من الحلزون المزدوج.
تم تصميم بنية الحمض النووي الريبي في الريبوسوم والأنظمة الكبيرة الأخرى باستخدام ذرة زائفة واحدة لكل نوكليوتيد.
محاكاة افتراضية للخلية لدراسة تفاعل الخلايا والركائز المختلفة.[52]

أبسط شكل من أشكال الحبيبات الخشنة هو الذرة المتحدة (تسمى أحيانًا الذرة الممتدة)، وقد تم استخدامها في معظم عمليات محاكاة الديناميكا الجزيئية المبكرة للبروتينات والدهون والأحماض النووية. على سبيل المثال، بدلاً من معالجة جميع الذرات الأربع _{لمجموعة ميثيل CH 3} بشكل صريح (أو جميع الذرات الثلاث _{لمجموعة الميثيلين CH 2})، يمثل المرء المجموعة بأكملها بذرة زائفة واحدة. يجب بالطبع تحديد معلماتها بشكل صحيح بحيث تتمتع تفاعلاتها مع المجموعات الأخرى بالاعتماد المناسب على المسافة. تنطبق اعتبارات مماثلة على الروابط والزوايا والالتواءات التي تشارك فيها الذرة الزائفة. في هذا النوع من التمثيل الذري الموحد، يزيل المرء عادةً جميع ذرات الهيدروجين الصريحة باستثناء تلك التي لديها القدرة على المشاركة في الروابط الهيدروجينية (الهيدروجين القطبي). مثال على ذلك هو مجال القوة تشارم 19.

عادةً ما يتم الاحتفاظ بالهيدروجين القطبي في النموذج، لأن المعالجة المناسبة للروابط الهيدروجينية تتطلب وصفًا دقيقًا بشكل معقول للاتجاه والتفاعلات الكهروستاتيكية بين مجموعات المتبرع والمستقبل. يمكن لمجموعة الهيدروكسيل، على سبيل المثال، أن تكون مانحًا لرابطة الهيدروجين، ومتقبلًا لرابطة الهيدروجين، وسيكون من المستحيل معالجة ذلك باستخدام ذرة زائفة (OH) واحدة. حوالي نصف الذرات الموجودة في البروتين أو الحمض النووي هي هيدروجين غير قطبي، لذا فإن استخدام الذرات الموحدة يمكن أن يوفر توفيرًا كبيرًا في وقت الكمبيوتر.

دمج تأثيرات المذيبات

في العديد من عمليات محاكاة نظام المذيب المذاب، ينصب التركيز الرئيسي على سلوك المذاب مع القليل من الاهتمام بسلوك المذيب خاصة في جزيئات المذيب الموجودة في مناطق بعيدة عن الجزيء المذاب.[53] قد تؤثر المذيبات على السلوك الديناميكي للمذابات من خلال الاصطدامات العشوائية وفرض مقاومة احتكاكية على حركة المذاب عبر المذيب. يمكن أن يساعد استخدام شروط الحدود الدورية غير المستطيلة والحدود العشوائية وأغلفة المذيبات في تقليل عدد جزيئات المذيبات المطلوبة وتمكين نسبة أكبر من وقت الحوسبة ليتم إنفاقها بدلاً من ذلك في محاكاة المذاب. من الممكن أيضًا دمج تأثيرات المذيب دون الحاجة إلى وجود أي جزيئات مذيب واضحة. أحد الأمثلة على هذا النهج هو استخدام القوة المتوسطة المحتملة (PMF) التي تصف كيفية تغير الطاقة الحرة كتنوع إحداثيات معينة. يحتوي تغيير الطاقة الحرة الموصوف بواسطة (PMF) على متوسط تأثيرات المذيب.

قوى بعيدة المدى

التفاعل طويل المدى هو تفاعل لا يسقط فيه التفاعل المكاني أسرع من $r^{-d}$ أين $d$ هي أبعاد النظام. تشمل الأمثلة تفاعلات الشحنة والشحنة بين الأيونات وتفاعلات ثنائي القطب بين الجزيئات. تمثل نمذجة هذه القوى تحديًا كبيرًا لأنها كبيرة على مسافة قد تكون أكبر من نصف طول الصندوق مع محاكاة لعدة آلاف من الجسيمات. على الرغم من أن أحد الحلول سيكون زيادة حجم طول الصندوق بشكل كبير، إلا أن أسلوب القوة الغاشمة هذا أقل من مثالي لأن المحاكاة ستصبح باهظة الثمن من الناحية الحسابية. إن اقتطاع الإمكانات كرويًا هو أيضًا غير وارد حيث يمكن ملاحظة السلوك غير الواقعي عندما تكون المسافة قريبة من مسافة القطع.[54]

الديناميكات الجزيئية الموجهة (SMD)

تقوم محاكاة الديناميكيات الجزيئية (Sالديناميكا الجزيئية)، أو محاكاة مسبار القوة، بتطبيق قوى على بروتين من أجل التلاعب بهيكله عن طريق سحبه على طول درجات الحرية المرغوبة. يمكن استخدام هذه التجارب للكشف عن التغيرات الهيكلية في البروتين على المستوى الذري. غالبًا ما يستخدم Sالديناميكا الجزيئية لمحاكاة أحداث مثل التكشف أو التمدد الميكانيكي.[55]

هناك نوعان من البروتوكولات النموذجية لـ الديناميكا الجزيئية: أحدهما تكون فيه سرعة السحب ثابتة، والآخر تكون فيه القوة المطبقة ثابتة. بشكل نموذجي، يتم تقييد جزء من النظام المدروس (على سبيل المثال، ذرة في بروتين) بواسطة جهد توافقي. ثم يتم تطبيق القوى على ذرات معينة إما بسرعة ثابتة أو بقوة ثابتة. يتم استخدام أخذ العينات الشامل لتحريك النظام على طول تنسيق التفاعل المطلوب عن طريق تغيير، على سبيل المثال، القوى والمسافات والزوايا التي تم التلاعب بها في المحاكاة. من خلال أخذ العينات المظلة، يتم أخذ عينات من جميع تكوينات النظام - عالية الطاقة ومنخفضة الطاقة - بشكل كافٍ. بعد ذلك، يمكن حساب تغيير كل تكوين في الطاقة الحرة على أنه احتمال متوسط القوة.[56] إحدى الطرق الشائعة لحساب (PMF) هي من خلال طريقة تحليل الرسم البياني الموزون (WHAM)، والتي تحلل سلسلة من محاكاة أخذ العينات الشاملة.[57][58]

يوجد الكثير من التطبيقات المهمة لـ Sالديناميكا الجزيئية في مجال اكتشاف الأدوية وعلوم الجزيئات الحيوية. على سبيل المثال تم استخدام Sالديناميكا الجزيئية للتحقيق في استقرار ليفية الزهايمر الأولية، [59] لدراسة تفاعل بروتين يجند في كيناز المعتمد على السيكلين 5 [60] وحتى لإظهار تأثير المجال الكهربائي على مركب الثرومبين (البروتين) والأبتامر (النيوكليوتيد) [61] بين العديد من الدراسات الأخرى المثيرة للاهتمام.

أمثلة على التطبيقات

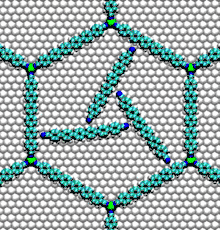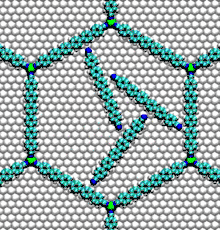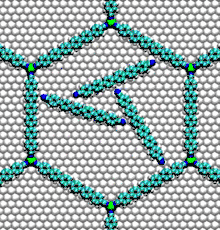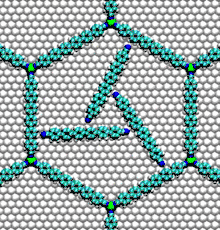
محاكاة الديناميكيات الجزيئية لمحرك جزيئي اصطناعي يتكون من ثلاثة جزيئات في ثقب نانوي (القطر الخارجي 6.7 نانومتر) عند 250 كلفن.

تستخدم الديناميات الجزيئية في العديد من مجالات العلوم.

تم نشر أول محاكاة الديناميكا الجزيئية لعملية الطي البيولوجي المبسطة في عام 1975. مهدت المحاكاة التي نُشرت في دورية نتشر الطريق لمساحة واسعة من طي البروتين الحسابي الحديث.[62]
تم نشر أول محاكاة الديناميكا الجزيئية لعملية بيولوجية في عام 1976. مهدت المحاكاة التي نُشرت في دورية نتشر الطريق لفهم حركة البروتين باعتبارها ضرورية في الوظيفة وليس مجرد ملحق.[63]
الديناميكا الجزيئية هي الطريقة القياسية لمعالجة شلالات الاصطدام في نظام ارتفاع الحرارة، أي التأثيرات التي تحدثها إشعاعات النيوترونات والأيونات النشطة على المواد الصلبة والأسطح الصلبة.[64]

توضح الأمثلة الفيزيائية الحيوية التالية الجهود الملحوظة لإنتاج محاكاة لأنظمة ذات حجم كبير جدًا (فيروس كامل) أو أوقات محاكاة طويلة جدًا (تصل إلى 1.112 مللي ثانية):

محاكاة الديناميكا الجزيئية لفيروس فسيفساء التبغ الساتلي الكامل (STMV) (2006، الحجم: 1 مليون ذرة، وقت المحاكاة: 50 نانوثانية، البرنامج: NAالديناميكا الجزيئية) هذا الفيروس عبارة عن فيروس نباتي صغير عشروني الوجوه يؤدي إلى تفاقم أعراض الإصابة بفيروس التبغ الفسيفسائي (TMV). تم استخدام محاكاة الديناميكيات الجزيئية لاستكشاف آليات التجمع الفيروسي. يتكون جسيم STMV بأكمله من 60 نسخة متطابقة من بروتين واحد يتكون من القفيصة الفيروسية (الغلاف)، وجينوم RNA أحادي النوكليوتيد 1063 تقطعت به السبل. تتمثل إحدى النتائج الرئيسية في أن الكابسيد يكون غير مستقر للغاية عند عدم وجود RNA بداخله. ستستغرق المحاكاة جهاز كمبيوتر مكتبي واحدًا في عام 2006 حوالي 35 عامًا حتى تكتمل. وهكذا تم القيام به في العديد من المعالجات بالتوازي مع التواصل المستمر بينهم.[65]
محاكاة قابلة للطي لـ فيلين هيدبيس بتفاصيل شاملة (2006، الحجم: 20000 ذرة ؛ وقت المحاكاة: 500 ميكرو ثانية = 500000 نانوثانية، البرنامج: فولدنغ@هوم) تم تشغيل هذه المحاكاة في 200000 وحدة معالجة مركزية من أجهزة الكمبيوتر الشخصية المشاركة حول العالم. تم تثبيت برنامج فولدنغ@هوم على أجهزة الكمبيوتر هذه، وهو جهد حوسبي موزع على نطاق واسع بتنسيق من فيجاي باندي في جامعة ستانفورد. تم فحص الخصائص الحركية لبروتين فيلين هيدبيس باستخدام العديد من المسارات المستقلة والقصيرة التي تديرها وحدة المعالجة المركزية دون اتصال مستمر في الوقت الحقيقي. كانت إحدى الطرق المستخدمة هي تحليل قيمة بفولد، والتي تقيس احتمالية الطي قبل الكشف عن تشكيل بداية محدد. يعطي بفولد معلومات حول هياكل الحالة الانتقالية وترتيب المطابقة على طول مسار الطي. يمكن أن يكون كل مسار في حساب بفولد قصيرًا نسبيًا، ولكن هناك حاجة إلى العديد من المسارات المستقلة.[66]
تم إجراء عمليات محاكاة طويلة للمسار المستمر على انطون، وهو كمبيوتر عملاق متوازي بشكل كبير تم تصميمه وبنائه حول دوائر متكاملة خاصة بالتطبيقات المخصصة (ASIC) ووصلات متصلة بواسطة دي شو للأبحاث. أطول نتيجة تم نشرها لمحاكاة تم إجراؤها باستخدام أنطون هي محاكاة NTL9 تبلغ 1.112 مللي ثانية عند 355 كلفن ؛ تم أيضًا إجراء محاكاة ثانية مستقلة تبلغ 1.073 مللي ثانية لهذا التكوين (والعديد من عمليات المحاكاة الأخرى لأكثر من 250 ميكرو ثانية من الوقت الكيميائي المستمر).[67] في كيف تطوى البروتينات سريعة الطي، يناقش الباحثون كريستين ليندورف لارسن وستيفانو بيانا ورون أو درور وديفيد إي. تكشف عن مجموعة من المبادئ المشتركة الكامنة وراء طي 12 بروتينًا متنوعًا هيكليًا ". يسمح فحص هذه المسارات الطويلة المتنوعة، التي تم تمكينها بواسطة أجهزة مخصصة ومخصصة، باستنتاج أنه "في معظم الحالات، يتبع الطي مسارًا واحدًا مهيمنًا تظهر فيه عناصر الهيكل الأصلي بترتيب مرتبط بشدة بميلها للتشكل في تكشفت الدولة ".[67] في دراسة منفصلة، تم استخدام أنطون لإجراء محاكاة 1.013 مللي ثانية لديناميات الحالة الأصلية لمثبط التربسين البنكرياس البقري (BPTI) عند 300 كلفن.[68]

يستفيد تطبيق مهم آخر لطريقة الديناميكا الجزيئية من قدرتها على التوصيف ثلاثي الأبعاد وتحليل التطور المجهرية على النطاق الذري.

تُستخدم محاكاة الديناميكا الجزيئية في توصيف تطور حجم الحبوب، على سبيل المثال، عند وصف التآكل والاحتكاك لمواد Al و Al (Zr) النانوية. يتم تحليل تطور الخلع وتطور حجم الحبيبات أثناء عملية الاحتكاك في هذه المحاكاة. نظرًا لأن طريقة الديناميكا الجزيئية قدمت المعلومات الكاملة للبنية المجهرية، فقد تم حساب تطور حجم الحبيبات في صورة ثلاثية الأبعاد باستخدام مطابقة القالب متعدد السطوح، وتجزئة الحبوب، وتجميع الرسم البياني . في مثل هذه المحاكاة، قدمت طريقة الديناميكا الجزيئية قياسًا دقيقًا لحجم الحبوب. من خلال الاستفادة من هذه المعلومات، تم استخراج الهياكل الفعلية للحبوب وقياسها وتقديمها. مقارنة بالطريقة التقليدية لاستخدام الديناميكات الجزيئية الموجهة (SMD) مع شريحة واحدة ثنائية الأبعاد من المادة، يوفر الديناميكا الجزيئية طريقة ثلاثية الأبعاد ودقيقة لتوصيف تطور البنية المجهرية على النطاق الذري.

خوارزميات الديناميات الجزيئية

فحص إمكانات كولوم نموذج المذيب الضمني.

التكامل

تكامل عاطفي.
التكامل بين فيرلت و ستويرمر.
تكامل طريقة رونج-كوتا.
خوارزمية بيمان.
خوارزميات القيد (للأنظمة المقيدة).

خوارزميات التفاعل قصير المدى

قوائم الخلايا.
قائمة فيرلت.
التفاعلات المستعبدة.

خوارزميات التفاعل بعيد المدى

تلخيص ايوالد.
تجميع ايوالد لشبكة الجسيمات (PME).
جسيمات - جسيمات - جسيمات - شبكة (P3M).
طريقة القوة المتغيرة.

استراتيجيات الموازاة

طريقة تحليل المجال (توزيع بيانات النظام للحوسبة المتوازية).

الديناميات الجزيئية لكيمياء الكم

الديناميكيات الجزيئية لسيارة بارينيلو.

أجهزة متخصصة لمحاكاة الديناميكا الجزيئية

أنطون - كمبيوتر عملاق متخصص ومتوازي بشكل كبير مصمم لتنفيذ عمليات محاكاة الديناميكا الجزيئية.
MDGRAPE - نظام ذو غرض خاص مصمم لمحاكاة الديناميكيات الجزيئية، وخاصة التنبؤ ببنية البروتين.

بطاقة الرسومات كأداة لمحاكاة الديناميكا الجزيئية

النمذجة الجزيئية على (GPU).

انظر أيضًا

مراجع

"معلومات عن ديناميكا جزيئية على موقع universalis.fr"، universalis.fr، مؤرشف من الأصل في 25 يوليو 2019.
"معلومات عن ديناميكا جزيئية على موقع britannica.com"، britannica.com، مؤرشف من الأصل في 6 أغسطس 2016.
"معلومات عن ديناميكا جزيئية على موقع dx.doi.org"، dx.doi.org، مؤرشف من الأصل في 2 يونيو 2018.
Schlick, Tamar (1996)، "Pursuing Laplace's Vision on Modern Computers"، Mathematical Approaches to Biomolecular Structure and Dynamics، The IMA Volumes in Mathematics and its Applications، ج. 82، ص. 219–247، doi:10.1007/978-1-4612-4066-2_13، ISBN 978-0-387-94838-6.
Bernal, J. D. (يناير 1997)، "The Bakerian Lecture, 1962 The structure of liquids"، Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences، 280 (1382): 299–322، Bibcode:1964RSPSA.280..299B، doi:10.1098/rspa.1964.0147.
Fermi E., Pasta J., Ulam S., Los Alamos report LA-1940 (1955).
Alder, B. J.؛ Wainwright, T. E. (أغسطس 1959)، "Studies in Molecular Dynamics. I. General Method"، The Journal of Chemical Physics، 31 (2): 459–466، Bibcode:1959JChPh..31..459A، doi:10.1063/1.1730376.
Gibson, J B؛ Goland, A N؛ Milgram, M؛ Vineyard, G H (1960)، "Dynamics of Radiation Damage"، Phys. Rev.، 120 (4): 1229–1253، Bibcode:1960PhRv..120.1229G، doi:10.1103/PhysRev.120.1229.
Rahman, A. (19 أكتوبر 1964)، "Correlations in the Motion of Atoms in Liquid Argon"، Physical Review، 136 (2A): A405–A411، Bibcode:1964PhRv..136..405R، doi:10.1103/PhysRev.136.A405.
Koehl, P.؛ Levitt, Michael (1999)، "A brighter future for protein structure prediction"، Nature Structural Biology، 6 (2): 108–111، doi:10.1038/5794، PMID 10048917.
Raval, A؛ Piana, S؛ Eastwood, MP؛ Dror, RO؛ Shaw, DE (أغسطس 2012)، "Refinement of protein structure homology models via long, all-atom molecular dynamics simulations."، Proteins، 80 (8): 2071–9، doi:10.1002/prot.24098، PMID 22513870.
Beauchamp, KA؛ Lin, YS؛ Das, R؛ Pande, VS (10 أبريل 2012)، "Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements."، Journal of Chemical Theory and Computation، 8 (4): 1409–1414، doi:10.1021/ct2007814، PMID 22754404.
Piana, S؛ Klepeis, JL؛ Shaw, DE (فبراير 2014)، "Assessing the accuracy of physical models used in protein-folding simulations: quantitative evidence from long molecular dynamics simulations"، Current Opinion in Structural Biology، 24: 98–105، doi:10.1016/j.sbi.2013.12.006، PMID 24463371.
Dynamics based pharmacophore models for screening potential inhibitors of mycobacterial cyclopropane synthase Chinmayee Choudhury et al. J Chem Inf Model. 2015.. نسخة محفوظة 2020-10-17 على موقع واي باك مشين.
Molecular dynamics study of peptide segments of the BH3 domain of the proapoptotic proteins Bak, Bax, Bid and Hrk bound to the Bcl-xL and Bcl-2. نسخة محفوظة 2018-06-05 على موقع واي باك مشين.
Combining molecular dynamics simulation and ligand-receptor contacts analysis as a new approach for pharmacophore modeling: beta-secretase 1 and check point kinase 1 as case studies, Ma'mon M Hatmal et al. J Comput Aided Mol Des. 2016 Dec نسخة محفوظة 24 ديسمبر 2021 على موقع واي باك مشين.
Hydrophobic effects are mostly of entropic nature at room temperature.
Myers, J. K.؛ Pace, C. N. (1996)، "Hydrogen bonding stabilizes globular proteins"، Biophys. J.، 71 (4): 2033–2039، Bibcode:1996BpJ....71.2033M، doi:10.1016/s0006-3495(96)79401-8، PMID 8889177.
Israelachvili, Jacob (1992). Intermolecular and surface forces. Academic Press, San Diego.
Cruz, F.J.A.L.؛ de Pablo, J.J.؛ Mota, J.P.B. (2014)، "Endohedral confinement of a DNA dodecamer onto pristine carbon nanotubes and the stability of the canonical B form"، J. Chem. Phys.، ج. 140، ص. 225103، arXiv:1605.01317، Bibcode:2014JChPh.140v5103C، doi:10.1063/1.4881422، PMID 24929415
Cruz, F.J.A.L.؛ Mota, J.P.B. (2016)، "Conformational Thermodynamics of DNA Strands in Hydrophilic Nanopores"، J. Phys. Chem. C، ج. 120، ص. 20357–20367، doi:10.1021/acs.jpcc.6b06234
Plimpton, Steve. Molecular Dynamics - Parallel Algorithms. sandia.gov نسخة محفوظة 2018-07-15 على موقع واي باك مشين.
Streett WB, Tildesley DJ, Saville G؛ Tildesley؛ Saville (1978)، "Multiple time-step methods in molecular dynamics"، Mol Phys، 35 (3): 639–648، Bibcode:1978MolPh..35..639S، doi:10.1080/00268977800100471.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
Tuckerman ME, Berne BJ, Martyna GJ؛ Berne؛ Martyna (1991)، "Molecular dynamics algorithm for multiple time scales: systems with long range forces"، J Chem Phys، 94 (10): 6811–6815، Bibcode:1991JChPh..94.6811T، doi:10.1063/1.460259.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
Tuckerman ME, Berne BJ, Martyna GJ؛ Berne؛ Martyna (1992)، "Reversible multiple time scale molecular dynamics"، J Chem Phys، 97 (3): 1990–2001، Bibcode:1992JChPh..97.1990T، doi:10.1063/1.463137.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
Sugita, Yuji؛ Okamoto, Yuko (نوفمبر 1999)، "Replica-exchange molecular dynamics method for protein folding"، Chemical Physics Letters، 314 (1–2): 141–151، Bibcode:1999CPL...314..141S، doi:10.1016/S0009-2614(99)01123-9.
Sinnott, S. B.؛ Brenner, D. W. (2012)، "Three decades of many-body potentials in materials research"، MRS Bulletin، 37 (5): 469–473، doi:10.1557/mrs.2012.88.
Albe, K.؛ Nordlund, K.؛ Averback, R. S. (2002)، "Modeling metal-semiconductor interaction: Analytical bond-order potential for platinum-carbon"، Phys. Rev. B، 65 (19): 195124، Bibcode:2002PhRvB..65s5124A، doi:10.1103/physrevb.65.195124.
Brenner, Donald W. (15 نوفمبر 1990)، "Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films"، Physical Review B، 42 (15): 9458–9471، Bibcode:1990PhRvB..42.9458B، doi:10.1103/physrevb.42.9458، PMID 9995183، مؤرشف من الأصل في 22 سبتمبر 2017.
Beardmore, Keith؛ Smith, Roger (1996)، "Empirical potentials for C-Si-H systems with application to C₆₀ interactions with Si crystal surfaces"، Philosophical Magazine A، 74 (6): 1439–1466، Bibcode:1996PMagA..74.1439B، doi:10.1080/01418619608240734.
Ni, Boris؛ Lee, Ki-Ho؛ Sinnott, Susan B (2004)، "A reactive empirical bond order (rebo) potential for hydrocarbon oxygen interactions"، Journal of Physics: Condensed Matter، 16 (41): 7261–7275، Bibcode:2004JPCM...16.7261N، doi:10.1088/0953-8984/16/41/008.
van Duin, Adri C. T.؛ Dasgupta, Siddharth؛ Lorant, Francois؛ Goddard, William A. (أكتوبر 2001)، "ReaxFF: A Reactive Force Field for Hydrocarbons"، The Journal of Physical Chemistry A، 105 (41): 9396–9409، Bibcode:2001JPCA..105.9396V، doi:10.1021/jp004368u.
Cruz, Fernando J. A. L.؛ Canongia Lopes, José N.؛ Calado, Jorge C. G.؛ Minas da Piedade, Manuel E. (ديسمبر 2005)، "A Molecular Dynamics Study of the Thermodynamic Properties of Calcium Apatites. 1. Hexagonal Phases"، The Journal of Physical Chemistry B، 109 (51): 24473–24479، doi:10.1021/jp054304p، PMID 16375450.
Cruz, Fernando J.A.L.؛ Lopes, José N. Canongia؛ Calado, Jorge C.G. (مارس 2006)، "Molecular dynamics simulations of molten calcium hydroxyapatite"، Fluid Phase Equilibria، 241 (1–2): 51–58، doi:10.1016/j.fluid.2005.12.021.
Justo, J. F.؛ Bazant, M. Z.؛ Kaxiras, E.؛ Bulatov, V. V.؛ Yip, S. (1998)، "Interatomic potential for silicon defects and disordered phases"، Phys. Rev. B، 58 (5): 2539–2550، arXiv:cond-mat/9712058، Bibcode:1998PhRvB..58.2539J، doi:10.1103/PhysRevB.58.2539.
Tersoff, J. (15 مارس 1989)، "Modeling solid-state chemistry: Interatomic potentials for multicomponent systems"، Physical Review B، 39 (8): 5566–5568، Bibcode:1989PhRvB..39.5566T، doi:10.1103/physrevb.39.5566، PMID 9948964.
Daw, Murray S.؛ Foiles, Stephen M.؛ Baskes, Michael I. (مارس 1993)، "The embedded-atom method: a review of theory and applications"، Materials Science Reports، 9 (7–8): 251–310، doi:10.1016/0920-2307(93)90001-U، مؤرشف من الأصل في 30 أكتوبر 2021.
Cleri, Fabrizio؛ Rosato, Vittorio (01 يوليو 1993)، "Tight-binding potentials for transition metals and alloys"، Physical Review B، 48 (1): 22–33، Bibcode:1993PhRvB..48...22C، doi:10.1103/physrevb.48.22، PMID 10006745.
Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD؛ Harder؛ Vorobyov؛ Roux؛ MacKerell (2006)، "A polarizable model of water for molecular dynamics simulations of biomolecules"، Chem Phys Lett، 418 (1): 245–249، Bibcode:2006CPL...418..245L، doi:10.1016/j.cplett.2005.10.135.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
"Signature properties of water: Their molecular electronic origins"، Proceedings of the National Academy of Sciences، 112 (20): 6341–6346، 2015، Bibcode:2015PNAS..112.6341S، doi:10.1073/pnas.1418982112، PMID 25941394.
"Hydrogen bonding and molecular orientation at the liquid–vapour interface of water"، Physical Chemistry Chemical Physics، 17 (14): 8660–8669، 2015، Bibcode:2015PCCP...17.8660C، doi:10.1039/C4CP05506C، PMID 25715668.
Mahmoudi, Morteza؛ Lynch, Iseult؛ Ejtehadi, Mohammad Reza؛ Monopoli, Marco P.؛ Bombelli, Francesca Baldelli؛ Laurent, Sophie (2011)، "Protein−Nanoparticle Interactions: Opportunities and Challenges"، Chemical Reviews، 111 (9): 5610–37، doi:10.1021/cr100440g، PMID 21688848.
Patel, S.؛ MacKerell, Jr. AD؛ Brooks III, Charles L (2004)، "CHARMM fluctuating charge force field for proteins: II protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model"، J Comput Chem، 25 (12): 1504–1514، doi:10.1002/jcc.20077، PMID 15224394.
The methodology for such methods was introduced by Warshel and coworkers. In the recent years have been pioneered by several groups including: أريه وارشيل (جامعة كاليفورنيا الجنوبية), Weitao Yang (جامعة ديوك), Sharon Hammes-Schiffer (جامعة ولاية بنسلفانيا), Donald Truhlar and Jiali Gao (جامعة منيسوتا) and Kenneth Merz (جامعة فلوريدا).
Billeter, Salomon R.؛ Webb, Simon P.؛ Agarwal, Pratul K.؛ Iordanov, Tzvetelin؛ Hammes-Schiffer, Sharon (نوفمبر 2001)، "Hydride Transfer in Liver Alcohol Dehydrogenase: Quantum Dynamics, Kinetic Isotope Effects, and Role of Enzyme Motion"، Journal of the American Chemical Society، 123 (45): 11262–11272، doi:10.1021/ja011384b، PMID 11697969.
Kmiecik, Sebastian؛ Gront, Dominik؛ Kolinski, Michal؛ Wieteska, Lukasz؛ Dawid, Aleksandra Elzbieta؛ Kolinski, Andrzej (22 يونيو 2016)، "Coarse-Grained Protein Models and Their Applications"، Chemical Reviews، 116 (14): 7898–7936، doi:10.1021/acs.chemrev.6b00163، PMID 27333362.
Voegler Smith, Anne؛ Hall, Carol K. (15 أغسطس 2001)، "?-Helix formation: Discontinuous molecular dynamics on an intermediate-resolution protein model"، Proteins: Structure, Function, and Genetics، 44 (3): 344–360، doi:10.1002/prot.1100، PMID 11455608.
Ding, F؛ Borreguero, JM؛ Buldyrey, SV؛ Stanley, HE؛ Dokholyan, NV (01 نوفمبر 2003)، "Mechanism for the alpha-helix to beta-hairpin transition"، Proteins، 53 (2): 220–8، doi:10.1002/prot.10468، PMID 14517973.
Paci, Emanuele؛ Vendruscolo, Michele؛ Karplus, Martin (ديسمبر 2002)، "Validity of Gō Models: Comparison with a Solvent-Shielded Empirical Energy Decomposition"، Biophysical Journal، 83 (6): 3032–3038، Bibcode:2002BpJ....83.3032P، doi:10.1016/S0006-3495(02)75308-3، PMID 12496075.
Chakrabarty, Arnab؛ Cagin, Tahir (مايو 2010)، "Coarse grain modeling of polyimide copolymers"، Polymer، 51 (12): 2786–2794، doi:10.1016/j.polymer.2010.03.060.
Foley, Thomas T.؛ Shell, M. Scott؛ Noid, W. G. (02 سبتمبر 2015)، "The impact of resolution upon entropy and information in coarse-grained models"، The Journal of Chemical Physics، 143 (24): 243104، doi:10.1063/1.4929836، ISSN 0021-9606، PMID 26723589، مؤرشف من الأصل في 24 ديسمبر 2021.
Heydari, Tiam؛ Heidari, Maziar؛ Mashinchian, Omid؛ Wojcik, Michal؛ Xu, Ke؛ Dalby, Matthew John؛ Mahmoudi, Morteza؛ Ejtehadi, Mohammad Reza (2017)، "Development of a Virtual Cell Model to Predict Cell Response to Substrate Topography"، ACS Nano، 11 (9): 9084–9092، doi:10.1021/acsnano.7b03732، PMID 28742318.
Leach, Dr Andrew (30 يناير 2001)، Molecular Modelling: Principles and Applications (باللغة الإنجليزية) (ط. 2nd)، Harlow: Prentice Hall، ISBN 9780582382107، (أمازون 0582382106).
Allen, Michael P.؛ Tildesley, Dominic J. (22 أغسطس 2017)، Computer Simulation of Liquids (باللغة الإنجليزية) (ط. 2nd)، Oxford University Press، ص. 216، ISBN 9780198803201، (أمازون 0198803206).
Nienhaus, Gerd Ulrich (2005)، Protein-ligand interactions: methods and applications، ص. 54–56، ISBN 978-1-61737-525-5.
Leszczyński, Jerzy (2005)، Computational chemistry: reviews of current trends, Volume 9، ص. 54–56، ISBN 978-981-256-742-0.
Kumar, Shankar؛ Rosenberg, John M.؛ Bouzida, Djamal؛ Swendsen, Robert H.؛ Kollman, Peter A. (أكتوبر 1992)، "The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method"، Journal of Computational Chemistry، 13 (8): 1011–1021، doi:10.1002/jcc.540130812.
Bartels, Christian (ديسمبر 2000)، "Analyzing biased Monte Carlo and molecular dynamics simulations"، Chemical Physics Letters، 331 (5–6): 446–454، Bibcode:2000CPL...331..446B، doi:10.1016/S0009-2614(00)01215-X.
Lemkul, Justin A.؛ Bevan, David R. (04 فبراير 2010)، "Assessing the Stability of Alzheimer's Amyloid Protofibrils Using Molecular Dynamics"، The Journal of Physical Chemistry B، 114 (4): 1652–1660، doi:10.1021/jp9110794، PMID 20055378.
Patel, Jagdish Suresh؛ Berteotti, Anna؛ Ronsisvalle, Simone؛ Rocchia, Walter؛ Cavalli, Andrea (28 يناير 2014)، "Steered Molecular Dynamics Simulations for Studying Protein–Ligand Interaction in Cyclin-Dependent Kinase 5"، Journal of Chemical Information and Modeling، 54 (2): 470–480، doi:10.1021/ci4003574، PMID 24437446.
Gosai, Agnivo؛ Ma, Xiao؛ Balasubramanian, Ganesh؛ Shrotriya, Pranav (22 نوفمبر 2016)، "Electrical Stimulus Controlled Binding/Unbinding of Human Thrombin-Aptamer Complex"، Scientific Reports، 6 (1): 37449، Bibcode:2016NatSR...637449G، doi:10.1038/srep37449، PMID 27874042.
Levitt, Michael؛ Warshel, Arieh (01 فبراير 1975)، "Computer simulation of protein folding"، Nature، 253 (5494): 694–698، Bibcode:1975Natur.253..694L، doi:10.1038/253694a0، PMID 1167625.
Warshel, Arieh (أبريل 1976)، "Bicycle-pedal model for the first step in the vision process"، Nature، 260 (5553): 679–683، Bibcode:1976Natur.260..679W، doi:10.1038/260679a0، PMID 1264239.
Smith, R., المحرر (1997)، Atomic & ion collisions in solids and at surfaces: theory, simulation and applications، Cambridge, UK: Cambridge University Press.^{[بحاجة لرقم الصفحة]}
"Molecular dynamics simulation of the Satellite Tobacco Mosaic Virus (STMV)"، Theoretical and Computational Biophysics Group، University of Illinois at Urbana Champaign، مؤرشف من الأصل في 21 أكتوبر 2021.
Jayachandran, Guha؛ Vishal, V.؛ Pande, Vijay S. (28 أبريل 2006)، "Using massively parallel simulation and Markovian models to study protein folding: Examining the dynamics of the villin headpiece"، The Journal of Chemical Physics، 124 (16): 164902، Bibcode:2006JChPh.124p4902J، doi:10.1063/1.2186317، PMID 16674165.
Lindorff-Larsen, Kresten؛ Piana, Stefano؛ Dror, Ron O.؛ Shaw, David E. (2011)، "How Fast-Folding Proteins Fold"، Science، 334 (6055): 517–520، Bibcode:2011Sci...334..517L، doi:10.1126/science.1208351، PMID 22034434.
Shaw, David E.؛ Maragakis, Paul؛ Lindorff-Larsen, Kresten؛ Piana, Stefano؛ Dror, Ron O.؛ Eastwood, Michael P.؛ Bank, Joseph A.؛ Jumper, John M.؛ Salmon, John K.؛ وآخرون (2010)، "Atomic-Level Characterization of the Structural Dynamics of Proteins"، Science، 330 (6002): 341–346، Bibcode:2010Sci...330..341S، doi:10.1126/science.1187409، PMID 20947758.

مراجع عامة

M. P. Allen, D. J. Tildesley (1989) Computer simulation of liquids. Oxford University Press. (ردمك 0-19-855645-4).
J. A. McCammon, S. C. Harvey (1987) Dynamics of Proteins and Nucleic Acids. Cambridge University Press. (ردمك 0-521-30750-3) (hardback).
D. C. Rapaport (1996) The Art of Molecular Dynamics Simulation. (ردمك 0-521-44561-2).
M. Griebel؛ S. Knapek؛ G. Zumbusch (2007)، Numerical Simulation in Molecular Dynamics، Berlin, Heidelberg: Springer، ISBN 978-3-540-68094-9.
Frenkel, Daan؛ Smit, Berend (2002) [2001]، Understanding Molecular Simulation : from algorithms to applications، San Diego: Academic Press، ISBN 978-0-12-267351-1.
J. M. Haile (2001) Molecular Dynamics Simulation: Elementary Methods. (ردمك 0-471-18439-X)
R. J. Sadus, Molecular Simulation of Fluids: Theory, Algorithms and Object-Orientation, 2002, (ردمك 0-444-51082-6)
Oren M. Becker, Alexander D. Mackerell, Jr., Benoît Roux, Masakatsu Watanabe (2001) Computational Biochemistry and Biophysics. Marcel Dekker. (ردمك 0-8247-0455-X).
Andrew Leach (2001) Molecular Modelling: Principles and Applications. (2nd Edition) Prentice Hall. (ردمك 978-0-582-38210-7).
Tamar Schlick (2002) Molecular Modeling and Simulation. Springer. (ردمك 0-387-95404-X).
William Graham Hoover (1991) Computational Statistical Mechanics, Elsevier, (ردمك 0-444-88192-1).
D. J. Evans and G. P. Morriss (2008) Statistical Mechanics of Nonequilibrium Liquids, Second Edition, Cambridge University Press, (ردمك 978-0-521-85791-8).

بوابة كيمياء فيزيائية
بوابة الفيزياء
بوابة الكيمياء

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "معلومات عن ديناميكا جزيئية على موقع universalis.fr"، universalis.fr، مؤرشف من الأصل في 25 يوليو 2019.

[2] "معلومات عن ديناميكا جزيئية على موقع britannica.com"، britannica.com، مؤرشف من الأصل في 6 أغسطس 2016.

[3] "معلومات عن ديناميكا جزيئية على موقع dx.doi.org"، dx.doi.org، مؤرشف من الأصل في 2 يونيو 2018.

[4] Schlick, Tamar (1996)، "Pursuing Laplace's Vision on Modern Computers"، Mathematical Approaches to Biomolecular Structure and Dynamics، The IMA Volumes in Mathematics and its Applications، ج. 82، ص. 219–247، doi:10.1007/978-1-4612-4066-2_13، ISBN 978-0-387-94838-6.

[5] Bernal, J. D. (يناير 1997)، "The Bakerian Lecture, 1962 The structure of liquids"، Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences، 280 (1382): 299–322، Bibcode:1964RSPSA.280..299B، doi:10.1098/rspa.1964.0147.

[fput-6] Fermi E., Pasta J., Ulam S., Los Alamos report LA-1940 (1955).

[a&w-7] Alder, B. J.؛ Wainwright, T. E. (أغسطس 1959)، "Studies in Molecular Dynamics. I. General Method"، The Journal of Chemical Physics، 31 (2): 459–466، Bibcode:1959JChPh..31..459A، doi:10.1063/1.1730376.

[8] Gibson, J B؛ Goland, A N؛ Milgram, M؛ Vineyard, G H (1960)، "Dynamics of Radiation Damage"، Phys. Rev.، 120 (4): 1229–1253، Bibcode:1960PhRv..120.1229G، doi:10.1103/PhysRev.120.1229.

[a.rahman-9] Rahman, A. (19 أكتوبر 1964)، "Correlations in the Motion of Atoms in Liquid Argon"، Physical Review، 136 (2A): A405–A411، Bibcode:1964PhRv..136..405R، doi:10.1103/PhysRev.136.A405.

[Koehl-10] Koehl, P.؛ Levitt, Michael (1999)، "A brighter future for protein structure prediction"، Nature Structural Biology، 6 (2): 108–111، doi:10.1038/5794، PMID 10048917.

[11] Raval, A؛ Piana, S؛ Eastwood, MP؛ Dror, RO؛ Shaw, DE (أغسطس 2012)، "Refinement of protein structure homology models via long, all-atom molecular dynamics simulations."، Proteins، 80 (8): 2071–9، doi:10.1002/prot.24098، PMID 22513870.

[12] Beauchamp, KA؛ Lin, YS؛ Das, R؛ Pande, VS (10 أبريل 2012)، "Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements."، Journal of Chemical Theory and Computation، 8 (4): 1409–1414، doi:10.1021/ct2007814، PMID 22754404.

[13] Piana, S؛ Klepeis, JL؛ Shaw, DE (فبراير 2014)، "Assessing the accuracy of physical models used in protein-folding simulations: quantitative evidence from long molecular dynamics simulations"، Current Opinion in Structural Biology، 24: 98–105، doi:10.1016/j.sbi.2013.12.006، PMID 24463371.

[14] Dynamics based pharmacophore models for screening potential inhibitors of mycobacterial cyclopropane synthase Chinmayee Choudhury et al. J Chem Inf Model. 2015.. نسخة محفوظة 2020-10-17 على موقع واي باك مشين.

[15] Molecular dynamics study of peptide segments of the BH3 domain of the proapoptotic proteins Bak, Bax, Bid and Hrk bound to the Bcl-xL and Bcl-2. نسخة محفوظة 2018-06-05 على موقع واي باك مشين.

[16] Combining molecular dynamics simulation and ligand-receptor contacts analysis as a new approach for pharmacophore modeling: beta-secretase 1 and check point kinase 1 as case studies, Ma'mon M Hatmal et al. J Comput Aided Mol Des. 2016 Dec نسخة محفوظة 24 ديسمبر 2021 على موقع واي باك مشين.

[17] Hydrophobic effects are mostly of entropic nature at room temperature.

[Myers-18] Myers, J. K.؛ Pace, C. N. (1996)، "Hydrogen bonding stabilizes globular proteins"، Biophys. J.، 71 (4): 2033–2039، Bibcode:1996BpJ....71.2033M، doi:10.1016/s0006-3495(96)79401-8، PMID 8889177.

[Israelachvili-19] Israelachvili, Jacob (1992). Intermolecular and surface forces. Academic Press, San Diego.

[ReferenceB-20] Cruz, F.J.A.L.؛ de Pablo, J.J.؛ Mota, J.P.B. (2014)، "Endohedral confinement of a DNA dodecamer onto pristine carbon nanotubes and the stability of the canonical B form"، J. Chem. Phys.، ج. 140، ص. 225103، arXiv:1605.01317، Bibcode:2014JChPh.140v5103C، doi:10.1063/1.4881422، PMID 24929415

[ReferenceC-21] Cruz, F.J.A.L.؛ Mota, J.P.B. (2016)، "Conformational Thermodynamics of DNA Strands in Hydrophilic Nanopores"، J. Phys. Chem. C، ج. 120، ص. 20357–20367، doi:10.1021/acs.jpcc.6b06234

[22] Plimpton, Steve. Molecular Dynamics - Parallel Algorithms. sandia.gov نسخة محفوظة 2018-07-15 على موقع واي باك مشين.

[Streett-23] Streett WB, Tildesley DJ, Saville G؛ Tildesley؛ Saville (1978)، "Multiple time-step methods in molecular dynamics"، Mol Phys، 35 (3): 639–648، Bibcode:1978MolPh..35..639S، doi:10.1080/00268977800100471.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

[Tuckerman1991-24] Tuckerman ME, Berne BJ, Martyna GJ؛ Berne؛ Martyna (1991)، "Molecular dynamics algorithm for multiple time scales: systems with long range forces"، J Chem Phys، 94 (10): 6811–6815، Bibcode:1991JChPh..94.6811T، doi:10.1063/1.460259.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

[Tuckerman1992-25] Tuckerman ME, Berne BJ, Martyna GJ؛ Berne؛ Martyna (1992)، "Reversible multiple time scale molecular dynamics"، J Chem Phys، 97 (3): 1990–2001، Bibcode:1992JChPh..97.1990T، doi:10.1063/1.463137.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

[26] Sugita, Yuji؛ Okamoto, Yuko (نوفمبر 1999)، "Replica-exchange molecular dynamics method for protein folding"، Chemical Physics Letters، 314 (1–2): 141–151، Bibcode:1999CPL...314..141S، doi:10.1016/S0009-2614(99)01123-9.

[27] Sinnott, S. B.؛ Brenner, D. W. (2012)، "Three decades of many-body potentials in materials research"، MRS Bulletin، 37 (5): 469–473، doi:10.1557/mrs.2012.88.

[28] Albe, K.؛ Nordlund, K.؛ Averback, R. S. (2002)، "Modeling metal-semiconductor interaction: Analytical bond-order potential for platinum-carbon"، Phys. Rev. B، 65 (19): 195124، Bibcode:2002PhRvB..65s5124A، doi:10.1103/physrevb.65.195124.

[29] Brenner, Donald W. (15 نوفمبر 1990)، "Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films"، Physical Review B، 42 (15): 9458–9471، Bibcode:1990PhRvB..42.9458B، doi:10.1103/physrevb.42.9458، PMID 9995183، مؤرشف من الأصل في 22 سبتمبر 2017.

[30] Beardmore, Keith؛ Smith, Roger (1996)، "Empirical potentials for C-Si-H systems with application to C₆₀ interactions with Si crystal surfaces"، Philosophical Magazine A، 74 (6): 1439–1466، Bibcode:1996PMagA..74.1439B، doi:10.1080/01418619608240734.

[31] Ni, Boris؛ Lee, Ki-Ho؛ Sinnott, Susan B (2004)، "A reactive empirical bond order (rebo) potential for hydrocarbon oxygen interactions"، Journal of Physics: Condensed Matter، 16 (41): 7261–7275، Bibcode:2004JPCM...16.7261N، doi:10.1088/0953-8984/16/41/008.

[32] van Duin, Adri C. T.؛ Dasgupta, Siddharth؛ Lorant, Francois؛ Goddard, William A. (أكتوبر 2001)، "ReaxFF: A Reactive Force Field for Hydrocarbons"، The Journal of Physical Chemistry A، 105 (41): 9396–9409، Bibcode:2001JPCA..105.9396V، doi:10.1021/jp004368u.

[33] Cruz, Fernando J. A. L.؛ Canongia Lopes, José N.؛ Calado, Jorge C. G.؛ Minas da Piedade, Manuel E. (ديسمبر 2005)، "A Molecular Dynamics Study of the Thermodynamic Properties of Calcium Apatites. 1. Hexagonal Phases"، The Journal of Physical Chemistry B، 109 (51): 24473–24479، doi:10.1021/jp054304p، PMID 16375450.

[34] Cruz, Fernando J.A.L.؛ Lopes, José N. Canongia؛ Calado, Jorge C.G. (مارس 2006)، "Molecular dynamics simulations of molten calcium hydroxyapatite"، Fluid Phase Equilibria، 241 (1–2): 51–58، doi:10.1016/j.fluid.2005.12.021.

[ReferenceA-35] Justo, J. F.؛ Bazant, M. Z.؛ Kaxiras, E.؛ Bulatov, V. V.؛ Yip, S. (1998)، "Interatomic potential for silicon defects and disordered phases"، Phys. Rev. B، 58 (5): 2539–2550، arXiv:cond-mat/9712058، Bibcode:1998PhRvB..58.2539J، doi:10.1103/PhysRevB.58.2539.

[36] Tersoff, J. (15 مارس 1989)، "Modeling solid-state chemistry: Interatomic potentials for multicomponent systems"، Physical Review B، 39 (8): 5566–5568، Bibcode:1989PhRvB..39.5566T، doi:10.1103/physrevb.39.5566، PMID 9948964.

[37] Daw, Murray S.؛ Foiles, Stephen M.؛ Baskes, Michael I. (مارس 1993)، "The embedded-atom method: a review of theory and applications"، Materials Science Reports، 9 (7–8): 251–310، doi:10.1016/0920-2307(93)90001-U، مؤرشف من الأصل في 30 أكتوبر 2021.

[38] Cleri, Fabrizio؛ Rosato, Vittorio (01 يوليو 1993)، "Tight-binding potentials for transition metals and alloys"، Physical Review B، 48 (1): 22–33، Bibcode:1993PhRvB..48...22C، doi:10.1103/physrevb.48.22، PMID 10006745.

[Lamoureux3-39] Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD؛ Harder؛ Vorobyov؛ Roux؛ MacKerell (2006)، "A polarizable model of water for molecular dynamics simulations of biomolecules"، Chem Phys Lett، 418 (1): 245–249، Bibcode:2006CPL...418..245L، doi:10.1016/j.cplett.2005.10.135.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

[Sokhan2015-40] "Signature properties of water: Their molecular electronic origins"، Proceedings of the National Academy of Sciences، 112 (20): 6341–6346، 2015، Bibcode:2015PNAS..112.6341S، doi:10.1073/pnas.1418982112، PMID 25941394.

[Cipcigan-41] "Hydrogen bonding and molecular orientation at the liquid–vapour interface of water"، Physical Chemistry Chemical Physics، 17 (14): 8660–8669، 2015، Bibcode:2015PCCP...17.8660C، doi:10.1039/C4CP05506C، PMID 25715668.

[42] Mahmoudi, Morteza؛ Lynch, Iseult؛ Ejtehadi, Mohammad Reza؛ Monopoli, Marco P.؛ Bombelli, Francesca Baldelli؛ Laurent, Sophie (2011)، "Protein−Nanoparticle Interactions: Opportunities and Challenges"، Chemical Reviews، 111 (9): 5610–37، doi:10.1021/cr100440g، PMID 21688848.

[Patel2004b-43] Patel, S.؛ MacKerell, Jr. AD؛ Brooks III, Charles L (2004)، "CHARMM fluctuating charge force field for proteins: II protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model"، J Comput Chem، 25 (12): 1504–1514، doi:10.1002/jcc.20077، PMID 15224394.

[44] The methodology for such methods was introduced by Warshel and coworkers. In the recent years have been pioneered by several groups including: أريه وارشيل (جامعة كاليفورنيا الجنوبية), Weitao Yang (جامعة ديوك), Sharon Hammes-Schiffer (جامعة ولاية بنسلفانيا), Donald Truhlar and Jiali Gao (جامعة منيسوتا) and Kenneth Merz (جامعة فلوريدا).

[45] Billeter, Salomon R.؛ Webb, Simon P.؛ Agarwal, Pratul K.؛ Iordanov, Tzvetelin؛ Hammes-Schiffer, Sharon (نوفمبر 2001)، "Hydride Transfer in Liver Alcohol Dehydrogenase: Quantum Dynamics, Kinetic Isotope Effects, and Role of Enzyme Motion"، Journal of the American Chemical Society، 123 (45): 11262–11272، doi:10.1021/ja011384b، PMID 11697969.

[:0-46] Kmiecik, Sebastian؛ Gront, Dominik؛ Kolinski, Michal؛ Wieteska, Lukasz؛ Dawid, Aleksandra Elzbieta؛ Kolinski, Andrzej (22 يونيو 2016)، "Coarse-Grained Protein Models and Their Applications"، Chemical Reviews، 116 (14): 7898–7936، doi:10.1021/acs.chemrev.6b00163، PMID 27333362.

[47] Voegler Smith, Anne؛ Hall, Carol K. (15 أغسطس 2001)، "?-Helix formation: Discontinuous molecular dynamics on an intermediate-resolution protein model"، Proteins: Structure, Function, and Genetics، 44 (3): 344–360، doi:10.1002/prot.1100، PMID 11455608.

[48] Ding, F؛ Borreguero, JM؛ Buldyrey, SV؛ Stanley, HE؛ Dokholyan, NV (01 نوفمبر 2003)، "Mechanism for the alpha-helix to beta-hairpin transition"، Proteins، 53 (2): 220–8، doi:10.1002/prot.10468، PMID 14517973.

[49] Paci, Emanuele؛ Vendruscolo, Michele؛ Karplus, Martin (ديسمبر 2002)، "Validity of Gō Models: Comparison with a Solvent-Shielded Empirical Energy Decomposition"، Biophysical Journal، 83 (6): 3032–3038، Bibcode:2002BpJ....83.3032P، doi:10.1016/S0006-3495(02)75308-3، PMID 12496075.

[50] Chakrabarty, Arnab؛ Cagin, Tahir (مايو 2010)، "Coarse grain modeling of polyimide copolymers"، Polymer، 51 (12): 2786–2794، doi:10.1016/j.polymer.2010.03.060.

[51] Foley, Thomas T.؛ Shell, M. Scott؛ Noid, W. G. (02 سبتمبر 2015)، "The impact of resolution upon entropy and information in coarse-grained models"، The Journal of Chemical Physics، 143 (24): 243104، doi:10.1063/1.4929836، ISSN 0021-9606، PMID 26723589، مؤرشف من الأصل في 24 ديسمبر 2021.

[52] Heydari, Tiam؛ Heidari, Maziar؛ Mashinchian, Omid؛ Wojcik, Michal؛ Xu, Ke؛ Dalby, Matthew John؛ Mahmoudi, Morteza؛ Ejtehadi, Mohammad Reza (2017)، "Development of a Virtual Cell Model to Predict Cell Response to Substrate Topography"، ACS Nano، 11 (9): 9084–9092، doi:10.1021/acsnano.7b03732، PMID 28742318.

[53] Leach, Dr Andrew (30 يناير 2001)، Molecular Modelling: Principles and Applications (باللغة الإنجليزية) (ط. 2nd)، Harlow: Prentice Hall، ISBN 9780582382107، (أمازون 0582382106).

[54] Allen, Michael P.؛ Tildesley, Dominic J. (22 أغسطس 2017)، Computer Simulation of Liquids (باللغة الإنجليزية) (ط. 2nd)، Oxford University Press، ص. 216، ISBN 9780198803201، (أمازون 0198803206).

[Nienhaus-55] Nienhaus, Gerd Ulrich (2005)، Protein-ligand interactions: methods and applications، ص. 54–56، ISBN 978-1-61737-525-5.

[Leszczyński-56] Leszczyński, Jerzy (2005)، Computational chemistry: reviews of current trends, Volume 9، ص. 54–56، ISBN 978-981-256-742-0.

[57] Kumar, Shankar؛ Rosenberg, John M.؛ Bouzida, Djamal؛ Swendsen, Robert H.؛ Kollman, Peter A. (أكتوبر 1992)، "The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method"، Journal of Computational Chemistry، 13 (8): 1011–1021، doi:10.1002/jcc.540130812.

[58] Bartels, Christian (ديسمبر 2000)، "Analyzing biased Monte Carlo and molecular dynamics simulations"، Chemical Physics Letters، 331 (5–6): 446–454، Bibcode:2000CPL...331..446B، doi:10.1016/S0009-2614(00)01215-X.

[59] Lemkul, Justin A.؛ Bevan, David R. (04 فبراير 2010)، "Assessing the Stability of Alzheimer's Amyloid Protofibrils Using Molecular Dynamics"، The Journal of Physical Chemistry B، 114 (4): 1652–1660، doi:10.1021/jp9110794، PMID 20055378.

[60] Patel, Jagdish Suresh؛ Berteotti, Anna؛ Ronsisvalle, Simone؛ Rocchia, Walter؛ Cavalli, Andrea (28 يناير 2014)، "Steered Molecular Dynamics Simulations for Studying Protein–Ligand Interaction in Cyclin-Dependent Kinase 5"، Journal of Chemical Information and Modeling، 54 (2): 470–480، doi:10.1021/ci4003574، PMID 24437446.

[61] Gosai, Agnivo؛ Ma, Xiao؛ Balasubramanian, Ganesh؛ Shrotriya, Pranav (22 نوفمبر 2016)، "Electrical Stimulus Controlled Binding/Unbinding of Human Thrombin-Aptamer Complex"، Scientific Reports، 6 (1): 37449، Bibcode:2016NatSR...637449G، doi:10.1038/srep37449، PMID 27874042.

[62] Levitt, Michael؛ Warshel, Arieh (01 فبراير 1975)، "Computer simulation of protein folding"، Nature، 253 (5494): 694–698، Bibcode:1975Natur.253..694L، doi:10.1038/253694a0، PMID 1167625.

[63] Warshel, Arieh (أبريل 1976)، "Bicycle-pedal model for the first step in the vision process"، Nature، 260 (5553): 679–683، Bibcode:1976Natur.260..679W، doi:10.1038/260679a0، PMID 1264239.

[Smith-64] Smith, R., المحرر (1997)، Atomic & ion collisions in solids and at surfaces: theory, simulation and applications، Cambridge, UK: Cambridge University Press.^{[بحاجة لرقم الصفحة]}

[65] "Molecular dynamics simulation of the Satellite Tobacco Mosaic Virus (STMV)"، Theoretical and Computational Biophysics Group، University of Illinois at Urbana Champaign، مؤرشف من الأصل في 21 أكتوبر 2021.

[66] Jayachandran, Guha؛ Vishal, V.؛ Pande, Vijay S. (28 أبريل 2006)، "Using massively parallel simulation and Markovian models to study protein folding: Examining the dynamics of the villin headpiece"، The Journal of Chemical Physics، 124 (16): 164902، Bibcode:2006JChPh.124p4902J، doi:10.1063/1.2186317، PMID 16674165.

[DESRES-Science2011-67] Lindorff-Larsen, Kresten؛ Piana, Stefano؛ Dror, Ron O.؛ Shaw, David E. (2011)، "How Fast-Folding Proteins Fold"، Science، 334 (6055): 517–520، Bibcode:2011Sci...334..517L، doi:10.1126/science.1208351، PMID 22034434.

[68] Shaw, David E.؛ Maragakis, Paul؛ Lindorff-Larsen, Kresten؛ Piana, Stefano؛ Dror, Ron O.؛ Eastwood, Michael P.؛ Bank, Joseph A.؛ Jumper, John M.؛ Salmon, John K.؛ وآخرون (2010)، "Atomic-Level Characterization of the Structural Dynamics of Proteins"، Science، 330 (6002): 341–346، Bibcode:2010Sci...330..341S، doi:10.1126/science.1187409، PMID 20947758.