Carré (algèbre)
En arithmétique et en algèbre, le carré est une opération consistant à multiplier un élément par lui-même. La notion s’applique d’abord aux nombres, et en particulier aux entiers naturels, pour lesquels le carré est figuré par une disposition en carré au sens géométrique du terme. Un nombre qui peut s’écrire comme le carré d’un entier est appelé carré parfait. Mais plus généralement, on parle du carré d’une fonction, d’une matrice, ou de tout type d’objet mathématique pour lequel il existe une opération notée multiplicativement, comme la composition des endomorphismes ou le produit cartésien.
Pour les articles homonymes, voir Carré (homonymie).
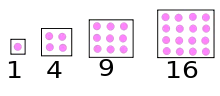
Cette opération apparait dans les identités remarquables, permet de définir la fonction carré et les équations du second degré, et intervient de façon fondamentale dans le théorème de Pythagore et de nombreux autres résultats de toutes les branches des mathématiques. En algèbre géométrique, elle définit la mesure de l’aire d'un carré en fonction de la longueur de son côté.
En informatique, le calcul du carré permet de simplifier le calculs des autres puissances par exponentiation rapide.
En physique, le carré apparait dans de nombreuses formules comme pour la cinétique de la chute libre ou la relation d’Einstein E = mc².
Opération numérique
Notation et premiers exemples
Le carré est défini pour tout nombre n comme le résultat de la multiplication de ce nombre par lui-même, et on le note avec un chiffre 2 en exposant : n2 = n × n.
Les carrés des premiers entiers naturels, appelés carrés parfaits ou nombres carrés, apparaissent sur la diagonale principale de la table de multiplication.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Le carré d’un nombre a la même valeur que le carré de son opposé en vertu de la règle des signes. Mais les conventions sur l’ordre de priorité des opérations font qu’un signe moins (−) (associé par exemple à la notation d’un entier relatif) ne sera pas pris en compte dans le carré en l’absence de parenthèses. De la même manière, toute expression composée avec au moins un opérateur (somme, produit, fraction…) doit être encadrée par des délimiteurs (parenthèses ou crochets) avant d’être notée au carré.
Règles de calcul
Pour une somme ou une différence de deux nombres, le carré peut se calculer en appliquant les premières identités remarquables :
- .
La troisième identité remarquable permet de factoriser une différence de deux carrés :
- .
Le carré d’une fraction est obtenu en calculant le quotient du carré du numérateur par le carré du dénominateur. Cette propriété est parfois transportée de façon erronée dans le calcul du carré des nombres décimaux.
L’identité de Brahmagupta permet d’exprimer le produit de deux sommes de deux carrés comme une somme de deux carrés : quels que soient les nombres a, b, c, d,
- (a2 + b2)(c2 + d2) = (ac − bd)2 + (ad + bc)2.
Inégalités
Tout entier naturel n est inférieur à son carré : n ≤ n2, avec une inégalité stricte dès que n ≥ 2.
le carré est strictement inférieur
Cette inégalité est encore valable pour tous les nombres réels supérieurs à 1, ainsi que pour tous les négatifs, mais elle est fausse pour les réels entre 0 et 1. Ce phénomène se visualise sur la courbe de la fonction carré, qui est au-dessus de la première bissectrice sur ]−∞, 0] ∪ [1, +∞[ mais en dessous sur l’intervalle ]0, 1[.
De même, l’élévation au carré préserve les inégalités entre réels positifs :
mais elle renverse les inégalités entre réels négatifs, et il n’y a pas de règle simple de passage au carré pour une inégalité entre réels quelconques. Ces propriétés correspondent au fait que la fonction carré est croissante sur R+ et décroissante sur R−.
Équation
Une équation de la forme x2 = a, d’inconnue x, n’a de solution réelle que si le paramètre a est positif.
Si a = 0, la seule solution est donnée par x = 0.
Si a > 0, il y a deux solutions réelles opposées définie avec la racine carrée : ou .
Ces solutions ne sont entières que si a est un carré parfait, et ne sont rationnelles que si a est un quotient de carrés parfaits. En particulier, cette propriété implique l’irrationalité de la racine carrée de 2.
Si a < 0, il existe deux solutions complexes qui peuvent s’écrire et . Plus généralement, si a est un nombre complexe s’écrivant sous forme polaire a = r.eiθ, alors l’équation x2 = a a deux solutions complexes opposées et .
Inéquation
Les inéquations de la forme x2 < a, x2 ≤ a, x2 ≥ a, x2 > a peuvent se résoudre à l’aide d’un tableau de signes de la différence x2 − a :
Arithmétique
Dans l’ensemble des entiers naturels
Les carrés parfaits forment une suite infinie de nombres entiers (suite A000290 de l'OEIS) de densité nulle, dont les différences entre termes consécutifs forment la suite des entiers impairs, et dont la série associée est définie par les sommes partielles :
- .
Le carré est utilisé dans certaines équations diophantiennes comme la relation a2 + b2 = c2 des triplets pythagoriciens.
Le théorème des quatre carrés montre que tout entier naturel se décompose en une somme de quatre carrés parfaits.
Le théorème des deux carrés de Fermat donne une condition nécessaire et suffisante pour qu’un entier n se décompose en une somme de deux carrés parfaits, en fonction de la décomposition en facteurs premiers de n.
Arithmétique modulaire
En arithmétique modulaire, si p est un nombre premier impair, l’ensemble des carrés modulo p non nuls forme un sous-groupe d’indice 2 dans le groupe Fp∗ des résidus non nuls modulo p, appelés résidus quadratiques. La détermination du fait qu’un résidu r constitue un carré modulo p se formule avec le symbole de Legendre : . La détermination des résidus quadratiques modulo un entier naturel n quelconque repose sur le symbole de Jacobi.
La recherche des solutions d’une équation x2 ≡ 1 modulo un entier n est équivalente à la décomposition en facteurs premiers de n.
Autres domaines
Ensemble de couples
Étant donné un ensemble E, son carré E2 = E × E est l’ensemble des couples d’éléments de E. Si E est fini, son cardinal s’écrit card(E2) = (card(E))2. En particulier, pour un graphe avec un grand nombre de sommets n, l’ensemble des arêtes est décrit par une partie d’un ensemble de n2 éléments. Par exemple, si chaque sommet représente un site internet, comme il y a plus d’un milliard en 2021[1]), les liens entre eux peuvent être représentés par une matrice de plus d’un milliard de milliards d’éléments.
La notation R2 désigne le plan euclidien muni d’un repère orthonormé par assimilation des points avec leur couples de coordonnées cartésiennes en géométrie analytique.
Algèbre linéaire
Pour une endomorphisme u sur un espace vectoriel E, le carré représente en général son itéré, c’est-à-dire la composée u2 = u ∘ u de l’endomorphisme avec lui-même. Si l’endomorphisme est représenté par une matrice carrée M, son carré u2 est représenté par M2.
Un projecteur est un endomorphisme p idempotent, c’est-à-dire satisfaisant la relation p2 = p. Un symétrie vectorielle est un endomorphisme s involutif, c’est-à-dire satisfaisant la relation s2 = id.
La résolution d’une équation de la forme u2 = v dans l’ensemble des matrices carrées peut être facilitée si l’endomorphisme v est diagonalisable. Dans ce cas, les espaces propres de v sont stables par u, et si les valeurs propres sont des carrés, chaque solution est définie par une famille de symétries vectorielles sur ces sous-espaces.
Probabilités et statistique
L’espérance du carré d’une variable aléatoire réelle X est son second moment m2 = E(X2). Sa variance est égale d’après la formule de Koenig-Huygens à la différence entre l’espérance du carré et le carré de l’espérance : V(X) = E(X2) − (E(X))2, et définit alors le carré de l’écart type.
Caractère
En Unicode, le caractère est U+00B2 ² exposant deux (HTML : ² ²).
Notes et références
- 1 197 982 359 sites selon Web Server Survey le 12 février 2021.
Source principale de cet article : cours de mathématiques niveau 3e / 2de
Voir aussi
- Fonction carré
- Puissance
- Racine carrée
- Théorème des deux carrés
- Théorème des quatre carrés
- Loi de réciprocité quadratique
- Polynôme somme de carrés
- Portail de l’algèbre