Éléments remarquables d'un triangle
Les éléments remarquables d'un triangle sont des points, droites ou cercles définis en relation avec ce triangle et possédant des propriétés géométriques remarquables.
Points remarquables
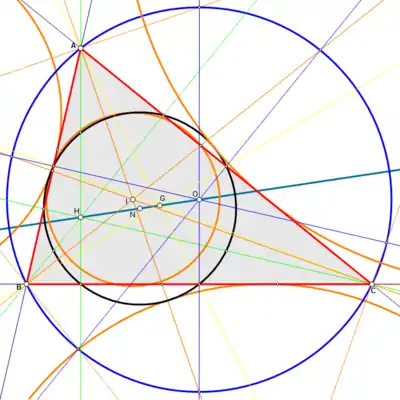
Un triangle scalène ABC avec le centre de gravité G, le centre du cercle inscrit I, le centre du cercle circonscrit O, l'orthocentre H
- Centre de gravité correspondant à l'isobarycentre des sommets et au point de concours des médianes
- Centre du cercle circonscrit ou point de concours des médiatrices
- Centre du cercle inscrit ou point de concours des bissectrices
- Centres des cercles exinscrits
- Orthocentre ou point de concours des hauteurs
- Centre du cercle d'Euler
- Points de Brocard
- Points de Feuerbach
- Point de Fermat ou Point de Torricelli
- Point de Miquel
- Point de Gergonne
- Point de Nagel
- Point de Vecten
- Points isogonaux
- Point de Lemoine
- Points de Terquem
- Point de Spieker
- Point d’Apollonius
- Mittenpunkt
Droites remarquables
Cercles remarquables
Triangles remarquables
Courbes remarquables
- Coniques circonscrites et inscrites à un triangle
- Parabole tritangente
- Ellipse de Mandart
- Ellipse de Steiner
- Ellipse de Brocard
- Ellipse de Lemoine
- Hyperbole de Kiepert
- Parabole de Kiepert
- Conique inscrite de Serret (ou de MacBeath)
- Conique orthique
- cubiques
- Deltoïde de Steiner
Article connexe
Bibliographie
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4)
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.