Convergence de variables aléatoires
Dans la théorie des probabilités, il existe différentes notions de convergence de variables aléatoires. La convergence (dans un des sens décrits ci-dessous) de suites de variables aléatoires est un concept important de la théorie des probabilités utilisé notamment en statistique et dans l'étude des processus stochastiques. Par exemple, la moyenne de n variables aléatoires indépendantes et identiquement distribuées converge presque sûrement vers l'espérance commune de ces variables aléatoires (si celle-ci existe). Ce résultat est connu sous le nom de loi forte des grands nombres.
Dans cet article, on suppose que (Xn) est une suite de variables aléatoires réelles, que X est une variable aléatoire réelle, et que toutes ces variables sont définies sur un même espace probabilisé . D'éventuelles généralisations seront discutées.
Les différents modes de convergence
Il existe plusieurs notions de convergence de variables aléatoires. Elles ont toutes en commun le fait qu'elles sont insensibles face à d'éventuelles modifications négligeables des variables aléatoires. Plus précisément, si converge vers (selon n'importe lequel des sens ci-dessous) et si sont d'autres variables aléatoires telles que pour tout et , alors converge aussi vers .
Convergence essentiellement uniforme (ou L∞)
Rappelons qu'une variable aléatoire réelle est dite essentiellement bornée s'il existe un nombre , appelé borne essentielle, tel que . Dans ce cas on définit comme la borne inférieure de l'ensemble des bornes essentielles de .
Définition (convergence essentiellement uniforme) — On dit que (Xn) converge vers X essentiellement uniformément, ou encore en norme L∞ si, pour tout n, Xn et X sont essentiellement bornées et si
Dans ce cas on note .
Remarques :
- Le fait que et soient essentiellement bornées implique que l'est aussi. Ainsi la quantité est bien définie. Plus précisément l'ensemble des variables aléatoires réelles définies sur essentiellement bornées est un espace vectoriel réel pour lequel la fonction est une semi-norme. Attention ce n'est pas une norme, en général on quotiente par le sous-espace des variables aléatoires presque-sûrement nulles. Sur cet espace quotient, induit une norme.
- Par abus de langage on parle parfois de « convergence uniforme » au lieu de « convergence essentiellement uniforme ». Cependant il ne faut pas s'y tromper, la notion de convergence donnée ci-dessus est plus faible que la convergence uniforme au sens strict. En effet, il se pourrait que les variables soient toutes essentiellement bornées mais non bornées au sens strict auquel cas la convergence uniforme au sens strict n'aurait pas de sens. La raison pour laquelle on considère la convergence essentiellement uniforme plutôt que la convergence uniforme au sens strict et celle donnée plus haut : on veut que la convergence soit insensible face aux modifications négligeables des variables aléatoires. Ce ne serait pas le cas si on prenait la convergence uniforme au sens strict. Donnons un exemple concret : prenons muni de la tribu et de la probabilité définie par et . Prenons les variables définies par , , et pour tout n. Il est clair que ne converge pas uniformément vers au sens strict puisque pour tout n,. En revanche converge essentiellement uniformément vers puisque pour tout n, .
- Si converge essentiellement uniformément vers alors il existe un évènement de probabilité 1 tel que, restreint à , converge uniformément vers au sens strict. Plus précisément, tend vers 0, où est la variable aléatoire qui vaut 1 sur et 0 ailleurs (elle est donc presque-sûrement nulle).
- La convergence essentiellement uniforme se généralise à des variables aléatoires à valeurs dans un espace vectoriel normé muni de sa tribu borélienne. Il est même possible de généraliser cette notion de convergence à des fonctions mesurables sur un espace mesuré.
Convergence en moyenne d'ordre p (ou Lp)
Rappelons qu'une variable aléatoire réelle est dite avoir un moment d'ordre p > 0 fini si . Dans ce cas on définit .
Définition (convergence en moyenne d'ordre p) — Soit p > 0. On dit que (Xn) converge vers X en moyenne d'ordre p ou encore en norme Lp si, pour tout n, Xn et X ont un moment d'ordre p fini et si
où de manière équivalente, si
Dans ce cas on note .
Remarques :
- Le fait que et aient un moment d'ordre p fini implique que aussi (pour p ≥ 1 cela est une conséquence de l'inégalité de Minkowski). Ainsi la quantité est bien définie. Plus précisément l'ensemble des variables aléatoires réelles définies sur ayant un moment d'ordre p fini est un espace vectoriel réel pour lequel la fonction est une semi-norme, quand p ≥ 1, et est une semi-quasi-norme, quand 0 < p < 1. Attention ce n'est pas une norme, en général on quotiente par le sous-espace des variables aléatoires presque-sûrement nulles. Sur cet espace quotient, induit une norme quand p ≥ 1 et induit une quasi-norme quand 0 < p < 1.
- Pour p = 1, on parle simplement de convergence en moyenne et pour p = 2 de convergence en moyenne quadratique.
- La convergence en moyenne d'ordre p se généralise à des variables aléatoires à valeurs dans un espace vectoriel normé muni de sa tribu borélienne. Il est même possible de généraliser cette notion de convergence à des fonctions mesurables sur un espace mesuré.
- Pour r =2, on a le résultat suivant :
Propriété — Soit c une constante réelle. On a alors
si et seulement si
Convergence presque sûre
On rappelle qu'un ensemble négligeable de l'espace probabilisé est un sous-ensemble tel qu'il existe vérifiant et . Autrement dit, un ensemble négligeable est un sous-ensemble de inclus dans un ensemble de probabilité nulle.
Définition (convergence presque sûre) — On dit que (Xn) converge presque sûrement vers X si
ou de manière équivalente, s'il existe un ensemble négligeable N ⊂ Ω tel que
Dans ce cas on note .
Remarques :
- L'ensemble appartient bien à la tribu , donc sa probabilité est bien définie. En effet cela peut se voir en écrivant et en utilisant les propriétés de stabilité d'une tribu.
- La convergence presque sûre est équivalente à la condition :
- ainsi qu'à la condition :
- où ces limites inférieure et supérieure de suites d'ensembles sont définies par
- et
.
- La convergence presque sûre est utilisée dans la loi forte des grands nombres.
- La convergence presque sûre se généralise à des variables aléatoires à valeurs dans un espace topologique muni de sa tribu borélienne. Il est même possible de généraliser cette notion de convergence à des fonctions mesurables sur un espace mesuré, on parle alors de convergence presque partout.
Convergence en probabilité
Définition (convergence en probabilité) — On dit que (Xn) converge vers X en probabilité si
Dans ce cas on note .
Remarques :
- La convergence en probabilité se généralise à des variables aléatoires à valeurs dans un espace métrique muni de sa tribu borélienne. Dans ce cas il faut remplacer par dans la définition, où désigne la distance. Il est même possible de généraliser cette notion de convergence à des fonctions mesurables sur un espace mesuré, on parle alors de convergence en mesure.
Convergence en loi
Définition (convergence en loi) — On dit que (Xn) converge vers X en loi si pour toute fonction f à valeurs réelles, continue et bornée
Dans ce cas on note ou encore .
Remarques :
- Le fait que soit continue nous assure qu'elle est mesurable, donc par composition, et aussi. De plus, le fait que soit bornée implique que et sont aussi bornées. Ainsi les quantités et sont bien définies.
- Dans le cas de variables aléatoires à valeurs entières, la convergence en loi est équivalente à :
- pour tout entier m.
- Dans le cas de variables aléatoires à valeurs réelles, il existe un critère de convergence en loi important faisant appel aux fonctions de répartition. Plus précisément, soient F1, F2, ... la suite des fonctions de répartition associées aux variables aléatoires réelles X1, X2, ... et F la fonction de répartition de la variable aléatoire réelle X. Autrement dit, Fn est définie par Fn(x) = P(Xn ≤ x), et F par F(x) = P(X ≤ x). La suite (Xn) converge vers X en loi si et seulement si
- pour tout réel a où F est continue.
- Puisque F(a) = P(X ≤ a), cela signifie que la probabilité que X appartienne à un certain intervalle est très proche de la probabilité que Xn soit dans cet intervalle pour n suffisamment grand.
- Un autre résultat important donnant des critères équivalents de convergence en loi est le théorème porte-manteau.
- Le théorème de convergence de Lévy donne une équivalence entre la convergence en loi et la convergence, en tout point, des fonctions caractéristiques.
- La convergence en loi se généralise à des variables aléatoires à valeurs dans un espace topologique muni de sa tribu borélienne.
Exemples
Convergence en loi
La moyenne d'une suite de variables aléatoires centrées et de carré intégrable, indépendantes et de même loi, une fois renormalisée par √n converge en loi vers la loi normale
La loi de Student de paramètre k converge, lorsque k tend vers +∞, vers la loi de Gauss :
Dans ce cas, on peut aussi utiliser le lemme de Scheffé, qui est un critère de convergence d'une suite de variables aléatoires à densité vers une variable aléatoire à densité.
La suite[1] converge en loi vers une variable aléatoire X0 dite dégénérée, qui prend une seule valeur (0) avec probabilité 1 (on parle parfois de masse de Dirac en 0, notée δ0) :
Convergence d'une fonction d'une variable aléatoire
Un théorème très pratique, désigné en anglais généralement sous le nom de mapping theorem (en), établit qu'une fonction g continue appliquée à une variable qui converge vers X convergera vers g(X) pour tous les modes de convergence :
Théorème — (Mapping theorem[2]) Soit une fonction continue en tout point d'un ensemble C tel que :
- Si ;
- Si ;
- Si .
En statistiques, un estimateur convergent de la variance σ2 est donné par :
- .
On sait alors par le continuous mapping theorem que l'estimateur de l'écart type σ = √σ2 est convergent, car la fonction racine est une fonction continue.
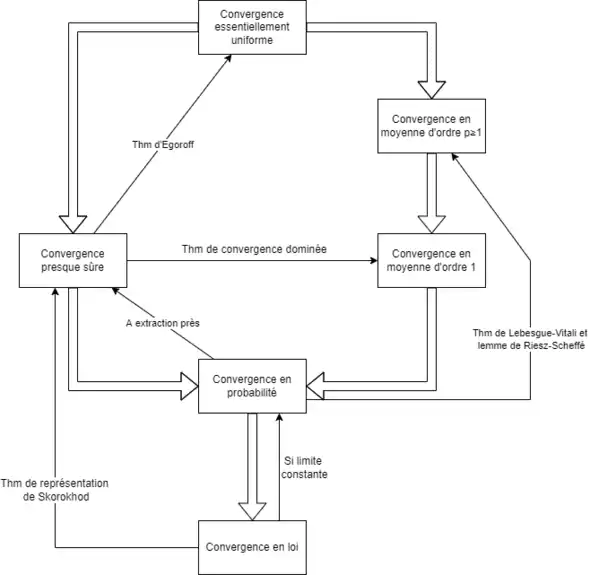
Liens entre les différents modes de convergence
Convergences L∞ et Lp
Propriété (L∞ implique Lp) — Soit . Si et sont essentiellement bornées et si alors .
À noter que si et sont essentiellement bornées, alors elles admettent un moment d'ordre p fini. Il est donc légitime de parler de la convergence en norme .
La réciproque du résultat est fausse. Par exemple, prenons une suite de variables aléatoires à valeurs dans telles que pour tout . Alors, pour tout , converge vers 0 en norme car . Pourtant elle ne converge pas en norme car .
Convergences Lp et Lq
Propriété (Lp implique Lq pour p > q ≥ 1) — Soit . Si et sont dans et si alors .
À noter que si et ont un moment d'ordre p fini, alors elles ont aussi un moment d'ordre q fini. Il est donc légitime de parler de la convergence en norme .
La réciproque du résultat est fausse. Par exemple, prenons une suite de variables aléatoires à valeurs dans telles que et pour tout . Alors converge vers 0 en norme car . Pourtant elle ne converge pas en norme car .
Convergences Lp et en probabilité
Propriété (Lp implique en probabilité) — Soit . Si et sont dans et si alors .
La réciproque du résultat est fausse. Par exemple, prenons une variable aléatoire de loi uniforme sur et posons . Alors converge vers 0 en probabilité car pour . Cette suite converge même presque sûrement vers 0. Pourtant elle ne converge pas en norme car . Le théorème de Lebesgue-Vitali et le lemme de Riesz-Scheffé[3] donnent chacun une condition suffisante pour que la convergence en probabilité donne la convergence en moyenne d'ordre p. La condition du premier est l'uniforme intégrabilité et la condition du second est la convergence des moments d'ordre p.
Théorème (Lebesgue-Vitali) — Soit . Supposons que les trois propriétés suivantes sont vérifiées.
- La suite est dans .
- La suite converge vers en probabilité.
- La suite est uniformément intégrable.
Dans ces conditions on a que est dans et .
Lemme (Riesz-Scheffé) — Soit . Supposons que les quatre propriétés suivantes sont vérifiées.
- La variable est dans .
- La suite est dans .
- La suite converge vers en probabilité.
- On a que .
Dans ces conditions on a que .
Convergences L∞ et presque sûre
Propriété (L∞ implique presque sûre) — Si et sont essentiellement bornées et si alors .
La réciproque du résultat est fausse. Par exemple, prenons une variable aléatoire de loi uniforme sur et posons . Alors la suite converge vers 0 presque sûrement mais elle ne converge pas vers 0 dans car pour tout . Le théorème d'Egoroff donne une réciproque partielle : s'il y a convergence presque sûre, alors il y a convergence uniforme sur des évènements de probabilité aussi proche de 1 que l'on souhaite (sans jamais atteindre 1 exactement).
Théorème (Egoroff) — Supposons que converge vers presque sûrement. Alors pour tout il existe un évènement tel que et tel que converge uniformément vers sur . Autrement dit,
À noter que dans le théorème d'Egoroff la convergence est uniforme ce qui est plus fort que la convergence essentiellement uniforme.
Convergence presque sûre et en probabilité
Propriété (presque sûre implique en probabilité) — Si converge vers presque sûrement alors converge vers en probabilité.
La réciproque du résultat est fausse. Par exemple prenons une variable aléatoire de loi uniforme sur . On crée les intervalles , , , , , , , , ... Plus explicitement, pour tout on pose et . On crée alors . On définit ensuite . Alors la suite converge en probabilité vers 0. Elle converge même dans pour tout car . Pourtant cette suite ne converge pas presque sûrement vers 0 car presque sûrement il existe une infinité de tels que . Il est également possible de trouver des suites qui convergent en probabilité mais qui converge ni presque sûrement, ni dans comme le montre l'exemple suivant.
Soit p > 0. On considère (Xn)n ≥ 1 une suite de variables aléatoires indépendantes telle que
La suite (Xn)n converge en probabilité vers 0 car
En revanche, elle ne converge pas dans car
Montrons qu'elle ne converge pas non plus presque sûrement. Si c'était le cas sa limite presque sûre serait nécessairement sa limite en probabilité, à savoir 0. Or, comme et comme les variables aléatoires Xn sont indépendantes, on a par la loi du zéro-un de Borel :
i.e. presque sûrement Xn = n1/p pour une infinité de n. Donc, presque sûrement, A fortiori Xn ne converge pas presque sûrement vers 0.
Dans l'exemple précédent, pour éviter le recours à la loi du zéro-un de Borel, on peut définir explicitement la suite Xn de la façon suivante. On choisit Ω = [0,1] muni de sa tribu borélienne et de la mesure de Lebesgue. On pose , pour , puis
Enfin on définit
Les Xn ainsi définis ne sont pas indépendants mais ils vérifient comme dans l'exemple précédent
Les trois propriétés suivantes donnent des réciproques partielles. La première dit que la convergence en probabilité implique la converge presque sûre d'une sous-suite. La deuxième est une conséquence du théorème de Borell-Cantelli et dit que si la convergence en probabilité a lieu assez rapidement alors la convergence presque sûre a lieu également. Enfin, la troisième dit que la convergence en probabilité est équivalente à la convergence presque sûre pour une somme de variables aléatoires indépendantes[4],[5].
Propriété — Si converge vers en probabilité, alors il existe une extraction telle que converge vers presque sûrement.
Propriété — Si pour tout
alors converge vers presque sûrement.
Propriété — Si les sont indépendantes et si on note pour tout , alors la suite converge presque sûrement si et seulement si elle converge en probabilités.
Convergence en probabilité et en loi
Lemme — Si l'on a les convergences suivantes, respectivement dans (E,d) et dans
alors on a
dans l'espace E × E muni de la distance infinie.
Propriété — Si Xn converge vers X en probabilité alors Xn converge vers X en loi.
Théorème de Slutsky — Si Xn converge en loi vers X, et si Yn converge en probabilité vers une constante c, alors le couple (Xn ,Yn) converge en loi vers le couple (X,c).
Convergence presque sûre et en loi
La convergence presque sûre implique la convergence en loi, puisqu'elle implique la convergence en probabilité et cette dernière implique celle en loi. La réciproque est fausse. Le théorème de représentation de Skorokhod donne une réciproque partielle.
Notes et références
- Pour plus de détail sur cet exemple, voir Davidson et McKinnon 1993, chap. 4.
- Vaart 1998, p. 7.
- (en) N Kusolitsch, « Why the theorem of Scheffé should be rather called a theorem of Riesz », Periodica Mathematica Hungarica, vol. 61, , p. 225-229 (lire en ligne)
- (en) « how to show convergence in probability imply convergence a.s. in this case? », sur StackExchange,
- (en) Kai Lai Chung, A Course in Probability Theory, Academic Press, 3e éd. (lire en ligne), p. 126 (Théorème 5.3.4)
Bibliographie
- Russell Davidson et James McKinnon, Estimation and Inference in Econometrics, New York, Oxford University Press, , 874 p. (ISBN 978-0-19-506011-9, LCCN 92012048), p. 874
- (en) G. R. Grimmett et D. R. Stirzaker, Probability and Random Processes, Oxford, Clarendon Press, , 2e éd. (ISBN 0-19-853665-8), p. 271-285
- (en) Adrianus Willem van der Vaart (trad. de l'allemand), Asymptotic Statistics, Cambridge, Cambridge University Press, , 1re éd., 443 p., relié (ISBN 978-0-521-49603-2, LCCN 98015176), p. 443