Timée (Platon)
Le Timée (en grec ancien : Τίμαιος / Tímaios), l'un des derniers dialogues de Platon, est considéré depuis l'Antiquité comme l'œuvre capitale du philosophe. Rédigé sans doute vers , à peu d’intervalle du Politique et du Philèbe, mais avant Les Lois, comme le montrent les nombreuses analogies entre ces trois dialogues, le Timée devait composer une trilogie avec le Critias et l’Hermocrate, mais rien de ce dernier dialogue ne nous est jamais parvenu. Cette trilogie avait pour projet de décrire les origines de l'univers, de l'homme et de la société.
Pour les articles homonymes, voir Timée.

| Titre original |
(grc) Τίμαιος |
|---|---|
| Format | |
| Langue | |
| Auteur | |
| Genre | |
| Personnage | |
| Date de parution |
| Série |
|---|
L'ouvrage présente une vaste cosmogonie fondée sur les données les plus certaines de la science, telle qu'elle se développait au milieu du IVe siècle av. J.-C., dans un climat de curiosité intellectuelle et de partage incessant du savoir. C'est un philosophe pythagoricien, probablement fictif, du nom de Timée de Locres, qui expose une réflexion sur l'origine de l’univers, la nature du monde physique et la formation de l'Âme du monde vues comme les œuvres d'un démiurge, tout en abordant les questions de la connaissance scientifique et de la place des mathématiques dans l'explication du monde. Platon y développe une cosmologie dans laquelle prennent place les théories novatrices du lieu, du Temps et des transformations mutuelles des éléments, expression de la puissante stimulation intellectuelle que les nouvelles découvertes astronomiques et mathématiques ont donnée au monde philosophique de son époque.
Cette cosmologie constitue une encyclopédie complète de la science platonicienne, indispensable au philosophe et à l’homme d’État. Platon y rattache une anthropologie, partie maîtresse du dialogue relative à l’homme, dans laquelle il dessine non seulement l’histoire fictive de l’humanité et de la cité d’Athènes, mais où il esquisse aussi une psychologie morale fondée sur l’imitation par l’homme de la divine harmonie cosmique. Le pressentiment qu’il existe du divin dans le cosmos, qualifié de « dieu visible » par Platon et par Aristote, inaugure ainsi un changement décisif dans l’histoire de la religion grecque, et annonce la théologie de l’époque hellénistique et de l’Antiquité tardive. Le profond sentiment religieux qui anime le Timée, conséquence de l’idéalisme spéculatif de Platon, fonde l’optimisme de sa philosophie : puisque nous pouvons, autant qu’il est en nous, nous identifier à l’œuvre de Dieu grâce à la raison, notre salut nous appartient, il réside dans la pensée. Cette conviction anime aussi bien ses plans de réformation morale et politique que ses conceptions médicales.
L'étendue et l’importance des questions traitées dans ce dialogue qui contient une philosophie de l'histoire rattachée à une conception générale de la nature, explique la lecture ininterrompue qui en a été faite à travers les siècles par les philosophes et les savants, et la profonde influence qu’il a pu exercer dans quasiment tous les domaines du savoir, depuis l'Antiquité jusqu’aux débuts du christianisme et à la Renaissance. Malgré les grandes différences qui séparent notre savoir scientifique de celui en vigueur à l’époque de Platon, ce que l’historien de la philosophie, Walther Kranz, appelle « l’atomisme mathématique » du Timée, a été retenu par certains savants du XXe siècle comme une hypothèse anticipant les plus récentes découvertes de la physique.
Présentation générale
Une encyclopédie

Le Timée présente une composition méthodique et pédagogique, avec des articulations nettement marquées : annonces des développements qui vont suivre, récapitulations des résultats acquis et pas moins de dix résumés. C’est aussi le dialogue dans lequel l’exposé continu d’un seul personnage, Timée de Locres, occupe la quasi-totalité de l’œuvre. Autant de procédés qui donnent à ce dialogue l’allure d’un cours destiné non à des profanes mais à un auditoire déjà « familier avec les méthodes de la science » (53 c), comme Platon le fait remarquer lui-même[1]. Sous son apparence de fiction, le caractère scientifique et positif du Timée ne doit pas être méconnu : Platon expose avec précision, et dans une langue technique, l’état le plus récent des connaissances de son temps, mais sans prétendre être exhaustif[2]. En effet, loin de se limiter à la cosmologie et aux interrogations sur la nature du monde physique, le Timée aborde les mathématiques, la biologie, la chimie, la médecine, la psychologie, la politique, la religion et l’astronomie.
Une histoire fictive et une Genèse
Dans cette encyclopédie, tout ce qui touche à la description de l’univers, à la physique et à la formation de l’Âme du Monde n’est pas l’essentiel aux yeux de Platon : la cosmologie joue un rôle accessoire par rapport à l’anthropologie. On le voit à la requête amicale que Socrate adresse à ses trois interlocuteurs. Il leur demande de faire l’éloge de la cité idéale qu’il a décrite la veille[note 1], en racontant comment, de théorique et abstraite, on peut imaginer son excellence en action[3]. Pourrait-on en construire le modèle vivant et montrer sa perfection face aux difficultés de la réalité, en temps de paix et de guerre (18 b-20 c) ? Tel est l’objet principal du Timée : l’intention du dialogue est politique. Critias fait alors le récit de la guerre victorieuse menée par Athènes, il y a neuf mille ans, contre l’ennemi atlante et la chute de l’Atlantide. C’est ainsi que, par un artifice, Platon prétend nous raconter l’histoire oubliée — mais en réalité, fictive — de l’humanité et de la cité d’Athènes : livre des générations, le Timée comme le Livre de la Genèse, ramène un peuple au souvenir de ses origines et de ses ancêtres pour mieux l’enraciner dans l’ordre universel[4]. Il cherche aussi à fonder la constitution idéale décrite dans La République en montrant que dans la plus haute antiquité, avant le déluge, à Athènes, les choses étaient conformes à ce modèle d’excellence, qui lui-même répondait aux fins d’un être humain qui trouvait sa place dans cette cité et cet univers organisé. De la sorte, Platon dote son récit de l’autorité de l’histoire ; et en rattachant cette histoire à l’histoire de l’univers, il la fait bénéficier aussi de l’autorité de la science physique, tout en mettant en relief l’unité des choses[5].
Microcosme et macrocosme
Dans le Timée, la physique de Platon, au sens grec d’« étude de la nature », est téléologique : c’est dire que « la destinée de l’homme y est considérée comme la fin de la Nature », écrit Léon Robin[6]. Ce qui demeure toujours au centre de la réflexion de Platon, c'est donc l’homme. Toutes les sciences, même les plus abstraites, ne sont étudiées que dans leurs rapports à la science de l’homme. Ainsi, l’origine des végétaux ou l’histoire des animaux ne sont traitées accessoirement qu’à l’occasion de la nutrition ; de même, la physique, la minéralogie, la chimie ne sont abordées que sous l’angle qui intéresse directement l’humanité, au point de vue des sensations, de l’hygiène, de la thérapeutique, ou de propriétés dont nous pouvons faire notre profit[7]. Cette histoire naturelle de l’homme, qui commence avec Phoroneus, « celui qu’on appelle le premier homme » (22 a), est conduite en vue de ses applications pratiques à l’éducation, à la médecine et à la politique. Elle entre dans la conception globale d’une liaison étroite entre nature humaine et nature universelle, entre microcosme et macrocosme. Cette conception du Timée dominera toute la philosophie de la Renaissance et du XVIIe siècle.
Composition du Timée
Aussitôt après le prologue (17 a-27 b), le personnage de Critias annonce le choix du plan qui sera suivi en fonction de l’étude projetée de l’univers puis du microcosme humain : « Il nous a paru que Timée, celui d’entre nous qui est le meilleur astronome et qui a donné le plus de travail à pénétrer la nature de l’Univers, devait prendre la parole le premier et, partant de la naissance du monde (τῆς τοῦ κόσμου γενέσεως), terminer par la nature de l’homme (ἀνθρώπων φύσιν) (27 a). » Ce programme soulève le problème philosophique fondamental de la connaissance : peut-on embrasser dans un même discours rigoureux une cosmologie et une anthropologie ? L’homme peut-il accéder à la vérité au sujet de l’univers, de la politique et du divin ? Platon pose alors quatre principes généraux, distinguant l’Être qui est toujours et ne devient pas ; le raisonnement et l’opinion fondée sur la sensation irraisonnée ; la causalité nécessaire au commencement de tout devenir ; enfin le modèle éternel, intelligible et immuable[8]. Il énonce ensuite les conséquences méthodologiques et épistémologiques qui résultent de ces principes pour sa recherche.
- Dans une première partie (de 27 d à 47 e), il expose la loi suivant laquelle la pensée de Dieu ou sa sagesse inspirée par sa bonté, a dû, vraisemblablement, organiser un monde le meilleur possible[9] : c’est l’action de la « cause intelligente (ou divine) », celle qui est à l’origine de l’Univers et de la destinée des âmes.
- Dans une deuxième partie (de 48 a à 68 e), Platon expose l’action de la « cause nécessaire » (δι’ἀνάγκης), dont la nature est de mouvoir, de façon indéterminée[10] ; dans l’étude de la physique, sont abordés les corps élémentaires et leurs transformations mutuelles, la minéralogie, la chimie (hydrométéores, propriétés des métaux…) et la théorie des sensations[11].
- Enfin, dans une troisième partie (de 69 a jusqu’à la fin du dialogue), Platon montre comment se sont associées les deux causes (« cause nécessaire » aussi appelée « cause errante ») sous l’autorité de la « cause intelligente »[12]. Ainsi commence l’histoire naturelle de l’homme en qui le principe immortel de l’âme s’allie à un corps mortel ; elle se développe avec un traité d’anatomie, de physiologie, de pathologie, d’hygiène et de thérapeutique[13].
Personnages et exécution rhapsodique

Les quatre personnages du Timée, Socrate, Critias, Hermocrate et Timée de Locres, sont réunis pour un festin (δαιτυμών, ἑστίασις, 17 a, 27 b), lié à la fête des Panathénées et aux concours rhapsodiques qui s’y déroulaient ; Platon file donc, tout au long du prologue, la métaphore d’une exécution rhapsodique, chaque personnage prenant le relais du discours du précédent, selon l’antique tradition établie par Solon[14].
Socrate a pris la parole le premier pour résumer les principales caractéristiques de la Cité idéale, et par la suite il est réduit au rôle d’interlocuteur muet. Le philosophe et homme politique Critias, par son récit historique, a confirmé la peinture faite par Socrate.
Le personnage d’Hermocrate ne joue quasiment aucun rôle dans le dialogue et fait surtout figure d’auditeur ; il a été identifié par Proclus avec un personnage historique, le fameux général syracusain du même nom, ennemi acharné des ambitions d’Athènes[15] : Platon aurait ainsi ironiquement confié au glorieux stratège, vainqueur des Athéniens, le soin de déterminer leur futur régime politique. Le troisième dialogue de la trilogie projetée par Platon, qui devait porter le nom d’Hermocrate et où il aurait tenu le rôle principal, n’a sans doute jamais été écrit[16], et nous ignorons le thème que Platon aurait traité dans ce dialogue.
Timée, le personnage principal du dialogue, est présenté comme « un citoyen de la ville si bien policée de Locres en Italie », un homme qui se distingue par la fortune et la naissance. Socrate souligne les qualités éminentes de Timée comme homme d’État et l’excellence des institutions politiques de Locres : il aurait « participé aux plus grandes charges et aux plus grands honneurs de sa patrie », tout en s’élevant aux sommets de toute philosophie (20 a). Il est aussi versé dans les mathématiques et l’astronomie plus qu’aucun autre des personnages du dialogue, et le discours qu’il prononce est de tendance nettement pythagoricienne. Mais ce personnage mystérieux ne nous est connu que par le témoignage de Platon[17]. Il a peut-être existé un savant pythagoricien portant le nom de Timée de Locres, mais aucune source ne permet de l'affirmer[18] ; l’hypothèse qui domine chez la plupart des commentateurs est celle d’un personnage de fiction, forgé sur le portrait du mathématicien et savant pythagoricien Archytas de Tarente : sous le nom de Timée, Platon aurait ainsi rendu hommage à son ami qu’il ne pouvait nommer expressément, puisque le discours de son personnage ne représentait pas exactement les conceptions du Tarentin[19].
Une cosmologie mathématique et révolutionnaire
On a pu dire que la cosmologie du Timée prolongeait les projets des physiologues présocratiques qui, dès le VIe siècle av. J.-C., avaient pris le relais des poètes dans la tentative d’offrir une explication de l’origine comme cause et de l’évolution du monde visible, le cosmos (κόσμος), depuis le Chaos primordial : alternative rationnelle à la cosmogonie des récits mythiques à la manière d’Hésiode au VIIIe siècle av. J.-C.[20]. De fait, le Timée est le tout premier ouvrage de cosmologie à nous être parvenu dans son intégralité. Dans divers textes intitulés Sur la nature (en grec ancien Περὶ φύσεως), des penseurs, parmi lesquels Anaximandre, Héraclite, Empédocle, et Parménide, avaient produit un discours qui, au-delà de l’univers physique (macrocosme), traitait aussi du microcosme, de l’origine et de la nature des êtres vivants, de l’homme et de la société, offrant par là une vision politique pour un modèle d’organisation de la cité fondé sur une vision du monde.
Mais la cosmologie du Timée s’écarte de celle des présocratiques sur deux points essentiels. Platon innove puissamment sur le plan philosophique et métaphysique, en concevant le monde et tous les êtres vivants qui le composent comme une création qui n’avait rien de nécessaire, comme un acte de pure générosité. Selon le mot d’André Motte, « il révolutionne la cosmologie traditionnelle dans ses rapports avec la théologie et l’éthique, et fait jaillir un monde vivant et harmonieux par l’acte libre d’une intelligente et transcendante Bonté[21]. » Poussant la spéculation sur le cosmos dans la voie jusque-là inexplorée des découvertes scientifiques les plus récentes, Platon est aussi le premier à penser l’univers en termes géométriques et mathématiques[22] : « Le Timée contient l’acte de naissance de la physique mathématique », écrit Bertrand Saint-Sernin[23]. L’information mathématique, reçue du monde intelligible et soulignée par Platon par l’expression ἀνὰ λόγον, constitue le ciment (ξυνδεσμός) qui assure à l’univers sa stabilité et sa continuité[24]. Kepler aussi bien que Galilée ont reconnu le bien-fondé de cette démarche que l’on peut qualifier de « modélisation mathématique[25] » pour rendre compte de la constitution de l’univers[26]. Galilée, lui aussi, affirme en 1623 : « L’univers est écrit dans la langue mathématique, et ses caractères sont des triangles, des cercles, et autres figures géométriques[27]. »
Le pari des Formes intelligibles
Si Platon postule une physique mathématique de l’univers, c’est à la fois en vertu d’une conviction ancienne et d’un pari. Le Timée repose en effet sur l’hypothèse des Idées ou des Formes intelligibles, c’est-à-dire sur une réalité d’un ordre suprasensible définie dans le Phédon comme « ce qui est divin, immortel, intelligible (νοητόν), ce dont la forme est une (μονοειδές), ce qui est indissoluble (ἀδιάλυτον) et possède toujours en même façon son identité à soi-même (ἀεὶ ὡσαύτως κατὰ ταὐτὰ ἒχον)[A 1]. » Ces termes sont très exactement ceux employés dans le Timée pour caractériser le modèle idéal dont s’est servi le Démiurge pour organiser le monde visible[A 2]. Platon précise que ce modèle éternel et immuable, « ce sont les Idées que nous ne pouvons percevoir par les sens mais seulement par l’intellect » (51 d). Dès lors l’alternative est posée en ces termes : « Ou bien il y a, imbriquées dans le monde sensible, des entités intemporelles (nombres, figures et solides géométriques, schémas de causalité, etc.) ; ou bien il n’y a que ce qui se voit, se sent, se touche[23]. » Il n’y a pas d’évidence irréfutable d’un côté ou de l’autre, il faut prendre parti. Platon parie : « je vote », dit-il, (τίθεμαι ψῆφον), en faveur de la première option, et il précise aussitôt que « l’intellection naît en nous par l’action de l’enseignement scientifique (διὰ διδαχῆς) et s’accompagne toujours d’une démonstration vraie (μετ’ἀληθοῦς λόγου, 51 e). » La cosmologie et l’anthropologie devront donc être unifiées à l’aide d’une modélisation mathématique, et d’abord pour des raisons ontologiques : Platon conçoit en effet la nature des corps vivants en quelque sorte comme « poussière d’étoiles », les hommes sont faits, dit-il, « d’éléments empruntés à l’univers qui doivent lui être rendus un jour », après la mort (42 e - 43 a).
Recherches et intuitions scientifiques dans le Timée
En matière scientifique, Platon a pris une part considérable au développement de la physique et des mathématiques de son époque, au point d’apparaître non seulement comme un chercheur mais comme l’instigateur de l’essor mathématique du IVe siècle av. J.-C.[28] Les mathématiques sont en effet pour lui l’instrument permettant d’exprimer certaines des conséquences découlant des axiomes posés.
La Lettre VI indique que Platon était en contact avec les scientifiques et les intellectuels pythagoriciens de Grande-Grèce, parmi lesquels figure son ami, le philosophe et mathématicien Archytas de Tarente[29], le modèle présumé de Timée de Locres. Parmi tous les domaines qu’il a abordés, Archytas se distingue par l’étude des proportions numériques appliquées aux intervalles musicaux ; ces recherches sur les rapports numériques le conduisirent à une théorie descriptive du cosmos[30]. Pythagore et Archytas établissent en effet un lien étroit entre harmonie musicale et harmonie universelle[A 3], or Platon fait de même dans le Timée (47 d) : Archytas a donc pu fonder la doctrine harmonique du Timée[31].

Le Timée conserve aussi le souvenir des travaux de recherche effectués dans tous les domaines scientifiques au sein de l’Académie, et montre combien Platon souhaitait être à la pointe de l’actualité scientifique de son époque. Ainsi, le dialogue suppose connus le théorème de Pythagore et la théorie des quantités irrationnelles formulée par Théodore de Cyrène, le maître de Platon ; les mathématiques d’Eudoxe de Cnide et la méthode d'exhaustion apparaissent à la source du système cosmologique de Platon, en particulier dans les divisions du mélange utilisé par le démiurge pour combler les intervalles dans les séries créées pour l’Âme du monde (35 b-36 b)[33] ; le Timée utilise la théorie des médiétés et la théorie des polyèdres réguliers (54 e - 56 c) qui se sont développées précisément à l’époque de Platon, dans le milieu socratique[34] ; c'est Théétète, l’ami de Socrate et de Platon, qui, le premier démontre qu’il ne peut y avoir que cinq polyèdres réguliers convexes inscriptibles dans la sphère : la pyramide à 4 sommets, le cube, l’octaèdre, le dodécaèdre et l’icosaèdre, utilisés dans le dialogue[22] ; c’était à cette époque une nouveauté mathématique, comme Platon le dit lui-même (48 b). Concernant l’atomisme platonicien, bien qu’il ne se réfère jamais explicitement ni à Leucippe ni à Démocrite, le Timée présente d’assez nombreuses ressemblances avec la physique de Démocrite, dont la doctrine était répandue à l’époque de Socrate. Ce dialogue suppose une théorie corpusculaire — les figures solides élémentaires constitutives des quatre éléments sont à peu près semblables aux atomes de Démocrite — mais sans l’espace vide des atomistes, et dans une interprétation finaliste de la nature, sous la loi du Bien[35]. Ces particules élémentaires sont animées d’un mouvement naturel uniforme, semblable à celui de l’Âme du monde et des planètes dans le système cosmologique de Platon : considérée à la lumière de la mécanique classique, cette conception de la nature du mouvement n’est pas autre chose que la première intuition du principe d’inertie[36]. Enfin, en biologie et médecine, le Timée présente, sur les organes des sens, une doctrine semblable à celle d’Empédocle, d’Alcméon et du Corpus hippocratique[37]. Au cours de ses voyages en Sicile, entre et , Platon s’est lié d’amitié avec le célèbre anatomiste Philistion de Locres, chirurgien et chef de l’école de médecine dont il reprend globalement les idées en matière d’anatomie, et il ne s’en écarte que sur le siège de l’intelligence et la question des sensations[38].
Un mythe vraisemblable et rationnel
La genèse du cosmos est un évènement originel inaccessible à l’homme[39], Platon raconte donc les évènements tels qu’ils auraient pu ou auraient dû arriver. Le récit cosmologique du Timée ne peut être qu’une fable vraisemblable (εἰκότα μῦθον, 29 d). En tant que mythe, le récit prend ainsi la forme d’une narration qui se déploie dans le temps, et qui décrit ce que font des personnages (40 a). La nécessité de recourir au mythe s’explique par la distinction entre deux formes de connaissance, d’une part la science, qui fonde un savoir irréfutable au moyen de démonstrations rigoureuses et que la persuasion ne peut ébranler (51 d), et d’autre part les opinions vraisemblables (29 b) ; l’opinion est une fluctuation de pensée qu’entraîne le discours vrai ; le discours vrai ne peut porter que sur ce qui est et non sur ce qui devient (29 c-d ; 35 a-d ; 48 b) :
« L’intellection (νοῦς) et l’opinion vraie (δόξα ἀληθής) sont deux choses distinctes, car elles ont des origines distinctes, et se comportent de façons différentes : la première, l’intellection, vient de la science ; on nous persuade la seconde, l’opinion. La première s’accompagne toujours d’une démonstration vraie, l’autre est sans démonstration (ἄλογον) ; l’une est inébranlable par la persuasion, l’autre peut être modifiée par elle. À l’opinion, tout homme participe ; à l’intellection au contraire, les dieux ont part, mais des hommes, une petite catégorie seulement. (Timée, 51 e) »
Platon fait également la distinction entre cause nécessaire et raison vraisemblable (εἰκότα λόγον), et il n’hésite pas à répéter maintes fois le caractère conjectural de son discours[40], allant même jusqu’à considérer parfois que la connaissance qu’il cherche, « nul homme n’en est actuellement capable, ni sans doute ne le sera jamais à l’avenir. » (68 d). Le monde sensible que va décrire Platon n’est qu’une copie d’une forme intelligible, le « Vivant en-soi ». Le discours que tient Timée ne peut donc être dit vrai, il ne peut qu’être semblable au discours vrai. Seul le discours sur les formes intelligibles peut être considéré comme un discours vrai[41]. Le philosophe ne peut guère plus, et fera donc comme le poète : tenir un discours qui ne pourra être dit vrai ou faux, car nul n’aura pu en être le témoin. Enfin, la certitude affirmée par Platon que l’être humain est la proie d’erreurs et d’illusions des sens, et sa « critique de la raison, dont l’inflexibilité vaut celle de Kant ou même la dépasse[42] », a pu contribuer à donner l’impression que le Timée n’était qu’une fable distrayante mais sans valeur.
En réalité, la vraisemblance, notée par l’épithète εἰκώς, utilisée à dix-neuf reprises dans le Timée pour qualifier le mythe[43], loin de l’affaiblir, fonde au contraire l’autorité du récit : « Platon insiste moins sur le caractère fictif de sa narration, qui est évident, que sur les raisons qu’il a de la croire vraisemblable, et sur l’exceptionnelle probabilité de ses inductions[44]. » Il a en effet recours au mythe pour éclairer, de façon approximative, les questions impénétrables par la seule force de la raison discursive[45] ; telles sont les questions métapsychologiques pour lesquelles Platon forge la théorie mythique de la structure psychique de l’homme (72 d). Il fait de même dans le domaine métaphysique et cosmologique, pour expliquer « les dieux et la naissance de l’Univers » (θεῶν καὶ τῆς τοῦ παντὸς γενέσεως)[note 2]. Car non seulement cet univers a été créé à un moment que nous ne connaissons pas, mais en οutre le changement auquel il est soumis dans le flux incessant du devenir crée un principe d’indétermination et d’incertitude ; or, pour Platon, seules les formes intelligibles répondent aux critères de stabilité et de permanence requis par la science[46] ; faute de vérité absolue, c’est donc la vraisemblance du mythe qui permet de formuler, avec le charme de la poésie, une théorie simplement probable[47] : elle fournit un schéma possible pour penser la genèse de l’Univers, comme Descartes le fera aussi dans son Traité du Monde[48]. Cette contemplation philosophique de l’Univers (θεωρία) en imagination est destinée à engendrer en nous la grandeur d’âme en nous faisant vivre dans une perspective cosmique[49]. Même si le Timée reste traditionnel dans sa forme et dans son objet, il est novateur par la nature de l’explication qu’il propose. C’est une théorie du cosmos tout à fait novatrice parce que reposant sur des fondements mathématiques et géométriques, et conforme aux exigences épistémiques énoncées par Parménide en son poème Sur la nature[50] : elle est en effet « rationnelle, dans les limites épistémologiques que Platon s’est fixées, c’est-à-dire fondée sur l'idée du Bien, sur les nombres et les formes géométriques[51]. »
Intellection et opinion
Le récit de Timée est fondé sur des principes épistémologiques et métaphysiques : Platon établit d’abord la distinction entre « ce qui est toujours et ne devient jamais » et « ce qui devient et n’est jamais » (27 d-28 a), le premier étant appréhendé par l’intellection et le raisonnement (νοήσει μετὰ λόγου), le second, par l’opinion jointe à la sensation irraisonnée (δόξῃ μετ’αἰσθήσεως ἀλόγου)[52]. Cette distinction, qui rappelle celle de La République entre l’Intelligible et le sensible[A 4] et qui implique une distinction entre deux formes de la connaissance, soulève la question épistémologique[53]. Selon la conviction platonicienne, il n’y a pas de réalité véritable dans le changement incessant créé par le devenir ; et il n’y a pas de connaissance rigoureuse sans une certaine permanence. Ainsi, le monde sensible, soumis au changement perpétuel, contrairement aux Idées éternelles (εἴδη), qui ne sont ni changeantes ni mouvantes, devrait rester inconnu[54]. Platon résume cette conviction dans cet aphorisme : « Ce que l’Être est au devenir, la vérité l’est à la croyance » (29 c). Or, selon Timée, une explication scientifique doit présenter à la fois un caractère de nécessité et d’idéalité — les deux ne pouvant être déduits de façon immédiate des données de la perception sensible —. Nous ne pouvons donc pas nous fier simplement aux données que nous renvoient nos sens.
Être, Devenir, Khôra
Pour pouvoir connaître le monde sensible, Platon fait donc l’hypothèse de trois types d’entités sans lesquelles le monde sensible resterait inconnu :
- L’être absolu (τὸ ὄν) des formes intelligibles (νοητά), vraiment réelles et immuables : elles peuvent être objets de connaissance rationnelle ;
- L’être relatif des choses sensibles qui naissent (αἰσθητά, γένεσις) ; bien qu’engagées dans le devenir, elles doivent présenter dans leur changement quelque chose qui ne change pas. Pour cela, elles doivent entretenir avec les formes intelligibles un rapport équivalent de copie à modèle. C'est ce qu’Aristote appelle « participation » (τὸ μεταληπτικόν)[A 5] : en tant que copie, celle-ci participe de l’Idée ;
- L’emplacement ou khôra (χώρα) : « lieu » ou espace susceptible de « recevoir » (δεχόμενον) toute création tridimensionnelle[55]. Ce lieu présente une analogie avec le vide, mais sans s’identifier à lui. « La démonstration de l’existence de ce lieu ne peut pas être simplement logique, puisqu’il s’agit d’une essence à laquelle vient s’ajouter un être perçu par les sens ; et elle ne peut pas non plus être tirée d’une donnée directe de la sensation », écrit Albert Rivaud[56].
Dans l’articulation de ces trois concepts, le Timée glisse ainsi de la physique à la métaphysique, même si Platon ne dissocie pas les deux. Le Timée offre donc à la fois une spéculation théorique, physique et métaphysique, et vise en même temps à l’établissement d’une éthique. L’éthique rejoint en effet la physique dans la mesure où la contemplation de l’univers sensible est, selon Platon, une étape indispensable à la contemplation des formes intelligibles — contemplation qui détermine la valeur morale de toute existence humaine. —
Méthode hypothético-déductive
Pour résoudre le problème de la connaissance scientifique, Platon met en place ce qui deviendra la méthode de toute recherche scientifique : la méthode hypothético-déductive. Elle consiste à poser a priori une liste d’axiomes présupposés, puis à vérifier, en se fondant sur des règles d’inférence, de logique, si les propositions que l’on arrive à déduire des axiomes (les théorèmes) présentent une correspondance convenable et raisonnable avec les données des observations. Tel est le point de départ de la thèse soutenue par Luc Brisson et Walter Meyerstein[57] : le Timée serait une théorie scientifique, parce que ce serait une théorie axiomatique de type mathématique, close sur elle-même. Platon y pose cependant les axiomes a posteriori, ses règles d’inférence sont implicites, et il fait peu appel à l’expérience pour montrer la validité de son système : il ne prend pas l’observation comme point de départ, ni comme critère de validité de son système, sauf en de rares exceptions, par exemple relativement à la pesanteur du feu (58 a-59 a)[58], à la formation des odeurs (66 d-67 a)[59], et au rôle des fibres dans le sang (82 c-84 c)[60]. Mais Yvon Gauthier réfute l’ensemble de cette thèse qu’il juge « confuse et fausse »[61] : « La seule présentation d’une théorie sous forme d’axiomes ne suffit pas à en faire une théorie axiomatique au sens où on l’entend aujourd’hui »[62]. On ajoutera que, loin de présenter le Timée comme une théorie scientifique, Platon n’a de cesse, au contraire, de souligner son caractère conjectural mais aussi les limites infranchissables du savoir humain[42] : « Vouloir contrôler tout cela par l’expérience, écrit-il, ce serait méconnaître la différence de la nature humaine et de la nature divine » (68 d).
Le Démiurge, la Nécessité et la Pronoia
La recherche du principe premier, l’arkhè, à l’origine de tout, conduit Platon à une métaphysique de la causalité[63] : cette recherche suppose un effort pour penser la cause originaire hors du temps et hors de toute détérioration due au devenir, cause elle-même nécessairement dépourvue d’origine. Aussi, cette recherche doit-elle s’effectuer, après une prière philosophique (27 c-d), avec la bienveillance des dieux, eux-mêmes principes tutélaires de l’origine[64]. Après avoir présenté les causes auxiliaires ou adjuvantes du mouvement, produisant des effets au hasard et sans ordre, Platon introduit donc la notion d’une causalité supérieure, douée d’intelligence et produisant des choses belles et bonnes (46 d-e) : il s’oppose ainsi radicalement aux physiciens présocratiques[65]. À l’arbitraire d’un mécanisme aveugle, il substitue alors « la présence éternelle d’une cause parfaite, dont les lois de la Nature aussi bien que les mouvements de l’âme sont l’expression dans le temps[66]. » Cette cause parfaite[note 3] est indissociable de la divinité, sous la figure du dieu-artisan et démiurge.
Le Démiurge, « le Dieu intelligible », réunit en lui le savoir-faire d’un parfait artisan, l’activité artistique d’un créateur-poète (ποιητής) et la sollicitude bienveillante d’un père (πατήρ) qui désire que ses enfants lui ressemblent[67]. Il a créé le monde par un mélange de la Nécessité et de l’intelligence ; parce qu’« il était bon, exempt d’envie, le Dieu a voulu que toutes choses fussent bonnes et le plus possible semblables à lui » (29 e - 30 a), écrit Platon, illustrant ainsi la causalité souveraine du Bien : « Sans cette exigence du bien qui l'oblige à réaliser le meilleur par générosité, non seulement le démiurge ne ferait rien, mais il n'y aurait ni démiurge ni modèle, parce qu'il n'existerait ni norme ni valeur[68]. » Aussi le démiurge est-il « la plus parfaite des causes » (29 a), c’est-à-dire la cause qui opère avec le concours de l’intelligence[69].
Dans la naissance du monde, l’action de la Nécessité (ἀνάγκη) se combine avec la pensée. Rompant avec la nécessité de Démocrite et des atomistes pour qui elle est principe de toutes choses, Platon présente cette Nécessité comme une cause instrumentale coopérante au service de la causalité première[70] : l’Intelligence (le Noûs du dieu) domine la Nécessité, qui « cède à la persuasion de la sagesse ; elle réussit à lui persuader d’orienter vers le meilleur la plupart des choses qui naissent » (48 a). Le démiurge façonne ainsi d’abord tout ce qui est immortel dans le monde ; il demande ensuite à ses aides, les dieux jeunes, secondés par l’Âme du monde, de créer les corps périssables ; il travaille tel un artisan dont la fonction principale consiste à mettre en ordre l'Univers[71] ; à cet effet, il doit assurer la présence de l’intelligible dans le sensible sous la forme mathématique[72], et convaincre la Nécessité ; car celle-ci est liée aux propriétés des éléments physiques, elle ne peut pas en être séparée et elle s’impose aux dieux eux-mêmes[73]. C’est une nécessité qu’il y ait dans ce monde de l’imperfection[74]. La Nécessité est aussi liée au hasard ; elle est représentée par ces causes accessoires, « dépourvues d’intelligence » (μονωθεῖσαι φρονήσεως) et génératrices de « n’importe quoi, au hasard et sans ordre »[75] (46 e). Elle semble correspondre à ce que l’on pourrait appeler le pur mécanisme, puisqu’il y a en elle de l’indétermination et du dérèglement (τὸ τυχὸν ἄτακτον)[76] ; Platon relève par exemple comme une exception à la forme la meilleure possible, les parties du corps humain où les besoins contradictoires de résistance et de sensibilité ont imposé un choix préférentiel (75 b)[3].
Platon souligne également « la Providence du Dieu », (en grec ancien : πρόνοια) ; c’est cette providence qui explique l’ordre et les lois que le dieu a préétablis dans le Monde par bonté[77] ; elle se révèle d’abord dans le dessein de créer un Monde qui est lui-même un dieu vivant parfait, doté d’une Âme et d’un corps ; de même, les dieux subalternes, bien que ni immortels ni incorruptibles, demeureront indissolubles, parce que sa volonté expresse constitue un lien plus puissant que les liens de leur naissance (41 a-b)[78] ; quant aux êtres humains, le dieu a veillé à les pourvoir d’une âme apparentée au divin et d’un Intellect (30 c 1, et 44 c 7), facultés de pratiquer la justice et de dominer leurs affections par la raison, afin que lui-même « demeure innocent de la malice future de chacun des êtres », et qu’ils « ne deviennent pas la cause de leurs propres malheurs » (42 a-e)[79]. Le Démiurge apparaît ainsi comme un allié pour l’homme qu’il a aussi doté de la vue, « principe de la plus grande utilité » et dont les bienfaits sont considérables (47 a-b). Dans les textes platoniciens le mot pronoia est rare : il n'est présent qu'en trois dialogues, le Phèdre, le Timée et Les Lois[A 6]. Mais cette rareté relative du terme n'implique pas que la notion de Providence soit, dans la philosophie de Platon, un élément marginal : la Providence est pleinement à l'œuvre dans le livre X des Lois ; et la notion de Providence divine occupe dans la philosophie de Platon une place centrale, dans la mesure où ce n'est qu'en ayant recours à cette notion que Platon peut convenablement résoudre le problème des causes de la génération et de la corruption posé dans les derniers passages du Phédon.
L’Âme du Monde et l’âme du vivant mortel
Les pages du Timée où « Platon décrit de façon saisissante la genèse et l’organisation du cosmos par le démiurge »[80] s’ouvrent sur le premier acte de l’art divin, l’Âme du Monde. Mélangeant d’abord deux essences[81], la substance du Même (ταὐτόν), « indivisible et immuable » (36 d et 37 a) et la substance de l’Autre (θάτερον), divisible et « dont le devenir se manifeste dans les corps »[note 4], le dieu en a composé une troisième, l’essence tout court (οὐσία), mélange des deux précédentes ; mélangeant de nouveau ces trois substances afin d’obtenir leur fusion intime et parfaite, il a obtenu l’essence définitive dont il s’est servi pour sa construction (35 a)[82]. Le démiurge a placé cette essence au centre du corps du monde, il l’a élargie à tout l’univers, de sorte qu’elle l’englobe de toutes parts, et de manière à former « un ciel circulaire, ciel unique, solitaire, capable par sa vertu propre de demeurer en soi-même sans avoir besoin de rien autre, mais se connaissant et s’aimant lui-même parfaitement » (34 b). L’Âme du monde se confond ainsi avec la sphère céleste[note 5] ; sa nature est divine et étant principe de vie, son rôle consiste à assurer les mouvements ordonnés de l’univers[83]. « Recouvrant le ciel de l’extérieur, et tournant en cercle sur elle-même, elle a commencé une vie incessante et sage pour la totalité du temps » (36 e).
Quant à l’âme du vivant mortel, comme son modèle l’Âme du monde, elle est invisible, immortelle, possède les deux cercles du Même et de l’Autre, les mêmes intervalles et a ses révolutions définies par des déterminations mathématiques[84]. Elle ne diffère de l’Âme du monde que par des proportions différentes dans les essences du mélange de fabrication (41 d 6)[85].
Harmonie mathématique et musicale de l'Âme du monde
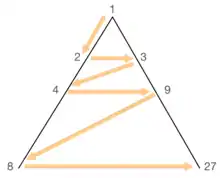
L’Âme du monde est configurée selon des rapports arithmétiques (les nombres qui expriment la division proportionnelle du mélange dont elle est faite), et des rapports géométriques (le rapport des deux cercles de l’équateur céleste et de l’écliptique) (36 b-c). Le mélange définitif imaginé par Platon pour l’Âme du monde est composé de trois substances (que l’on peut appeler par convention A, B, et C) et peut être symbolisé dans la formule mathématique . Le mélange achevé a été divisé en 7 parts qui sont entre elles comme les termes de deux suites géométriques, l’une de raison 2 (1, 2, 4, 8 : suite d’octaves), et l’autre de raison 3 (1, 3, 9, 27 : suite de duodécimes)[86]. Dans ces séries, 4 et 9 correspondent au carré, 8 et 27, au cube. Selon Francis M. Cornford, Platon limite la progression de ces deux suites aux cubes car ceux-ci suffisent à décrire l'espace tridimensionnel tel que nous le percevons[87]. À l’aide de ces deux progressions, le Démiurge a formé une progression unique, et procédé au remplissage des intervalles subsistant entre les termes au moyen de deux médiétés. Dans le langage mathématique grec, on appelle médiété (μεσότης) soit une série de trois termes formant une progression continue, soit le moyen terme qui unit entre eux les deux extrêmes de la progression[88]. Platon connaît la médiété arithmétique, la médiété harmonique et la médiété géométrique[note 6].
D’après deux passages du Timée (36 d et 38 d), l’ensemble de ces valeurs numériques, 1, 2, 3, 4, 9, 8 et 27, représenteraient la valeur du rayon des orbites des planètes[89], mesurée par rapport à la distance de la Lune à la Terre prise comme unité[90] ; ces distances par rapport à la Terre seraient donc : Lune 1 ; Mercure 2 ; Vénus 3 ; Soleil 4 ; Mars 8 ; Jupiter 9 ; Saturne 27.
Pour combler les intervalles qui séparent deux termes consécutifs d’une médiété, Platon associe ces rapports numériques aux intervalles de la gamme diatonique, car il y a parenté entre les proportions de l’échelle musicale et les révolutions de l’âme[91] (47 d) ; il fait appel aux notions, empruntées à la musique, d’épogdoon et de plus petit intervalle ou leimma (en grec ancien : λεῖμμα, « résidu »), qu’il évalue à (36 a-b)[92], soit . L’harmonie de l’Âme du Monde, qui va jusqu’à l’intervalle 27, comprend toutes les gammes possibles et dépasse infiniment les harmonies produites par les instruments de musique[93]. Il faut donc se représenter l’étendue de l’âme, dotée d’un sens inné de l’harmonie, et traversée silencieusement par des mouvements tout à fait analogues aux mouvements du son dans l’échelle musicale[94]. Harmonie musicale et harmonie des mouvements célestes, l’Âme marque le moment décisif dans la génération du cosmos : Platon fait ainsi valoir la puissance du nombre, source de beauté invisible au profane mais familière aux philosophes depuis les travaux des pythagoriciens Philolaos de Crotone et Archytas de Tarente[95].
Fonction intellective de l'âme
Le sens de cette fabrication de l’âme, c’est que dans l’âme, il y a de l’intelligible, du sensible et de l’intermédiaire[81]. L’explication en est donnée par Aristote : « Platon, dit-il, compose l’âme avec les éléments, parce que ce qui connaît doit être semblable à ce qui est connu »[A 7]. Dans le mouvement par lequel elle connaît, l’âme entre en contact tantôt avec l’indivisible (identifié avec le rationnel, τὸ λογιστικόν), et tantôt avec le divisible (identifié avec le sensible, τὸ αἰσθητόν) : dans le premier cas, ce processus produit l’intuition intellectuelle et la science (νοῦς, ἐπιστήμη), dans le second, il produit l’opinion (δόξα) et la sensation (37 b-c). Toujours selon Aristote[A 8], les divers modes de connaissance, dans la doctrine platonicienne, sont symbolisés par les nombres : l’intuition correspond à l’unité, la science à la dualité, l’opinion à la triade, et la sensation à la tétrade. L’âme est donc essentiellement un intellect dans un principe de vie[96]. Il ajoute que l’âme est une grandeur[A 9], non corporelle sans doute mais coextensive au corps[97] : à partir du centre, le démiurge l’a en effet « étendue en tous sens » (ἔτεινεν) jusqu’à la périphérie du corps sphérique du monde, pour l’envelopper tout entier (34 b et 36 e)[98]. Au total, l’âme participe aussi bien à la réflexion raisonnée qu’à l’harmonie des intelligibles éternels (λογισμοῦ μετέχουσα καὶ ἁρμονίας)[99]. Vivifiant et administrant le corps de l’Univers, elle est « ce qui unit le métaphysique au physique »[100].
Cosmogonie
Éléments et solides élémentaires
| Les cinq polyèdres réguliers convexes de Platon | ||||
|---|---|---|---|---|
| Tétraèdre | Hexaèdre ou Cube | Octaèdre | Dodécaèdre | Icosaèdre |
 |
 |
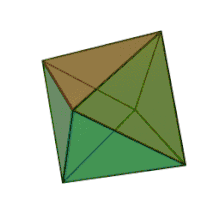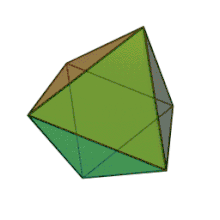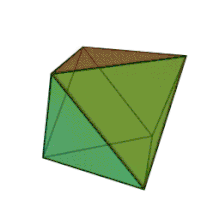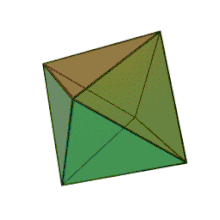 |
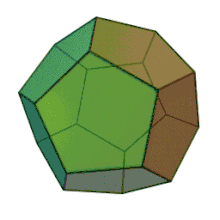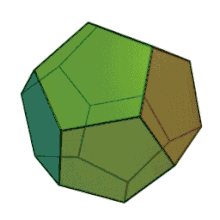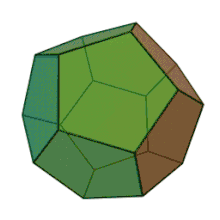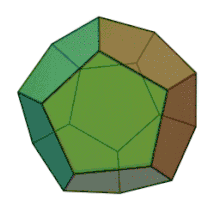 |
 |
Platon s’interroge : est-il possible d’établir une relation rationnelle entre les formes des quatre états de la matière (feu, air, eau, terre) et la diversité des corps composés ?[101] Il répond dans le récit suivant, qui décrit, de façon spectaculaire[102], l’état initial de l’Univers, avant l’intervention du Démiurge.
Au commencement, règnent le désordre et la violence de forces déséquilibrées. La matrice spatiale de la khôra, tout entière embrasée et remplie de « traces » (ἴχνη) de terre, d’eau et d’air, est soumise à des forces erratiques qui la secouent dans tous les sens. Il se produit une chaîne de réactions spasmodiques qui agissent comme un tamis de vannage pour séparer le lourd du léger, et rapprocher les formes semblables des corps élémentaires (52 d-53 b)[102]. À partir de ce début de mise en ordre pré-cosmique, le Démiurge a configuré chacun des quatre éléments « par l’action des Figures et des Nombres », εἲδεσί τε καὶ ἀριθμοῖς (53 b)[103], afin de leur donner leur figure exacte, aussi parfaite que possible. Platon bâtit alors son récit sur des données mathématiques.
Or, « il faut que ce qui naît soit corporel, écrit Platon. De là, vient que Dieu, commençant la construction du corps du monde, a débuté, pour le former, par prendre du feu et de la terre. » (31 b)[note 7]. Le Dieu a donc formé l’univers comme un corps solide (σωματοειδές), visible et tangible, à l’aide de terre () et de feu (), en y adjoignant deux éléments intermédiaires, l’air () et l’eau (), de telle sorte que ces quatre éléments soient dans le même rapport (32 b)[104] ; ils sont unis par le lien le plus fort, celui d’une proportion continue à deux médiétés géométriques telles que l’on ait . En langage moderne, les moyennes recherchées pour les quantités et sont données par les formules : et . Ces formules correspondent à deux problèmes solides : est l’arête d’un cube, équivalent à un prisme droit de hauteur et de base ; est l’arête d’un cube, équivalent à un prisme droit de hauteur et de base . Ces corps solides sont limités par des plans ; or tout plan se résout en triangles[note 8] (triangle isocèle, triangle équilatéral, triangle scalène), à l’aide desquels Platon construit les corps élémentaires : tétraèdre, octaèdre, icosaèdre et cube[105].
En fonction du type de leur base, de leur taille et du caractère plus ou moins saillant de leurs angles solides, chacun des polyèdres présente une affinité avec les propriétés sensibles des éléments[106]. Platon admet en effet, comme Démocrite, cette corrélation entre les propriétés de la matière. Ainsi, le tétraèdre ou la pyramide, avec ses pointes acérées, et sa forme qui est la plus petite et la plus mobile[107], est-il la figure élémentaire du feu, l’octaèdre celle de l’air, l’icosaèdre celle de l’eau, et le cube, forme la plus stable, celle de la terre (55 e - 56 b) : l’attribution de ces formes géométriques aux éléments de la matière reste pour Platon une conjecture vraisemblable[108]. Pour le cinquième polyèdre régulier, le dodécaèdre, « le Dieu s’en est servi pour l’Univers, quand il en a dessiné l’arrangement final[109], » écrit Platon (55 c) : selon Léon Robin, ce serait « une allusion probable aux douze constellations du zodiaque dont le nombre correspond à celui des éléments constituants du dodécaèdre »[110] ; c’est aussi le polyèdre qui s’approche le plus près de la forme d’une sphère, puisque l’Univers doit avoir la forme sphérique voulue par le Démiurge[102]. Et toutes ces figures sont microscopiques au point d’être imperceptibles[111] (56 b-c).
Ces triangles élémentaires ne sont pas conçus comme possédant une taille ultime atomique ; ils sont susceptibles d’acquérir une taille supérieure par assemblage de plusieurs autres triangles ou une taille inférieure par désassemblage, pourvu que soient respectées les deux règles de composition suivantes : 4 triangles rectangles isocèles pour une face du cube, et 6 demi-triangles équilatéraux pour une face des autres polyèdres[112], à l’exception des dodécaèdres.
Le résultat de l’action du Démiurge est une rotation du Monde fini dont « le mouvement se perpétue constamment, pour le présent et pour l’avenir » (58 c)[102].
La météorologie
Dans leurs interactions, les faces des particules des corps simples peuvent se détacher et échanger leurs triangles élémentaires. Le feu, l’eau et l’air se transforment ainsi constamment l’un dans l’autre[113]. Par exemple, deux tétraèdres de feu (deux fois 4 faces) peuvent se transformer en un octaèdre d’air (8 faces). Seuls les cubes de terre ne peuvent pas se transformer avec les trois autres corps élémentaires[114]. Dans le devenir incessant, les éléments doivent être perçus comme choses fuyantes, et non comme des êtres dotés de permanence (49 e, μόνιμα ὄντα)[115]. En tant que choses sensibles, ces corps ne sont que des systèmes instables, une succession d’états changeants[116]. Dans le Timée, Platon esquisse donc l’ébauche d’une météorologie, au sens étymologique du grec μετέωρα / metéôra, c’est-à-dire une étude des corps et des phénomènes célestes dans laquelle existent plusieurs variétés des corps élémentaires (57 c).
Platon explique ainsi que le feu est « de toutes les espèces de corps celle dont les parties sont les plus petites » ; en tant qu'élément, il n’existe pas uniquement sous forme de flamme ; il y a trois sortes de feu : flamme brûlante (φλόξ), lumière, et résidus incandescents de la flamme[117]. Mêlé à l’eau ou à l’air, il produit de la chaleur et joue un rôle dans la digestion ou la respiration (78 a-81 e). Platon distingue deux sortes d’air : la plus pure est l’éther (αἰθήρ) (58 d), région du ciel où reposent les astres et la nuée obscure. L’eau est considérée comme un solide qui ne se liquéfie que sous l’action du feu, comme les métaux ; les hydrométéores que sont la neige, la glace et la grêle sont pour Platon des liquides congelés ; cette conception a perduré jusqu’aux alchimistes du Moyen Âge. La terre enfin contient une proportion plus ou moins grande d’eau ou de feu. Cette eau s’évapore et se transforme partiellement en air, qui comprime la couche d’air et par contre-coup, la surface de la terre (60 b-d, 80 a) ; ainsi se forment, selon Platon, les différentes espèces de pierres dures ; l’étude des météorites n’a pas été abordée. Ces théories, reprises par Aristote[A 10], ont formé la base de la minéralogie et de la chimie jusqu’à l’époque moderne[118].
Le système planétaire selon Platon

Une fois l’Âme du monde constituée, le Démiurge a procédé à la construction de la sphère céleste ; l’univers du Timée se présente sous une forme exactement sphérique, car, « de toutes les figures, la sphère est la plus parfaite et la plus complètement semblable à elle-même » (33 b) ; contre Xénophane, Platon affirme la sphéricité de la Terre et du monde dans son ensemble, en se fondant sur la géométrie des Pythagoriciens et de Théétète ; après lui Aristote réaffirmera cette position dans son traité Du ciel[A 11],[119] ; cette sphère est divisée en quatre couches dont chacune est le lieu d’un des quatre éléments de la matière distingués par Platon, comme Empédocle l’avait déjà imaginé[120].
À l’aide de deux bandes croisées l’une sur l’autre, le Démiurge a formé les deux cercles concentriques de l’équateur céleste et de l’écliptique. Le cercle de l’équateur céleste, formé avec la substance du Même, correspond à la sphère des fixes, limite de l’univers ; celui de l’écliptique, formé avec la substance de l’Autre, correspond au plan orbital des planètes. Ces deux cercles tournent en sens inverse, « afin de sauver les apparences[121],[122] », selon la demande de Platon au mathématicien Eudoxe, chargé de le confirmer par ses calculs.
Platon énonce dans le Timée (39 a) plusieurs hypothèses astronomiques : la révolution des astres fixes dans le plan de l’équateur, la révolution en sens contraire des planètes dans le plan de l’écliptique, la vitesse respective de tous ces astres et leurs mouvements rétrogrades[123]. Il connaît leurs conjonctions (συνάψεις), les avances les uns par rapport aux autres (παραβολάς, προσχωρήσεις) ou le rebroussement de leurs orbites (ἐπανακύκλησις) (40 c)[note 9]. Mais il ne connaît pas les deux théories qui ne seront formulées qu’à l’époque d’Eudoxe pour expliquer ces phénomènes, à savoir la théorie des excentriques et la théorie des épicycles. Selon Francis M. Cornford, la description par Platon de son système planétaire fait référence à une sphère armillaire (σφαιρίον)[124] : le philosophe évoque lui-même « les modèles construits à l’imitation des phénomènes célestes » (40 d), qui existaient à l’Académie et chez les astronomes grecs de Syracuse[A 12].
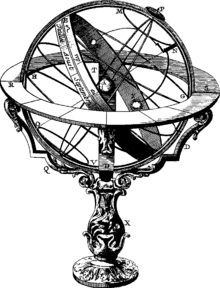
Dans cet univers, la Terre, selon la doctrine pythagoricienne, « a été faite pour être la productrice et la gardienne du jour et de la nuit » (40 b-c). Placée au centre du Monde[note 10], elle reste immobile[note 11] autour de l’axe qui traverse le Tout[125]. Autour de ce noyau central constitué par l’élément solide de la terre, s’étendent deux couches sphériques concentriques constituées l’une par l’eau, l’autre par l’air. Au-delà, s’étend la zone du feu, limitée extérieurement par la sphère des fixes[126].
Ainsi achevé, cet univers, « pourvu d’une Âme et d’un Intellect », offre quatre caractéristiques : la perfection mathématique du cosmos, sous le double aspect de la proportion continue et de la sphéricité ; l’unicité du monde ; son autarcie[127] ; et enfin sa santé et sa jeunesse éternelles (33 a)[128]. Pour apporter consistance et cohésion à ce système cosmique, Platon se réfère, dans ces postulats cosmologiques, à la force qu’Empédocle appelle Amitié (32 c) ainsi qu’aux arguments de Parménide relatifs à l’Un, et il s’oppose à la cosmologie atomiste de Démocrite qui postulait la pluralité des mondes[129]. Les derniers mots de Platon dans le Timée résonnent comme un hymne à la divinité de ce « Vivant parfait, formé de parties parfaites » (ζῷον τέλεον ἐκ τελέων τῶν μερῶν) :
« Vivant visible qui enveloppe tous les vivants visibles, Dieu sensible formé à la ressemblance du Dieu intelligible, très grand, très bon, très beau et très parfait, le Monde est né : c’est le Ciel qui est un et seul de sa race. (Timée, 92 c, trad. Albert Rivaud) »
Le Temps
Dans le Timée, Platon développe une théorie du Temps singulièrement moderne, peut-être empruntée aux Pythagoriciens[130],[A 13]. Le temps y est déterminé à la fois dans sa nature et dans sa fonction. La mise en ordre du monde sensible par le Démiurge se fait dans le temps, mais aussi conformément à la théorie des Formes intelligibles et immuables. Le Démiurge, fixant son regard sur le modèle éternel, a doté le monde d’un corps et d’une âme, et il s’est réjoui de le voir en mouvement et en vie ; sachant que rien d’engendré ne saurait être éternel, il chercha à rendre le monde encore plus semblable à son modèle noétique : « Alors il fabriqua une imitation mobile de l'éternité, cette image éternelle qui avance suivant le nombre (κατ’ἀριθμὸν ἰοῦσαν αἰώνιον εἰκόνα), et que nous appelons le Temps (37 c-d). » Le temps est l'image mobile de l'éternité immobile et une, et ce sont les mouvements des sept astres errants qui permettent de penser et de mesurer le temps[131]. Le temps en effet ne peut ni exister ni être pensé sans les mouvements du Soleil et de la Lune, et « né avec l'Univers, il se dissoudra avec lui, si jamais ils doivent se dissoudre. » (38 b) Platon distingue donc le devenir qui s’oppose à l’existence éternelle, et le temps, durée divisible et mesurable[132]. Or ce temps relatif que les hommes mesurent sur Terre n’est pas le même que le Temps cosmique en raison de ce que Platon appelle « la chorégraphie (χορείας) des planètes », avec leurs trajectoires « en nombre incroyable et de nature étonnamment variée » et leur mouvement prograde ou rétrograde[133] : il n’existe donc pas un temps mais plusieurs, tout aussi réguliers mais différemment rythmés[134]. Cette diversité de temps cosmiques est cependant enveloppée dans le temps unique qui, avec l’éternel retour de la Grande Année, ramène tous les corps célestes aux mêmes positions, et tous les temps au même[135].
Khôra, ou la théorie du lieu
Dans ce récit sur l’origine de l’univers, Platon a défini le Modèle intelligible, ainsi que la copie du Modèle — par comparaison, le père et l’enfant — mais sans jamais parler ni d’espace ni de matière ; or, la Nécessité, attachée de manière indissoluble à l’essence de tous les corps, impose d’ajouter une troisième sorte d’être, le « lieu » où adviennent les objets sensibles entrant dans le devenir[136]. Car il serait contradictoire ou que la copie fût son propre modèle, ou qu’une chose pût être dans une autre, qui en est différente, sans se confondre avec celle-ci ; il faut donc un troisième terme, un réceptacle où ait lieu la copie[137] : ce réceptacle, en grec ancien χώρα, « emplacement » / khôra, est une réalité difficile à définir selon Platon lui-même. Elle relève de la Nécessité, elle est indestructible, imperceptible par les sens (52 b) et précède l’ordre du monde instauré par le démiurge[138]. « Elle est une certaine espèce invisible et sans forme (ἀνόρατον καὶ ἄμορφον), qui participe de l’intelligible » (51 a-b) ; en tant que réceptacle universel (πανδεχής) qui reçoit tout ce qui se fait en elle, la khôra doit être vierge de toutes formes pour les recevoir toutes le mieux possible[139]. Avec une certaine insistance, Platon lui donne les traits de quelque chose de passif et de féminin : elle est assimilée à une nourrice et à une mère (μητέρα) ; elle est ainsi décrite à travers les images du « réceptacle » et de la « matrice » (49 a, 50 b-d)[140], autant de formules qui font penser à l’espace vide qui contient les objets visibles[141]. Mais Platon emploie aussi les métaphores du « porte-empreintes pour toutes choses » (50 e), de l’excipient désodorisé dans lequel les parfumeurs fixent les odeurs, et de l’or dans lequel le bijoutier façonne quantité d’objets : métaphores qui font songer à la matière. Or, « Platon n’a en vue ni l’espace ni la substance », écrit Albert Rivaud[142].
Les ambiguïtés prêtées à ce mot de khôra sont récentes[143] et ont soulevé des difficultés d’interprétation[note 12]. Quelle est la nature de la khôra, est-elle corporelle, ou abstraite et purement géométrique ? Dans l’antiquité, Aristote[A 14] tenait khôra pour un synonyme de ὕλη, la matière. Plotin, dans le traité 26 des Énnéades, Sur l’impassibilité des incorporels, y voit un non-être inétendu et informe. Son caractère amorphe implique en effet que la khôra n’est ni un corps[144] ni un matériau indéterminé[115]. Eduard Zeller y a vu quelque chose comme l’étendue cartésienne[145],[146]. En tant que lieu d’accueil universel, la khôra est la condition qui rend possible toute génération : or le lieu n’a pas de réalité propre. Martin Heidegger observe que les Grecs n’ont pas de mot pour « espace » : « Il ne faut entendre par khôra ni lieu ni espace, mais ce qui est pris et occupé par ce qui se trouve là »[147], de sorte qu’on distinguera « le lieu où se trouve et où est situé un corps (τόπος) et le fait que chaque réalité sensible possède en propre une place, la place qu’occupe une chose ou qu’elle abandonne en se déplaçant (khôra)[148]. » Ce réceptacle est défini par Léon Robin comme « l’emplacement éternel, χώρα ἀεί, le siège commun de tout ce qui, au cours de son devenir, occupe un lieu déterminé »[note 13],[132]. L’espace qui peut recevoir les copies des formes intelligibles n’est pas une substance nouvelle mais une composante essentielle dans l’analyse de ce qu’est un objet spatio-temporel[115] ; il représente une nécessité dialectique en offrant aux objets du monde sensible simplement l’occasion de s’étendre ; en somme, la khôra peut être assimilée au vide relatif des atomistes, mais à ceci près que de ce vide, ne subsiste rien d’inoccupé dans la cosmologie de Platon[149] : « un vide fugace, au-dedans d’un monde plein », résume Albert Rivaud[142]. Avec l’innovation importante que représente la khôra dans sa métaphysique, Platon reconnaît donc trois entités distinctes, antérieures à la génération du monde : l’Être, l’emplacement et le devenir, ὄν τε καὶ χώραν καὶ γένεσιν (52 d).
Physiologie, anatomie et médecine
L’anthropologie de Platon entreprend de décrire la nature du corps humain, à l’aide d’une physiologie fort rudimentaire et non dénuée d’obscurités et d’erreurs, fondée sur des connaissances « très imparfaites, beaucoup moins exactes et précises que celles des médecins, ses contemporains et ses devanciers », écrit Albert Rivaud[150] ; cette physiologie est centrée sur les deux fonctions intimement liées de la nutrition et de la respiration, la théorie de la circulation sanguine n’étant qu’ébauchée[151]. Le philosophe se distingue au contraire en élaborant une théorie, déjà très complète, de l’âme humaine et de son union avec le corps, la première « parmi toutes les doctrines qui domineront la philosophie, depuis Aristote, jusqu’à Descartes, Spinoza et Leibniz »[152].
L’âme immortelle et les âmes inférieures
Le Timée présente la doctrine platonicienne de l’âme sous la forme d’une synthèse entre l’ancienne croyance orphique ou pythagoricienne et la conception plus moderne de l’âme comme principe des fonctions corporelles[152].
En tant que principe de la vie, l’âme immortelle possède l’exclusivité de la double fonction, motrice et cognitive[153] ; elle est à l’origine de mouvements ordonnés en vue d’une certaine fin[note 14]. Tout ce qui se meut régulièrement de soi-même possède donc une âme[154] : c’est ce que Platon appelle dans le Timée « le principe immortel du Vivant mortel », ἀθάνατον ἀρχὴν θνητοῦ ζῴου (42 e) : façonnée par le démiurge lui-même, cette âme immortelle, unie au corps, demeure dans la partie la plus élevée de notre corps[155] : c’est pourquoi la tête est qualifiée de « demeure de ce qu’il y a en nous de plus divin et de plus sacré » (45 a). Constituée avant le corps, l’âme immortelle possède sur lui la maîtrise psychique : « C’est première selon la naissance et selon l’excellence que le Dieu constitua l’âme afin qu’elle commande et soit maîtresse du corps (δεσπότιν καὶ ἄρξουσαν) en le gardant sous sa domination » (34 c)[156]. Elle est un don de « Dieu qui en a fait cadeau à chacun de nous comme d’un génie divin » (δαίμονα) (90 a). Elle est en tout point semblable à l’Âme du monde, y compris pour les révolutions périodiques du Même et de l’Autre (43 a, 47 d). Dans son essence, Platon admet en effet ces deux révolutions, dans la droite ligne de la théorie de la révolution de l’âme exposée dans le traité Du Régime du corpus hippocratique[157] ; or, dans le désordre produit par les sensations, la première de ces révolutions est complètement entravée, et la seconde, troublée (43 c-44 a). Ce sont là les causes des illusions des sens, des erreurs et de la folie ; à la naissance, la déchéance de l’âme qui subit la loi de l’incarnation est si profonde qu’elle en perd d’abord la raison, elle devient folle[158] (ἄνους ψυχή)[A 15] jusqu’à ce que le sujet, « à mesure que le temps passe, et grâce à une bonne méthode d’éducation », acquière le bon sens (ἔμφρων)[A 16]. Platon recommande donc de se rendre, à force de contemplation, semblable à la beauté du monde et à l’harmonie des mouvements circulaires de l’Univers (90 c-d). La philosophie équivaut ainsi à une mise en ordre de l’âme, car celle-ci devient plus vigoureuse par l’exercice continuel des facultés les plus hautes de l’être humain, ses facultés intellectuelles et spirituelles[159]. Reconnaissant l’éminente dignité de cette âme immortelle et intelligente, Platon écrit :
« Par sa parenté avec le ciel, ce génie divin nous élève au-dessus de la terre, parce que nous sommes une plante non point terrestre mais céleste (φυτὸν οὐράνιον). Car de ce lieu d’où à l’origine a germé la naissance de l’âme, le Dieu tient suspendue notre tête, qui est notre racine (ῥίζαν ἡμῶν), et maintient ainsi droit tout le corps. (90 a-b)[note 15]. »
Par ses facultés supérieures, la pensée de l’homme est donc directement unie au divin, et par elle, notre salut (Platon dit σωτηρία, 88 b) nous appartient[160] ; en donnant la suprématie à l’intelligence, faculté par laquelle l’homme peut maîtriser ses passions, vivre une vie juste et atteindre à la réalité intelligible, Platon fonde une doctrine eschatologique de la connaissance[161].
Platon distingue également deux autres âmes, de nature mortelle, œuvres des dieux subalternes, et toutes logées au-dessous du cou (69 e) ; l’une, l’âme irascible, siège de la colère et de l’ardeur guerrière, ὁ θυμός (69 c-d), est dans le thorax ; l’autre, l’âme désirante, siège de l’appétit du boire et du manger, du plaisir et de la douleur, τὸ ἐπιθυμητικόν (70 d-e), est placée dans le ventre ; la violence des désirs dans « l’amour de la conjonction charnelle » (91 a) est présentée comme celle d’un être vivant animé, ζῷον ἔμψυχον, attaché à la génération[162] et absolument rebelle au raisonnement[163]. C’est de cette troisième espèce d’âme que sont aussi dotés les végétaux, qui, par leur passivité, appartiennent à une condition inférieure à celle de l’animal (77 b-c).
Maladies de l’âme et métempsychose
Comme le corps, l’âme a ses maladies, et Platon établit une relation de causalité entre dysfonctionnements physiques et troubles psychiques. La plus caractéristique de ces maladies de l’âme est la « déraison », (ψυχῆς ἄνοια, 86 b), perversion ou occultation de la rationalité qui peut prendre deux formes, la folie ou l’ignorance. Ces maladies peuvent résulter de plaisirs ou de douleurs excessifs qui affectent le corps avec violence et obscurcissent la raison et la connaissance[164] au point de provoquer, selon le cas, la peine, l’oubli, la mauvaise humeur, l’abattement, la témérité ou la lâcheté[165] ; « c’est la première fois, dans la littérature philosophique et médicale grecque, que la notion de maladie mentale est conceptualisée comme un trouble ayant des causes organiques qui affecte les capacités cognitives et comportementales d’un individu », observe Lucia Saudelli[166]. Inversement, une âme agitée, pleine d’une ardeur excessive, peut aussi rendre le corps malade et le consumer (87 e-88 a). Il est assez remarquable que pour Platon le déterminisme de ces psychopathologies ne soit pas simplement biologique mais aussi familial et social, l’éducation et l’environnement culturel et même politique (πολιτεῖαι κακαί, 87 b) jouant un rôle important. Ainsi, dans cette perspective psychosomatique, l’incapacité à dominer sa volupté et une « paillardise immodérée » sont des maladies de l’âme[165] ; selon Platon, celui qui tombe dans ces excès n’est pas vicieux volontairement, c’est un malade qui subit « l’effet de quelque disposition maligne du corps ou d’une éducation mal réglée » (86 e) : la doctrine socratique, « nul ne fait le mal volontairement »[A 17], est ici fondée sur des faits biologiques.
Contre les maux engendrés par les passions, leurs excès et les humeurs malignes qu’elles répandent dans le corps, Platon souligne la nécessité des rapports de proportion et d’harmonie qui doivent régir les parties du corps et de l’âme : en toutes choses, il faut préserver l’équilibre et la juste mesure, et « ne jamais mouvoir l’âme sans le corps, ni le corps sans l’âme. » (88 b) ; la thérapeutique platonicienne consiste donc en une éducation aussi bien physique qu’intellectuelle— au moyen d’études curatives[note 16], μαθήματα ἰατικά — [167]. Platon entremêle ainsi différentes traditions médicales : celle de l’école de Cnide qui prônait la primauté de la gymnastique et la nécessité d’un mouvement continuel, et celle de l’école pythagoricienne d’Alcméon de Crotone pour qui la santé était un équilibre[168]. Faute de quoi, celui qui s’abandonne entièrement à ses vices risque de « devenir mortel tout entier » (90 b)[note 17] et de connaître le cycle des métempsychoses[A 18]. Car, après la première incarnation de l’âme, d’autres incarnations se succèdent selon la manière, bonne ou mauvaise, dont la vie humaine aura été vécue ici-bas (42 b-d)[158]. Les âmes déchues peuvent alors se réincarner dans les corps de toutes sortes d’êtres vivants (91 d-e)[note 18], tandis que les pensées immortelles d’une âme vertueuse, appliquée à reproduire les harmonies du ciel, lui assurent l’immortalité. La psychophysiologie de Platon renvoie donc non seulement à sa cosmologie mais aussi à son éthique, dans une perspective eschatologique et sotériologique[169].
La théorie des sensations
En raison de ses conceptions finalistes (44 d-45 b), Platon expose sa théorie des sensations avant l’anatomie et la physiologie humaines. Pour rendre compte des impressions sensorielles (en grec ancien, αἰσθήσεις), il invoque les propriétés physiques des particules élémentaires du feu, de l’eau, de l’air ou de la terre, en particulier leur taille, leur forme et leur plus ou moins grande mobilité. La sensation est ainsi définie comme un mouvement d’incursion transmis de l’extérieur jusqu’à l’âme mortelle par l’intermédiaire de la chair (43 c) à l’aide des organes des sens conçus comme portes d’entrée du corps ; ce mouvement produit un ébranlement et c’est une information étrangère à la raison (45 d et 61 c). C’est ce mouvement d’incursion à l’intérieur qui explique le recours à l’étymologie platonicienne du mot αἴσθησις en grec, rapproché du verbe εἰσθεῖν, « accourir vers »[170]. Évitant les longs débats philosophiques sur les sensations qui avaient déjà eu lieu chez Alcméon, Empédocle, les atomistes, Antisthène ou Gorgias, et que lui-même avait traités dans le Théétète[A 19], Platon entend exposer ici cette théorie des sensations en naturaliste et en physicien[171], fidèle à la doctrine de l’intelligence de l’âme exposée dans le traité médical Du Régime du Corpus hippocratique[157].
La vision, les miroirs et les couleurs
La théorie de la vision proposée dans le Timée diffère de celle qui figure dans le Ménon (76 d) et qui remontait à Gorgias et sans doute à Empédocle[172]. Elle suppose trois sortes de feu distingués par Platon : le feu très pur et qui ne brûle pas contenu dans « les yeux porteurs de lumière » (φωσφόρα ὄμματα, 45 b) et qui s’en échappe en un flux continu ; le feu propre à chaque objet visible et qui se manifeste sous la forme de la couleur ; enfin, la lumière du jour, sans laquelle les objets restent en général invisibles (45 c)[173]. L’acte de la vision s’opère ainsi à l’extérieur de l’œil, dans ce que Platon considère comme « le corps de la vision », fusion entre le courant lumineux qui sort des yeux et la lumière diurne[172], sans qu’il soit jamais question de rayons ni d’un faisceau de lignes[174]. Les objets quant à eux laissent s’écouler des particules ignées qui, à la rencontre du corps de la vision, engendrent la sensation de la couleur (67 c-d)[175], la dimension de ces particules de feu étant compatible avec celle de l’orifice de l’œil afin de pouvoir y pénétrer[170]. La perception du noir et du blanc dépend respectivement d’un resserrement ou d’une dilatation du corps de la vision.

Platon nomme correctement quatre couleurs du spectre, le jaune, le rouge, le vert et le bleu, mais les mélanges des autres couleurs qu’il indique ne correspondent pas aux mélanges de lumières colorées de l’optique moderne (68 b-d) ; il semble plutôt songer aux mélanges des pigments colorés utilisés par les peintres et les teinturiers[176].
L’explication des images inversées dans un miroir manifeste la préoccupation de Platon pour cette notion d’image[A 20]. La remarque selon laquelle cette explication « n’est plus difficile à comprendre », laisse supposer que les miroirs suscitaient à son époque des tentatives d’explication[177]. L’image spéculaire, qu’il décrit comme « la production d’un simulacre » (εἰδωλοποιία) (46 a), ne repose sur aucune réflexion optique ni sur la vision binoculaire[176] : cette image, dotée d’une réalité d’imitation et localisée dans le miroir, résulte de la solidification unissant le corps de la vision et le flux de feu provenant du corps vu[178] ; la surface lisse du miroir sert de support à la rencontre et à l’union de ces deux feux[179]. Dans les miroirs concaves, Platon explique l’inversion de l’image par une réflexion non pas de la lumière mais du rayon visuel lui-même rebondissant sur la surface lisse[note 19] (46 c)[180] : il semble ainsi « avoir entrevu les principes d’optique géométrique à l’aide desquels on explique aujourd’hui l’inversion des images par le croisement des rayons[176]. »
Audition, goût, toucher et odorat
Le son est défini de façon remarquable : c’est « un choc (πληγή) transmis par l’air, à travers les oreilles, jusqu’au cerveau et jusqu’au sang, et qui se propage jusqu’à l’âme. » (67 b)[A 21]. Platon, comme Aristote[A 22], caractérise le son par les propriétés du mouvement qui le provoque, vitesse ou lenteur, uniformité ou incohérence, intensité plus ou moins grande, et il explique la cause de l’harmonie ou de la discordance des sons (80 a-b). Concernant le goût, il distingue sept saveurs fondamentales[A 23], expliquées tantôt par l’action mécanique des corps rugueux ou lisses, tantôt par leur action chimique, détersive et purifiante[181].
Au plan tactile, le feu donne une impression de chaud en raison de l’acuité de ses angles et de la petitesse de ses corpuscules qui lui confèrent une vive mobilité (61 e) ; l’impression de froid se produit quand, dégagés de l’humidité, les éléments les plus grands, ne pouvant entrer, poussent les plus hauts en cercle. « À cette lutte et à ces secousses, on donne les noms de tremblement et à la sensation celui de frisson » (61 e-62 b)[A 24]. Concernant l’odorat, il constate que toute odeur implique un processus chimique analogue à la fermentation ou à l’évaporation : toute odeur est donc l’état intermédiaire des corps en train de se transformer (66 d-e), c’est une fumée ou une vapeur[182]. Les corps élémentaires, en revanche, sont inodores. Théophraste dira que la bonne odeur est la suite de l’élaboration parfaite que la chaleur naturelle donne aux humeurs. Il attribue la bonne odeur à une sorte de coction des matières aqueuses, lorsque le principe humide, lequel est funeste, en a été dégagé par la chaleur.
Anatomie
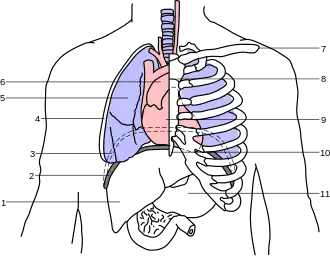
Le Timée contient un véritable traité d’anatomie, dans lequel Platon étudie les organes principaux (cœur, poumon, foie, rate, intestins et cerveau) et leurs fonctions ; le philosophe apparaît gêné par des connaissances anatomiques lacunaires et parfois imprécises[183], mais son but n’est pas médical ; il est de mieux préciser la situation des différentes espèces[note 20] d’âme[184] et leurs rapports avec le corps. L’anatomie, présentée constamment dans une perspective finaliste, apparaît ainsi comme une science annexe de la psychologie[185].
Le corps a été donné comme « véhicule » à l’âme immortelle[186]. Ce corps tout entier et ses processus physiologiques (circulation sanguine, nutrition, respiration) sont conçus pour permettre à l’âme immortelle-intelligente d’assurer sa domination sur les deux espèces mortelles que sont l’âme irascible et l’âme désirante[187] ; car toutes deux sont capables du meilleur comme du pire : ainsi, l’âme irascible, logée dans le thorax, entre le diaphragme et le nombril, peut-elle engendrer le courage, aussi bien que la fureur des désirs et de la colère ; mais celle-ci peut être ramenée à la raison grâce au cœur, « placé pour ainsi dire au poste de sentinelle » et source du sang qui circule dans tous les membres (70 a-b). De même, le foie, organe de l’âme désirante mais aussi de la divination (τὸ μαντεῖον), est-il en communication avec les images de l'intellect (71 b-72 c)[188] : tantôt l’intellect, avec ses pensées véhémentes, épouvante le foie, tantôt au contraire il libère la douceur que renferme le foie et rend ainsi joyeuse et sereine l’espèce mortelle de l'âme qui s’y trouve (71 b-d).
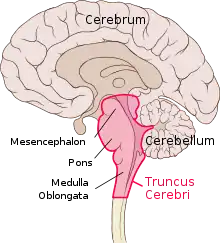
L’âme immortelle, pour maîtriser les mouvements corporels et remplir sa fonction, doit connaître tous les éléments dont le corps est composé et entrer en contact avec eux[189] ; or étant logée dans la tête, elle n’enveloppe pas la totalité du corps humain. Ce qui permet ce contact, et qui assure l’union intime[note 21] de l’âme et du corps auquel elle est liée « comme à partir d’ancres » (73 d), c’est une substance fondamentale, le principe à l’origine de tous les tissus, la moelle, (ὁ μυελός) sous ses trois formes : moelle du cerveau, (encéphale et moelle allongée), moelle spinale dans les vertèbres et moelle osseuse (73 b-74 a)[190]. Cette substance, composée des triangles « qui tiennent le premier rang pour la régularité et le poli », est à l’origine d’une « semence universelle pour tout le genre mortel » (πανσπερμία) ; mieux encore, la moelle contient toutes les sortes de figures que chaque espèce de corps doit avoir à sa naissance (73 c), c’est pourquoi Platon montre que tous les tissus organiques — os, chair, tendons, peau, ongles et système pileux — sont fabriqués à partir de la moelle[191], pressentant ainsi l’hérédité génétique[192]. Par sa configuration circulaire non seulement dans le cerveau « entièrement sphérique », mais aussi dans les vertèbres où elle présente une forme « ronde et oblongue », la moelle est soumise, comme il convenait, aux mouvements circulaires de l’âme, qui peut ainsi accomplir sa fonction[193]. Dans le même souci d’instaurer une continuité circulaire, Platon décrit, depuis la moelle jusqu’à la peau, aux cheveux et aux ongles, chacun des tissus biologiques enveloppant et protégeant celui qui le précède, le contient ou l’enferme, dans une progression continue du centre vers la périphérie du corps, les mouvements de circulation sanguine et de respiration étant eux-mêmes circulaires[194].
Pathologie et thérapeutique
Alors que l’Univers divin ne souffre pas de dépendance ou de vieillesse, l’organisme humain est sujet aux maladies ; selon Platon, celles-ci sont causées soit par une modification anormale de la proportion, de la situation ou des propriétés des éléments constitutifs du corps humain, soit par des désordres physiologiques particuliers[195]. Les causes de ces désordres sont un sang corrompu ou mêlé de sérosités (ἰχώρ), de toutes sortes de phlegmes (φλέγμα) ou d’humeurs peccantes telles que pituites. Suivant la doctrine hippocratique, Platon désigne ainsi diverses mucosités, glaire ou pus qui gâtent le sang, la chair, les os ou la moelle, et il leur donne le nom commun de bile (χολή), en distinguant bile jaune et amère, bile noire, bile rougeâtre et bile verte (83 b-84 c). Plusieurs maladies citées par Platon sont décrites en détail dans les livres du corpus hippocratique, mais le philosophe n’en énumère qu’un nombre extrêmement réduit : on a ainsi identifié la carie des os ou le cancer (84 b-c), le tétanos et l’opisthotonos (84 e), mais aussi l’épilepsie (85 b), les abcès ou phlegmons, les maladies inflammatoires, les diarrhées et les dysenteries (85 c-86)[196]. Le mal qui couvre le corps de taches blanches ou pituite blanche pourrait être la leucophlegmasie[A 25] ; les affections qui touchent les poumons sont vraisemblablement la congestion pulmonaire ou la bronchite (84 d-e). Les fièvres sont dites « continues, quotidiennes, tierces ou quartes » selon leur cause et leur durée. Cette pathologie platonicienne, très sommaire et assez incohérente[197], semble inspirée par des doctrines médicales diverses, où l’on reconnaît à la fois Alcméon, les Hippocratiques, et Empédocle[198].
Quant à la thérapeutique, Platon prône, comme les médecins de Cos, l’hygiène de vie (δίαιτα) par l’exercice harmonieux du corps et de l’esprit ; s’il n’exclut pas les remèdes de la pharmacopée (φαρμακευτικῆς ἰατρικόν), il les considère toutefois avec une certaine méfiance : « Jamais un homme de bon sens ne doit en faire usage sans nécessité » (89 b) car les maladies, ayant une durée définie, il ne faut pas « les irriter par des remèdes, quand elles n’offrent pas de grands dangers »[164].
Éthique et théologie de la volonté
Le but du thème traité dans le Timée, et annoncé d’emblée par Critias, était de rendre compte de la nature humaine dans le contexte de la nature de l’Univers, avant d’aborder la vertu humaine en action dans le dialogue suivant. Ce but est atteint à la fin du Timée : l’anthropologie s’achève en effet dans une psychologie morale et une éthique[199], qui permettent de définir les conditions du mode de vie le meilleur, en fonction de la nature rationnelle et immortelle de l’âme.
Hégémonie de l’âme rationnelle
Le concept platonicien d’âme humaine, dans sa divinité, implique un ensemble de prédicats qui l’associent à la raison et à une fonction d’hégémonie (ἡγεμονοῦν, 41 c)[200]. Dans la psychologie morale qu’il a esquissée, Platon accorde la priorité à la fonction de commandement dévolue à l’âme humaine dans sa relation au corps, en raison de sa « priorité d’origine »[A 26] : le Démiurge, en effet, « l’a faite plus ancienne que le corps par l’âge et par la vertu, pour commander en maîtresse (δεσπότιν καὶ ἄρξουσαν) et le corps pour obéir » (34 c). Cette fonction de commandement de l’âme est conçue par Platon comme une παιδαγωγία / paidagôgia[note 22] (89 d), l’exercice de l’art de « diriger, gouverner ». Pour permettre à l’âme rationnelle et immortelle d’exercer cette hégémonie, les hommes sont donc invités à cultiver soigneusement son bien-être, lequel consiste en un état « bien ordonné », εὖ κεκοσμημένον (90 c)[199]. Une âme est entretenue en bon ordre par « l’amour de la science et des pensées vraies », (φιλομαθία καὶ ἀληθεῖς φρονήσεις), ce qui est une des formes de la philosophie pour Platon, mais aussi par une sorte de spiritualité religieuse, c’est-à-dire « la capacité de penser aux choses immortelles et divines », φρονεῖν ἀθάνατα καὶ θεῖα (90 c) ; en particulier, il convient pour l’homme d’approfondir la connaissance de l’harmonie et des révolutions de l’Univers, et d’aligner sur elles les révolutions de l’âme humaine qui ont été troublées à la naissance[199]. Une fois réalisé, ce réalignement restaure l’âme à sa condition d’origine et apporte ainsi « l’achèvement de la vie parfaite offerte à l’humanité par les dieux, à la fois maintenant et pour toujours » (90 d). Seul ce culte rendu au génie divin (δαίμονα) qui habite en chaque être humain assure le bonheur et l’immortalité : c’est l’œuvre propre de l’âme humaine de permettre cette divinisation[200].
Théologie de la volonté
Cette doctrine de l’hégémonie est liée à la question de la causalité de l’âme, à la fois sur elle-même et dans le monde ; c’est dire qu’elle implique aussi la question de l’action et de l’intentionnalité. Or, le Timée a défini trois principes de commandement — le Démiurge, les dieux et l’âme immortelle —, et à l’hégémonie cosmique répond une hégémonie éthique ; l’Âme du Monde qui préside aux cycles du cosmos est relayée par l’âme humaine, dans son œuvre de divinisation. La volonté de l’Intellect divin, celle des dieux et de l’Âme du monde sont présentées par Platon dans un rapport d’imitation (μιμούμενοι τὴν ἐμὴν δύναμιν, 41 c)[200]. La volonté humaine est appelée elle aussi à reproduire par imitation, dans l’œuvre de divinisation, l’acte de la volonté du Démiurge[200]. Cette volonté démiurgique est intégralement bonne, (ἀγαθός / agathos) ; en ce sens la bonté absolue du dieu constitue pour Platon la cause première, « le principe essentiel du devenir et du monde »[201] ; cette bonté qu’il possède dans sa plénitude ontologique est aussi une bonté éthique qui meut la totalité de son vouloir[67] ; elle est dénuée de ce vice que les Grecs appelaient phtonos (φθόνος, 29 e), « envie »[A 27], qui caractérisait au contraire les dieux de la tradition, jaloux les uns des autres aussi bien que de la réussite éclatante des hommes[202]. L’absence de ce vice ou ἀφθονία définit une attitude vertueuse, qui agit comme une propension à la création, au don, à la générosité débordante : elle est à l’origine de la création de l’Univers dans le Timée, et caractérise la divinité, le philosophe authentique et l’amant véritable[203].
Les manuscrits du Timée
Le texte du Timée est connu par une trentaine de manuscrits dont le plus ancien est le Codex Parisinus græcus 1807 (A) conservé à la Bibliothèque nationale de France. Il a été écrit sur un parchemin de bonne qualité dans le troisième quart du IXe siècle, durant la période de renaissance byzantine qui a favorisé « la redécouverte, l’étude et l’imitation des œuvres littéraires de l’antiquité grecque »[204]. Il fait partie de la Collection philosophique dont l’origine généralement admise est constantinopolitaine[205]. Il a été découvert en 1490 et rapporté d’Orient par l’érudit byzantin Jean Lascaris[206]. Un second groupe de manuscrits, conservés à la Bibliothèque nationale autrichienne, à Vienne, comprend les Cod. Vindobonensis 21 (Y), 54 (W) et 55 (F). Les autres manuscrits sont le Cod. Palatinus Vaticanus 173 (P), conservé à la Bibliothèque Apostolique du Vatican[207], et le Cod. Parisinus græcus 1812 ; ce dernier, copié vers 1320-1330, est entré dans la bibliothèque de Colbert et faisait partie de la collection de manuscrits grecs accumulés par deux érudits français du XVIe siècle, Jean-Jacques de Mesmes et son fils Henri de Mesmes[208].
Réception et fortune du Timée
La réception du Timée à l’Académie de Platon

Le Timée n’a pas cessé d’inspirer philosophes et savants à travers l’histoire. Dans l’Antiquité, dès sa publication, l’ouvrage suscite d’intenses débats philosophiques[209] ; il occupe une place prépondérante au sein même de l’Académie de Platon où les disciples le tiennent pour l’œuvre capitale du maître[210] : Speusippe et Xénocrate en discutent de nombreux passages, et Crantor en rédige un commentaire. Au témoignage de Plutarque[A 28], jusqu’au Ier siècle av. J.-C., on interpréta la génération du monde par Platon comme une façon métaphorique de faire comprendre les éléments qui le constituent et le rapport entre la cause, les Idées et la matière ; cette interprétation était très répandue dans l’Académie ancienne, avec Speusippe et Xénocrate[211]. Aristote cependant est le premier partisan d’une interprétation littérale de la cosmogonie du Timée. La cosmologie du Stagirite dans son traité Du ciel prouve à quel point elle est redevable à celle du Timée, mais il s’y développe aussi une critique constante contre ce dialogue de Platon qui y est explicitement nommé[212]. Elle apporte ainsi quelques éléments d’information sur le monde de spéculations physiques et astronomiques que constituaient les discussions au sein de l’Académie[212].
Les questions se posaient parmi les philosophes et les astronomes grecs de savoir « si le cosmos a été créé ou non, et s’il est périssable ou indestructible »[A 29], si le monde est fini ou infini et s’il n’en existe qu’un seul ou une pluralité[212]. La critique qu’Aristote se soucie le plus de souligner, sans pour autant s’éloigner de Platon, c’est l’abandon du monde invisible des Idées érigé dans le Timée en modèle du cosmos visible, et la doctrine de la création de l’Univers par le démiurge[213]. La conception platonicienne d’un cosmos éternel (c’est-à-dire qui ne sera pas détruit en raison de la perfection de sa composition et de la volonté immuable de son auteur)[214] mais qui a eu un commencement, est rejetée par Aristote à la fois dans son traité Sur la philosophie et dans le premier livre Du ciel[A 30]. Pour lui, rien de ce qui est « engendré » ne saurait être « indestructible » ; par conséquent le monde n’a pas eu de naissance, il est un, éternel (c’est-à-dire sans commencement ni fin) et fini. Au Dieu-producteur platonicien, Aristote opposera plus tard un Dieu-générateur (γενέτωρ)[A 31] qui engendre la vie en vertu de la reproduction sexuée[215]. La théorie du mouvement circulaire continu que Platon attribue à la cause immatérielle de l’Âme du monde suscita également nombre de débats dans l’Académie. Les plus sérieuses objections vinrent des calculs nouveaux et précis entrepris par l’école d’Eudoxe et par Philippe d'Oponte sur la taille et la distance du Soleil, de la Lune et des autres corps célestes : ces calculs rendirent insoutenable la doctrine de la sphère du feu dans les cieux supérieurs, et ruinèrent en conséquence la théorie platonicienne de la transformation réciproque des éléments[212]. La volonté d’Aristote s’attacha dès lors à expliquer tous les phénomènes du mouvement par les lois naturelles de la matière, en élaborant une physique cosmique sans âmes des astres et sans interventions mythiques, non pas dans un esprit de polémique, mais afin de parvenir à une meilleure connaissance[212].
À la même époque, les stoïciens, Épicure, et les atomistes étudient le Timée et le commentent : grâce à ces philosophes, le Timée a contribué à maintenir l’intérêt pour les sciences du quadrivium durant toute l’Antiquité et au-delà[216].
La fortune du Timée
Les raisons de l’influence ininterrompue, voire de l’engouement suscité par le Timée sont en partie liées à la difficulté du texte, qui a pu laisser croire qu’il serait l’expression d’une sagesse mystérieuse et cachée, synthèse des connaissances des Pythagoriciens[217]. Elles tiennent aussi à son aspect d’encyclopédie, riche d’un savoir varié, qui a séduit les savants du Moyen Âge toujours soucieux de composer une somme des connaissances humaines, et qui a permis de féconder jusqu’à nos jours les domaines les plus divers de la philosophie et des sciences.
À l'époque du médio-platonisme
À l’automne 45 av. J.-C., Cicéron fait du Timée une traduction en latin dont il reste des fragments importants[A 32] ; cette traduction n’a exercé que peu d’influence, si l’on excepte la lecture qu’en a sans doute faite saint Augustin avant 400[218]. À partir du début du Ier siècle av. J.-C., une nouvelle forme philosophique se diffuse dans l’empire romain, celle de l’exégèse et du commentaire, qui permet de transformer les doctrines des dialogues de Platon en un système cohérent capable de rivaliser avec le stoïcisme et l’aristotélisme. C’est le Timée qui détient la prépondérance absolue dans l’exégèse médio-platonicienne, avec des Commentaires directs à ce dialogue ou des traités philosophiques portant sur un de ses thèmes, comme on le voit dans l’œuvre de Numenius, Sur le bien, ou le De Iside et Osiride de Plutarque[219]. Ce dernier en fait aussi un commentaire partiel dans son De animæ procreatione in Timæo Platonis, défendant l’interprétation littérale de la cosmogonie platonicienne. Parmi la quantité considérable d’œuvres exégétiques de formes diverses publiées à cette époque, on connaît les commentaires d’Atticus, de Sévère et de Taurus, ou les œuvres d’Harpocration et d’Albinus[219]. Auteur d’une Introduction aux dialogues de Platon ou Prologos, et d’un manuel intitulé Didaskalikos Logos, Albinus a joué, indirectement, un rôle important au siècle des Lumières, puisque son interprétation de la philosophie de Platon est celle qu’adopte d’abord l’historien allemand Johann Jakob Brucker et à sa suite, celle développée par Diderot et d'Alembert dans l’Encyclopédie : elle détermina ainsi l’idée que le XVIIIe siècle devait se faire de la philosophie de Platon[220]. À la fin du IIe siècle, le médecin Claude Galien étudie attentivement la partie du Timée consacrée à la physiologie et à la médecine ; il consacre à ce dialogue deux ouvrages, les Commentaires (Ὑπομνήματα) en quatre livres et une Synopse, que le syriaque Hunayn ibn Ishaq traduit partiellement au IXe siècle[221] ; Galien contribue ainsi à inspirer la médecine du monde oriental et du monde latin. Parmi les Alexandrins qui vouent un culte particulier au Timée, l’astronome et mathématicien Ératosthène propose une explication de la théorie de l’Âme du monde selon Platon[222].
Interprétations chrétiennes du Timée
Dès l’époque impériale romaine et jusqu’au début de l’Antiquité tardive, les débats sur la cosmologie sont largement déterminés par les commentaires du Timée. C’est l’un des dialogues de Platon les plus lus dans la patristique grecque, parfois par l’intermédiaire des auteurs juifs dont l’influence sur la lecture chrétienne de cette œuvre n’est pas négligeable[223].
Un passage du Timée (28 c), important pour les premiers chrétiens, était souvent cité, tant par des auteurs juifs comme Philon d'Alexandrie et Flavius Josèphe[A 33], que par des chrétiens comme Maxime de Tyr[A 34] : « Il est difficile, écrit Platon, de découvrir l’auteur et le père de cet Univers, et quand on l’a découvert, il est impossible de le divulguer à tous ». Cette formule est considérée par les philosophes du moyen-platonisme puis de l’Antiquité tardive comme le témoignage de la nature inconcevable et ineffable de Dieu ; cette exégèse traditionnelle mais à contresens a ensuite été reprise par plusieurs auteurs chrétiens. Selon le mot de Sébastien Morlet, « la lecture chrétienne de ce texte illustre parfaitement la réception ambivalente de Platon dans le christianisme ancien, tantôt loué pour s’être approché de la vérité et tantôt dénoncé pour ne pas s’en être assez approché[224] ». Pénétré de platonisme, Clément d’Alexandrie proclame la nécessité de la culture grecque ; il en adopte le programme d’éducation, l’idéal moral et la dialectique, en accordant à la philosophie grecque une importance égale à celle des Écritures de l’Ancien Testament et il justifie cette conviction par l’idée que les philosophes ont pillé l’enseignement de Moïse et des prophètes[225]. D’une manière générale, les savants chrétiens s’attachent avec ardeur au Timée[210] : parmi les Pères de l'Église, ce sont notamment Basile de Césarée et Grégoire de Nysse qui y découvrent en germe le dogme de la Trinité[226]. L’hypothèse, formulée par Platon, de l’origine du monde qui serait né (γέγονεν, 28 b) est interprétée dans le sens du récit biblique de la Création ex nihilo[223]. Le Livre de la Genèse et le Timée, rapprochés par Eusèbe de Césarée et les Pères de l’Église, sont dès lors comptés au nombre des ouvrages fondateurs de la pensée occidentale[4].
Du néoplatonisme au Moyen Âge

Dans l’Antiquité tardive, Plotin (205-270) se donne pour tâche de reprendre tous les enseignements de Platon pour les expliquer à ses disciples, et ses traités portent la marque d’une profonde influence du Timée ; mais il n’hésite pas aussi à attaquer la conception du démiurge de Platon vu comme un artisan, à en répudier d’autres, et à élaborer ainsi sa propre doctrine en cosmologie, en psychologie et en métaphysique : il devient le fondateur du néoplatonisme[227]. Son élève, Porphyre, auteur d’un Commentaire au Timée, joue un rôle fondamental comme source de Proclus pour son propre Commentaire sur ce dialogue[228]. Proclus se réfère aux lectures d’Albinus, de Plotin, de Porphyre, de Syrianos et d’Atticus, mais aussi au Commentaire de Jamblique. Tenant compte des désaccords interprétatifs entre tous ces philosophes, il étudie en particulier le débat qui portait sur le statut ontologique du Démiurge, son rapport avec les Idées et leur produit ; la question de savoir si le Démiurge existait aussi avant le moment de la création soulevait la thèse d’un temps pré-cosmique[229]. Grâce au Timée et au Parménide, Proclus va réaliser la synthèse de ces questions métaphysiques qui ont agité le néoplatonisme tardif, en inaugurant une création originale, « ce qu’il faut bien appeler la théologie comme science », selon le mot de Luc Brisson[230].
Aux VIe et VIIe siècles, le Timée de Platon est connu grâce à la traduction latine effectuée par Chalcidius vers la fin du IVe siècle : des copies de cette traduction sont attestées en Gaule-Francie et en Hispanie[231]. Dès l’époque carolingienne, c’est dans cette traduction latine de Chalcidius, seul texte alors accessible, que le Timée est étudié dans l’Occident médiéval ; bien que partielle (elle couvre seulement les lignes 27 à 53 c), elle est accompagnée d’un riche commentaire visant à éclairer ce texte difficile. Elle se diffuse dans plusieurs centres monastiques, comme l’abbaye bénédictine de Fulda en Allemagne, ou l’abbaye de Fleury dans le Val de Loire ; elle est connue des grands intellectuels qui fréquentent le cercle d’Alcuin, le savant directeur de l’École palatine à Aix-la-Chapelle, ainsi que des philosophes Jean Scot Érigène et Gerbert d’Aurillac, futur pape sous le nom de Sylvestre II[232]. Le passage du Timée (35 b-36 b) relatif à la création de l’âme du monde construite selon des rapports musicaux est utilisé conjointement avec le traité de l’Institution musicale de Boèce. Les savants médiévaux sont ainsi conduits à concevoir la notion de musique des sphères : elle intéresse non seulement un théoricien de la musique comme Hucbald de Saint-Amand mais elle engage même les musiciens médiévaux à faire coïncider leur pratique avec la théorie platonicienne, grâce à l’adoption d’une échelle musicale constituée sur le modèle des diagrammes établis par Chalcidius : « Elle sera utilisée dans toutes les mesures d’organistrum, dans les mesures de tuyaux d’orgue et parfois dans les mesures de cloches »[233].
Aux XIe et XIIe siècles, les savants et les théologiens juifs, musulmans et chrétiens, en particulier les théologiens de l’École de Chartres commentent le Timée d’après cette traduction latine de Chalcidius, et le citent[226]. Les philosophes chartrains essaient de concilier la cosmogonie du Timée avec le Livre de la Genèse. Ils sont particulièrement intéressés par la notion de cosmos, cette harmonie de la nature — où ils voient une iustitia naturalis — qui doit servir de modèle pour établir la paix dans l’âme humaine et dans la société[234] — la iustitia positiva —. Mais la faveur dont jouissent les conceptions de Platon sur la nature, inconnues des Pères de l’Église, inquiètent certains théologiens comme Adalbold II d'Utrecht et Manegold de Lautenbach : bien que sans parti-pris contre le philosophe grec dont ils reconnaissent les mérites, ils redoutent l’idée d’une physique païenne, soustraite à l’influence de l’Évangile, et qui prétendrait expliquer rationnellement l’origine de l’homme et du monde[234]. À Chartres, où fleurit le culte de Platon, le maître Guillaume de Conches commente systématiquement la traduction de Chalcidius, en particulier pour le domaine arithmétique et musical[235]. Il rédige des Gloses sur le Timée, où il élabore une herméneutique et propose un parallèle entre l’Âme du monde selon Platon et le Saint Esprit, ajoutant prudemment à propos du philosophe grec : « Si l’on considère, au-delà des mots, la pensée même de l’auteur, non seulement on ne trouvera pas d’hérésie, mais on découvrira une très profonde philosophie cachée sous l’enveloppe des mots[236] ». C’est encore à la cosmologie du Timée et à la doctrine platonicienne des Idées qu’il faut se référer si l’on veut comprendre la position d’un autre maître, Bernard de Chartres, et celle de Pierre Abélard sur le problème des universaux[237]. L’argumentation d’Abélard atteste qu’il connaît le démiurge du Timée, la conception platonicienne de l’Intellect et la théorie des formes à travers la présentation qu’en a donnée Macrobe dans son Commentaire au Songe de Scipion. Sa théologie chrétienne, où la notion de Souverain Bien occupe une place centrale, est toute imprégnée de platonisme ; pour avoir voulu expliquer rationnellement le mystère de la Trinité, et avoir voulu soumettre la religion et la morale à l’exercice de sa puissante dialectique plutôt qu’à la foi, Abélard est finalement condamné en 1140 au concile de Sens[238].
Durant les deux siècles suivants, tenus pour l’âge des ténèbres en matière d’hellénisme, la référence à Platon ne se rencontre plus que chez de rares lettrés comme Albert le Grand ou le poète Dante. Au chant IV du Paradis[239], l’auteur de la Divine Comédie, s’interroge sur la doctrine platonicienne de l’âme humaine et le séjour des Bienheureux. Quelle est la signification de ces « âmes semées dans les instruments du Temps » par le démiurge, dont parle Platon dans le Timée[A 35], et qui, après leur mort, retourneraient dans les astres, après une vie vécue ici-bas dans la justice ? La voix de Béatrice suggère au poète que peut-être, il faut entendre Platon non dans un sens littéral mais dans un sens métaphorique. Elle lui enseigne que « mal entendu, ce principe [i.e. de Platon] égara presque tout le monde » qui y vit les divinités nommées Jupiter, Mercure et Mars[240].
Influence dans les temps modernes
Au XVe siècle, une délégation byzantine venue de Constantinople en Italie pour participer au concile de Florence-Ferrare en 1437 suscite un intérêt accru pour l’œuvre de Platon et particulièrement pour le Timée dont la doctrine « rencontrait manifestement les aspirations de bon nombre d’esprits déconcertés par un contexte culturel, politique et ecclésial difficile »[241]. On le constate dans les œuvres de deux des participants à ce concile, Gémiste Pléthon et Nicolas de Cues. Pléthon défend résolument la supériorité de la conception platonicienne de Dieu, de la genèse du monde et de la cosmologie mathématique du Timée, jugées nettement supérieures théologiquement à la conception aristotélicienne[241]. Nicolas de Cues estime lui aussi que les conceptions développées dans le Timée peuvent s’accorder avec le christianisme, moyennant certaines adaptations doctrinales : le livre de la nature est bien écrit en langage mathématique, et grâce aux arts libéraux du quadrivium, l’homme a la capacité de comprendre en partie les relations entre les choses, même si Dieu seul possède la clef définitive de l’Univers[242]; dans son ouvrage, La Docte Ignorance, Nicolas de Cues récuse la doctrine platonicienne des trois principes de l’acte créateur — démiurge, modèle intelligible, matière primordiale informe — au profit de la Trinité, en qui se rassemble toute la causalité de la création ex nihilo. Il rejette également la théorie de l’Âme du monde, incompatible avec sa propre conception d’un univers infini (le centre est partout, la circonférence nulle part), et indéfini (c’est-à-dire non doté d’une forme)[243].
L’intérêt pour le Timée s’accroît bientôt grâce au travail de l’humaniste florentin, Marsile Ficin, qui rédige en 1483 et 1484 un Commentaire sur le Timée (Compendium in Timæum) avec, pour la première fois, la traduction intégrale de ce dialogue en latin[244]. Dans l’interprétation de Ficin, la figure centrale du démiurge donne sens à la théorie de l’homme créateur complétant l’œuvre divine ; cette synthèse unique entre la pensée médiévale, l’héritage religieux et le platonisme grec, exerce une influence considérable et devient l’interprétation définitive adoptée par la Renaissance. Dans cette traduction latine qui occupe une place de choix dans la bibliothèque des clercs, le Timée influence alors toute la culture occidentale, alimentant les débats théologiques sur le Verbe incarné, l’immanence au monde et la transcendance de Dieu[245]. Astronomes et mathématiciens tâchent de pénétrer le sens caché des passages relatifs à l’Âme du monde[217].

C’est bientôt dans le texte original que les savants vont lire le Timée dont la première édition en grec est publiée en à Venise, grâce au travail attentif de l’érudit crétois, Marcus Musurus, ami de Jean Lascaris.
À la fin du XVIe siècle, le fondateur de l’astronomie moderne, Johannes Kepler, est influencé par la cosmologie et la physique mathématique du Timée, de même que Galilée[246] et Descartes dont la pensée présente bien des analogies avec celle de Platon[247] ; en , Leibniz lit et médite le Timée, tandis que, jusqu’au XVIIIe siècle, des savants essaient même de localiser l’Atlantide[248]. En France Voltaire, hermétique à toute spéculation cosmologique et métaphysique, présente le philosophe grec, dans le conte intitulé Songe de Platon, comme un rêveur de théories fumeuses.
En Allemagne, l’influence du Timée s’exerce sur nombre d’érudits, de philosophes et de philologues. Parmi ces philosophes, Schelling puise très tôt dans l’œuvre de Platon auquel il doit beaucoup, et dont il emprunte encore la dialectique dans ses dernières œuvres ; selon le mot de Xavier Tilliette, le Timée est « le dialogue platonicien sans doute le plus fascinant pour Schelling »[249]. En -, le jeune Schelling n’a que dix-huit ans lorsqu’il lit intensément le Timée dans le texte, le traduit, et rédige son propre commentaire au dialogue de Platon sous le titre Timæus. Ce commentaire porte sur la seule section allant de 27 d à 53 b, la partie qui expose la genèse de l’univers[250] ; Schelling s’intéresse en particulier aux trois entités platoniciennes des Formes intelligibles, des choses sensibles et du réceptacle. Il donne du Timée une interprétation historiquement très orientée, dans la ligne de l’idéalisme transcendantal de Kant, et des débats post-kantiens : la relation entre l’Intellect et la Nécessité de Platon apparaît à Schelling comme la relation de la forme et de la matière de la connaissance[251] ; la mise en ordre du chaos originel par le démiurge est conçue comme « l’opération de l’intellect qui unifie le divers de l’intuition dans l’unité d’une représentation[251] ». Schelling n’a donc pas eu pour objectif d’expliquer le Timée ou de faire comprendre Platon pour lui-même, mais plutôt d’accumuler des notes de lecture pour nourrir sa propre réflexion, sur un texte considéré comme fondateur de l’histoire de la philosophie[252].
Au début du XIXe siècle, les philosophes allemands débattent de la doctrine de Platon sur le fond. En 1804, le philosophe Karl Joseph Hieronymus Windischmann publie sa traduction du Timée, où il voit « un authentique document de la vraie physique, et une œuvre splendide sur la nature des choses[253] », tandis que Johann Friedrich Herbart, dans son essai De Platonici systematis fundamento commentario publié un an plus tard, rejette vivement cette présentation élogieuse, allant jusqu’à dénier toute valeur moderne à ce dialogue[254]. Dès 1804 Tennemann, très bon connaisseur de Platon, lui consacre une monographie de 1 200 pages et apporte la démonstration irréfutable du caractère apocryphe du Timée de Locres ; mais les philosophes Schelling[226] et Hegel admettent encore l’hypothèse dépassée selon laquelle le dialogue de Platon serait « l’élaboration d’une œuvre conçue en propre par un Pythagoricien »[255]. Les savants Friedrich August Wolf et August Böckh étudient les problèmes philologico-historiques soulevés par la composition du Timée[256]. Quelques années plus tard, s’intéressant à son tour au Timée, Friedrich Nietzsche formule l’hypothèse que Platon a incorporé ou retravaillé l’Hermocrate et l’a ajouté aux textes des Lois[257].
Sur le plan philosophique, c’est sur Hegel que l’influence du Timée apparaît la plus forte. Il retient du Timée les questions qui sont, selon ses propres mots, « la base fondamentale » (die Grundlage) : la conception de Dieu, la proportion, la notion d’âme, la valeur du monde, le problème du temps et de l'espace[254]. Il reconnaît que Platon a eu, comme les néoplatoniciens, l’idée exacte de la vraie nature de Dieu et la prescience claire de la Trinité chrétienne[258]. Le concept platonicien d’âme du monde est à l’origine chez Hegel de la notion d’Esprit existant dans le monde ; elle signifie pour lui la supériorité de l’Esprit sur la matière[259] ; par son statut intermédiaire que Hegel a bien perçu, l’âme du monde représente l’intelligibilité du monde divin qui lie le Dieu trine à la nature multiple[260]. Il reconnaît aussi sa dette envers Platon sur l’idéalité du Temps et de l’espace qui ne peuvent être compris par rapport à la matière mais seulement par rapport au monde divin[261].
Au XXe siècle, Jacques Derrida constate le paradoxe et l’énigme que représente la khôra platonicienne : ce troisième genre d’être ne peut être approché que par « un raisonnement bâtard », constatait déjà Platon (52 b). La khôra a obsédé Jacques Derrida depuis quasiment le début de son travail, dans La Pharmacie de Platon en , jusqu’à la fin, dans Voyous publié en , quelques mois avant sa mort[262]. Il traite de cette notion de manière approfondie dans Comment ne pas parler (Psyché, ) et Khôra (). Dans cette dernière œuvre, il insiste sur la nécessité de « laisser le nom de khôra à l’abri de toute traduction » et de supprimer l’article défini qui « présuppose l’existence d’une chose, l’étant khôra, auquel, à travers un nom commun, il serait facile de se référer[263]. » En , la comparaison, faite par Platon, de la khôra avec le tamis de vannage de l’agriculteur devient le motif central d’une correspondance entre le philosophe et l’architecte Peter Eisenman à propos d’un projet qui avait précisément pour nom Choral Work. Faisant allusion à cette comparaison, Derrida avouait son aporie : « Ce passage est dans le Timée aussi erratique (me semble-t-il), difficilement intégrable, privé d’origine et de telos manifeste que cette pièce que nous avons imaginée par notre Choral Work[264]. »
Philosophes et scientifiques du XXe siècle
Au XXe siècle, sept personnalités de premier plan, versées à la fois en philosophie, en mathématique, en physique théorique et quantique, ont montré à quel point les intuitions du Timée de Platon pouvaient inspirer leurs propres travaux, et même servir l’unité de la connaissance.
En , le mathématicien, logicien et métaphysicien Alfred North Whitehead déclare que le Timée revêt la même importance scientifique que le Scholium ajouté par Isaac Newton, en , à ses Principia[265] ; ces deux ouvrages, le Scholium et le Timée, constituent les plus grands textes cosmologiques[42], et sont aussi « ceux qui ont exercé l’influence la plus profonde sur la pensée occidentale »[266]. Le paradoxe de ce jugement s’explique : la physique du XXe siècle, relativiste et quantique, accorde en effet un nouveau rôle aux nombres entiers en raison du quantum d’action mécanique de Planck : à l’opposé du calcul différentiel et intégral de Leibniz et de son célèbre « Natura non facit saltus », la physique quantique introduit une sorte de nouveau pythagorisme[267], après celui qui a inspiré Platon[note 23]. Whitehead reconnaît la vitalité de la philosophie platonicienne en général et l’importance capitale de sa contribution à l’histoire de la pensée occidentale. Dans sa « philosophie du processus » (en anglais : Process Thought), les axes majeurs de son propre système que sont « Dieu, les Objets éternels, la Créativité », sont explicitement mis en parallèle, respectivement avec les concepts platoniciens du Démiurge, des Idées, et de la Khôra (ou réceptacle), présentés dans le Timée[268].
Le lauréat du prix Nobel de physique et l’un des fondateurs de la mécanique quantique, Werner Heisenberg, lit le Timée quand il fait son service militaire à Munich[42]. Dès , il publie un article sur la philosophie grecque, approfondissant le monde des Idées de Platon et puisant quelques réflexions chez les présocratiques[269] ; dans ces sources antiques, il recommande de « prendre aux Grecs leur principe de pensée et leur façon de poser la question de principe. À l’origine de la culture occidentale, écrit-il, on trouve cette relation étroite, établie par les Grecs, entre l’énoncé du questionnement à partir des principes et la pratique empirique[270] » ; il met aussi à profit la notion aristotélicienne de puissance, et rejoint Platon dans sa modélisation mathématique des corpuscules élémentaires : « Les particules élémentaires dans le Timée de Platon, sont finalement non de la substance mais des formes mathématiques. La formule “Toute chose est nombre” est attribuée à Pythagore. Les seules formes mathématiques dont on disposait à l’époque étaient des formes géométriques comme les solides réguliers ou les triangles définissant leur surface ; en théorie quantique actuelle, il ne peut y avoir de doute que les particules élémentaires seront également pour finir des formes mathématiques[271]. »
Entre et , le mathématicien et philosophe Albert Lautman, « un des philosophes les plus inspirés de ce siècle », selon le mot de Jean Petitot[272], veut construire une philosophie des sciences directement métaphysique. Il est authentiquement platonicien dans sa conception de la participation du Sensible à l’Intelligible et sa référence immédiate aux Idées ; pour lui, « le rapprochement de la métaphysique et des mathématiques n’est pas contingent mais nécessaire[273]. » L’être mathématique, écrit-il, « n’est pas sans analogie avec un être vivant[274] », et les théories mathématiques et physiques sont comme des structures organisatrices douées d’harmonie, d’autonomie et de vie. Les créations mathématiques doivent être lues, selon lui, comme des approfondissements d'oppositions dialectiques au sens platonicien entre des contraires tels que le Même et l'Autre, le Continu et le Discontinu, l'Essence et l'Existence, le Fini et l’Infini[275]. « Les théories mathématiques participent à une réalité idéale qui est dominatrice par rapport à la mathématique. » Mais ces Idées « ne sont pas des modèles dont les êtres mathématiques ne seraient que des copies »[276], précise-t-il ; à la différence de Platon, Lautman supprime en effet la distance irréductible qui sépare l’eidos (εἶδος, « Forme, Idée ») de sa représentation, pour affirmer le pouvoir producteur des idées qui s'incarnent dans les théories[277] : « La nature du réel, sa structure et les conditions de sa genèse ne sont connaissables qu’en remontant aux Idées, dont la science incarne les liaisons[278]. »
Dans une étude publiée en et intitulée Symmetry, le mathématicien et physicien Hermann Weyl constate la justesse des intuitions exprimées par Platon dans le Timée sur les propriétés mathématiques de la matière : « Je suis enclin à penser, avec Platon, écrit-il, que les lois mathématiques qui gouvernent la nature sont à l’origine de la symétrie dans la nature, et que la perception intuitive de cette idée dans l’esprit des artistes, est son origine dans l’art[279]. » Il ajoute que parmi les cinq polyèdres réguliers de Platon, « la découverte des deux derniers [dodécaèdre et icosaèdre] est certainement l’une des plus belles et des plus extraordinaires découvertes qui aient été faites dans toute l’histoire des mathématiques[280] » ; le Timée anticipe en effet un concept moderne et abstrait, puisqu’il présente déjà « un ancêtre antique de la structure de groupe »[267], en raison du rôle des rotations imprimables aux polyèdres réguliers[281].
La philosophe Simone Weil, tout en participant aux réunions du groupe Bourbaki et en s’intéressant à la théorie des quanta[282], lit et commente le Timée : elle s’inscrit dans la longue tradition de ceux qui, des Pères de l’Église à Abélard, et jusqu’à Hegel y ont découvert le mystère chrétien de la Trinité[note 24]. Elle résume en ces termes sa lecture chrétienne du Timée : « Cet être que Platon nomme l’Âme du Monde est le Fils unique de Dieu ; Platon dit monogenès (μονογενής, 31 b) comme saint Jean. Le Modèle à la ressemblance duquel l’Âme du Monde est engendrée est un vivant spirituel, ou un esprit vivant (ζῷον ἔμψυχον, 30 b). C’est donc une personne. C’est l’esprit absolument parfait à tous égards. C’est donc Dieu. Il y a donc trois personnes divines, le Père, le Fils Unique et le Modèle. Dès qu’on remplace modèle par inspiration, la convenance de cette image appliquée au Saint-Esprit est évidente »[283]. Sa conception du rôle médiateur du Beau dans la contemplation de l’ordre divin du cosmos[284] s’inspire de la création du monde par le démiurge contemplant un modèle : par analogie avec la création artistique, où « il y a finalité sans aucune fin représentable », elle développe une métaphysique du détachement et du renoncement à toutes les fins[285]. Simone Weil reprend également à Platon la notion-clef de « proportion géométrique » (31 c) à laquelle elle donne, « en plus de son sens visible un sens théologique », celui du Christ auquel saint Jean donne le nom de Logos, terme qui désigne en grec le Médiateur ou la moyenne proportionnelle[286]. L’influence de Platon sur Simone Weil s’avère forte, particulièrement sur sa conception du Temps et du moi[287]. Conformément à cette idée essentielle du Timée que nous devons reproduire en nous l’ordre du monde et l’harmonieuse circularité de son mouvement, elle pense l’arrachement au devenir ; par la régularité de leurs retours, les corps célestes symbolisent « l’équivalence de l’avenir et du passé, et, si nous contemplons en eux cette équivalence, étant délivrés du désir tourné vers l’avenir, nous le sommes aussi de l’imagination qui l’accompagne, et qui est l’unique source de l’erreur et du mensonge »[288]. Dans le Timée, ce « dialogue qui ne ressemble à aucun autre », Simone Weil découvre au total une conception mystique de la connaissance : Platon ayant contemplé l’univers comme Dieu le voit, a essayé de l’expliquer aux hommes ; « Platon, écrit-elle, est sorti de la caverne, il a regardé le soleil, et il est rentré dans la caverne »[289].
Carl Friedrich von Weizsäcker, professeur de physique théorique, spécialiste de l’atome, en même temps que professeur de philosophie, s’intéresse à la philosophie de la nature ; en 1970, dans une conférence intitulée « La science platonicienne dans l’Histoire », il constate que la physique moderne semble récapituler les idées de Platon mais avec une conception différente du Temps. Le système des particules élémentaires du Timée, qui sont constituées sur la base des triangles et de la ligne, ramène à une modélisation mathématique et implique le principe d’unité de la nature comme dans la physique moderne. Pour Weizsäcker, les développements futurs de la physique moderne exigent une réflexion philosophique qui devra prendre en considération la pensée de Platon « en tant que partenaire »[290].
En 2010, le physicien Anthony Leggett, lauréat du prix Nobel de physique de , publie un essai sur les Résonances du Timée de Platon dans la physique et la cosmologie modernes[291]. Il y affirme que Platon pose les bonnes questions sur la naissance de l’univers et sur les rapports du Temps et de l’univers ; les relations que Platon établit entre la Nécessité, l’espace et l’Intellect illustrent un débat toujours actuel : faut-il concevoir cet univers comme le résultat des constantes de la physique, ou comme le résultat de conditions initiales arbitraires ? Anthony Leggett constate aussi que l’exposé de Platon sur la structure des particules élémentaires demeure jusqu’à nos jours riche de suggestions et susceptible d’inspirer la pensée contemporaine.
Notes et références
Notes
- La description de cette cité idéale rappelle de près celle qui a été présentée dans La République.
- Martin L. West souligne que Platon offre une courte théogonie (40 d) dans le Timée, parlant de « progénitures des dieux » ; cette théorie rapportée par Platon est d’après lui de Musée d'Athènes ou Orphée.
- Platon, Philèbe, 28 c : Νοῦς βασιλεὺς οὐρανοῦ τε καὶ γῆς, « Intellect roi de notre univers » ; La République, VI, 509 b.
- Divers commentateurs ont proposé d’identifier ces deux essences primitives ; seule l’identification du Même et de l’Autre respectivement à l’Intelligible et au Sensible est généralement admise, malgré les difficultés qu’elle soulève ; elle est admise entre autres par les philosophes Jean-François Pradeau (op. cit., p. 491), Albert Rivaud (op. cit., p. 41) et Léon Robin (op. cit. p. 287) ; ce dernier précise : « Le Même absolu, c’est l’indivisibilité de l’unité pure, l’Autre absolu, c’est la divisibilité infinie de la pure multiplicité, en particulier des corps dans le devenir. » Certains mathématiciens ou historiens des sciences proposent de concevoir ces notions en termes mathématiques : Bernard Vitrac (op. cit., p. 37) parle de l’opposition de l’Égal et de l’Inégal. Georges Kayas (op. cit., pages 295-296) identifie la substance fixe qui ne varie jamais, à l’unité ; la substance divisible est identifiée avec le nombre 2 ou dyade, en tant que principe de différenciation et de dichotomie ; la tierce substance serait le nombre 3, mélange difficile du pair et de l’impair. En ces matières difficiles, il semble vain d’exiger de Platon une impossible précision en discours rationnel, tant chez lui « intuition esthétique, découverte scientifique et extase religieuse » se mêlent intimement, selon le mot de René Schaerer (La question platonicienne, Paris, Vrin, 1938, p. 260).
- Dans son Traité sur la création de l’âme d’après le Timée de Platon, Plutarque développe les principes d’après lesquels Platon a voulu expliquer la formation de l’Âme du monde. Les astres eux-mêmes ont une âme (38 e).
- Modalités de la médiété à 3 termes, A-M-B, où la relation de A à M est la même que celle de M à B : Médiété arithmétique = la relation de A à M est la différence A − M. Médiété géométrique = la relation de A à M est la division de A ÷ M. Médiété harmonique = la relation de A à M est la portion de A que représente la différence A − M.
- Cette conception serait assez proche de celle du mazdéisme selon Jean Haudry (Le feu dans la tradition indo-européenne, Archè, Milan, 2016, p. 113).
- Platon omet-il volontairement ou non les surfaces courbes ? Cette question a été examinée chez plusieurs commentateurs comme Francis M. Cornford, Thomas-Henri Martin (lire en ligne, Vol. 2, p. 235 sq.), John Burnet, Léon Robin (op. cit., note 1 p. 267) et Arnaud Macé (op. cit., note 58 p. 113).
- La παραβολή serait la différence de latitude ou de longitude entre deux astres qui se lèvent et se couchent à peu près au même moment, comme Vénus et le Soleil. La προσχώρησις serait l’avance d’une orbite par rapport à une autre.
- Outre sa signification astronomique, le géocentrisme signifiait aussi que « la Terre, comme l’homme de Protagoras dans le monde moral, était la mesure de toutes choses dans l’univers cosmologique. » (Charles Mugler 1953, p. 77-78.)
- La très grande majorité des commentateurs (Albert Rivaud, Guy Donnay, Georges Kayas, Béatrice Bakhouche et Paul Couderc), après examen des différentes lectures proposées par les manuscrits du Timée en 40 b 9, et des problèmes soulevés par le témoignage d’Aristote (Du ciel, II, 13, 293 b 30), concluent à l’immobilité de la Terre chez Platon.
- Voir un résumé des diverses interprétations proposées depuis Aristote dans Charles Mugler, op. cit., Revue des Études Grecques, vol. 80, 1967, p. 211-212, et chez Léon Robin, p. 244 à 265. Albert Rivaud analyse en détail les difficultés de la notion de khôra p. 65 à 70. Emmanuel Falque (op. cit.) étudie les multiples implications philosophiques de cette notion chez Jacques Derrida.
- Selon Aristote, Platon identifie le lieu, τόπος, et l’emplacement, χώρα.
- Le mouvement, conditionné par des organes et des fonctions corporelles, est celui du vivant, mais aussi celui de la pensée qui se porte vers des objets purement intelligibles. Le rapport entre ces deux sortes de mouvement n’apparaît pas. Théophraste a critiqué cette psychogonie : c’est parce que le mouvement est lui-même mu que le principe du mouvement ne peut être que ce qui imprimera le mouvement.
- Dans Attente de Dieu (Fayard 1966, p. 113), Simone Weil, pénétrée de cette pensée de Platon, écrit : « Nous sommes comme des plantes qui auraient pour unique choix de s’exposer ou non à la lumière ». Elle a longuement interprété ce passage de Platon dans ses Intuitions pré-chrétiennes (Fayard, 1985, p. 31 sq.) Une position assez analogue a été exprimée Albert Gaudry et par Henri Bergson.
- Dans La République (Livre VII, 522 c-527 d), Platon cite les mathématiques, la géométrie et l’astronomie comme sciences éveilleuses du Bien.
- Spinoza développe la même idée dans son Éthique, V.
- La réincarnation d’une âme humaine sous une forme animale a soulevé des difficultés dès l’Antiquité. Dans le Phèdre (249 b), Platon affirme que l’âme d’une bête, qui n’a jamais contemplé la Vérité, ne peut pas subsister dans un corps humain.
- À l’inverse de Platon, Descartes, dans son traité sur La Dioptrique, conçoit correctement le rebondissement, sur une surface lisse, des particules de lumière comparables à des balles.
- Les mots « parties, et tripartition » de l’âme, utilisés par la plupart des traducteurs et commentateurs, sont étrangers à Platon, qui n’emploie que γένος et εἶδος, « espèce » pour définir des fonctions différentes. Le mot « partie », μέρος, μόριον, est réservé par Platon au corps. Dans le livre I (411 b) de son traité De l'Âme, Aristote met justement en cause la partition platonicienne de l’âme : « Qu’est-ce donc qui peut bien assurer la cohésion de l’âme, si la nature l’a rendue morcelable ? », écrit-il.
- Le Timée conserve le vocabulaire des récits eschatologique du Gorgias, du Phèdre (246 d-249 d) et du Phédon (81 e) qui représentaient déjà l’âme « enchaînée » au corps.
- Au sens étymologique, l’âme est donc qualifiée de « pédagogue », comme le note Jean-François Pradeau, op. cit., note 35 de la page 505.
- Pythagore et le mathématicien de haut niveau Archytas de Tarente se sont intéressés aux proportions numériques appliquées aux intervalles musicaux, et à la structure mathématique du cosmos. Le nom de Pythagore est associé à la découverte du fait que les consonances d’octave, de quarte et de quinte peuvent être exprimées par des rapports des nombres entiers, 1, 2, 3 et 4 : ces rapports, qui sont respectivement 1/2, 3/4 et 2/3, correspondent à la longueur de cordes vibrantes. Au XVIIe siècle, Leibniz et Newton contribuent à la découverte du calcul différentiel et intégral, et ces mathématiques classiques, qui utilisent des nombres réels, considèrent des grandeurs et des fonctions continues. Or, si la réalité du monde physique semble continue à l’échelle humaine — ce que traduit la formule de Leibniz selon laquelle « la nature ne fait pas de saut » —, à l’échelle nanométrique, cette réalité s’est révélée discontinue. Ainsi, les orbitales des électrons autour du noyau atomique manifestent des comportements discontinus ; ces orbitales sont caractérisées par des nombres quantiques, qui sont des nombres entiers ; elles ne peuvent donc pas être décrites par les lois mathématiques de Newton, et les nombres réels ne s’appliquent plus. C’est en ce sens que la mécanique quantique, découvrant des relations analogues entre, d’une part, les fréquences des ondes sonores et les nombres entiers, et d’autre part les orbitales des électrons dans l’atome, exprimées elles aussi par des nombres entiers, a renouvelé l’intérêt porté à Pythagore et aux théories pythagoriciennes du Timée de Platon.
- Pour Pierre Abélard, voir Bertrand Saint-Sernin, op. cit., p. 1821, note 1. Pour Hegel, mais aussi pour Ralph Cudworth et George Berkeley qui ont eu la même intuition, voir Jean-Louis Vieillard-Baron, op. cit., p. 384.
Références antiques
- Phédon, 80 a-b, traduction de Léon Robin, éditions Les Belles Lettres, 1967, p. 39.
- Platon, Timée [détail des éditions] [lire en ligne], 27 d, 28 a-b, 29 a, 30 c.
- Plutarque, De la musique, 44.
- Platon, La République, livre VII, 518 c, 534 a.
- Aristote, Physique, IV, 2, 209 b 12.
- Platon, Les Lois, X, 899 d et suiv. Dans ce dialogue, en IX, 871 a, pronoia est pris au sens juridique de « préméditation ».
- Aristote, De l'âme, I, 2, 404 b.
- Aristote, De l’âme, I, 2, 404 b.
- Aristote, De l'âme, I, 3, 406 b - 407 a.
- Aristote, Du ciel, II, 4, 331 b ; Météorologiques, I, 4, 341 b ; III, 7, 375 a et 376 a ; IV, 6, 383 a.
- Aristote, Du ciel, Livre II, chap. 13, 293 b.
- Platon, Lettre II, 312 d.
- Aristote, Physique, IV, 10, 218 a 33 sq.
- Aristote, Physique, IV, 2, 209 b.
- Platon, Phédon, 81 c et 83 d ; Timée, 44 b et 86 e.
- Platon, Gorgias, 523 a ; Phédon, 113 d ; La République, X, 615 sq.
- Platon, Protagoras, 345 d-e et 352 c ; Gorgias, 468 c sq., 480 b, 509 e ; Les Lois, V, 731 c et IX, 860 d.
- Platon, Phédon, 81 d sq. ; La République, 618 a sq.
- Platon, Théétète, 153 d-e et suiv.
- Platon, Le Sophiste, 266 b-c.
- Théophraste reprend cette définition : Des Sensations, 6 (Dox., 500, 14).
- Aristote, De l'Âme, II, 11, 422 b 31.
- Théophraste, Des sensations, 84.
- Théophraste, Des Sensations, Frag. I, Chap. XV.
- Corpus hippocratique, Περὶ παθῶν, c 19.
- Platon, Les Lois [détail des éditions] [lire en ligne], livre X, 892 a et 896 c.
- Platon, Philèbe, 47 e-50 c ; Les Lois, livre V, 730 e.
- Plutarque, De an. procr., 4, 1013 e.
- Aristote, Du ciel, I, 9, 279 a.
- Aristote, Du ciel, I, 10, 280 a.
- Aristote, De Mundo, 6, 397 b et 399 a ; Génération des animaux, I, 2, 716 a.
- « Fragments du Timée de Platon traduit par Cicéron »
- Philon d’Alexandrie, De specialibus legibus, I, 32, 50 ; Flavius Josèphe, Contre Apion II, 167-169.
- Maxime de Tyr, Dissertations, XI, 9.
- Platon, Timée, 41 d-e - 42 b.
Références bibliographiques
- Rivaud 1949, Notice, p. 5.
- Rivaud 1949, Notice, p. 6.
- Zeyl et Sattler 2019, p. 1, Overview of the Dialogue.
- Hadot 1983, p. 118.
- Rivaud 1949, Notice, p. 8.
- Robin 1942, p. 231.
- Rivaud 1949, Notice, p. 10-11.
- Robin 1942, p. 232.
- Robin 1942, p. 237.
- Robin 1942, p. 241.
- Rivaud 1949, p. 10.
- Robin 1942, p. 240.
- Rivaud 1949, p. 11.
- Desclos 2006, p. 180-184.
- Rivaud 1949, p. 15.
- Rivaud 1949, p. 16-17.
- Rivaud 1949, p. 18.
- (de) Heinz-Günther Nesselrath, Platon : Kritias, Göttingen, Vandenhoeck & Ruprecht, , p. 41-43.
- Bernard Mathieu, « Archytas de Tarente, pythagoricien et ami de Platon », Bulletin de l'Association Guillaume Budé, no 3, , p. 252 (lire en ligne).
- Leroux 2000, p. 9.
- Motte 1997, p. 9-10.
- Donnay 1960, p. 10.
- Saint-Sernin 2013, p. 1823.
- Mugler 1953, p. 57 et note 1.
- Vitrac 2006, p. 22 et 35.
- Saint-Sernin 2013, p. 1824.
- Galilée, L’Essayeur (Il Saggiatore), Paris, Les Belles Lettres, 1980, p. 141.
- Mugler 1948, Compte-rendu de Paul Couderc et Louis Séchan, p. 450.
- McHugh 2019, p. 168.
- Bernard Mathieu, « Archytas de Tarente, pythagoricien et ami de Platon », Bulletin de l'Association Guillaume Budé, no 3, , p. 243-244 (lire en ligne)
- Wilbur Knorr, « Mathématiques », dans Jacques Brunschwig et Geoffrey Lloyd, Le Savoir grec, Flammarion, , p. 422.
- Carlos Lévy, dans Le Savoir grec (de Jacques Brunschwig et Geoffrey Lloyd), Flammarion, 1996, p. 861.
- McHugh 2019, p. 173-174.
- Rivaud 1949, Notice, p. 24 et 82.
- Rivaud, Notice, p. 24 à 26.
- A. Vieira Pinto, « Note sur la traduction de Platon, Timée 43 b », Revue des Études Grecques, t. 65, nos 306-308, , p. 471-472 (lire en ligne).
- Rivaud, Notice, p. 27.
- Joseph Bidez et G. Leboucq, « Une anatomie antique du cœur humain : Philistion de Locres et le Timée de Platon », Revue des Études Grecques, t. 57, nos 269-273, , p. 15 à 18 (lire en ligne)
- Hadot 1983, p. 120.
- Rivaud 1949, Notice, p. 11.
- Brisson 1994.
- Saint-Sernin 2013, p. 1822.
- Daviault 2012, p. 77.
- Rivaud 1949, Notice, p. 11-12.
- Donald Ipperciel, « La vérité du mythe : une perspective herméneutique-épistémologique », p. 179.
- Daviault 2012, p. 78.
- Rivaud 1949, Notice, p. 13-14.
- Hadot 1983, p. 121.
- Hadot 1983, p. 130 et 131.
- Maurice Sachot, « Parménide d'Élée, fondateur de l'épistémologie et de la science, Commentaire analytique et synthétique du Poème », .
- Daviault 2012, p. 79.
- Zeyl et Sattler 2019, p. 5, Being and Becoming.
- Gauthier 1992, p. 150.
- Rivaud 1949, Notice, p. 13.
- Rivaud 1949, Notice, p. 68.
- Rivaud 1949, Notice, p. 66.
- Luc Brisson et F. Walter Meyerstein, Inventer l’Univers : Le problème de la connaissance et les modèles cosmologiques, Les Belles Lettres, (présentation en ligne)
- Brisson et Meyerstein, op. cit., p. 172.
- Brisson et Meyerstein, op. cit., p. 178.
- Brisson et Meyerstein, op. cit., p. 208-209.
- Gauthier 1992, p. 150-151.
- Gauthier 1992, p. 154.
- Leroux 2000, p. 8.
- Leroux 2000, p. 9 à 11.
- Morel 2002, p. 131.
- Leroux 2000, p. 13.
- Motte 1997, p. 6.
- Trouillard 1975, p. 292.
- Robin 1942, p. 238-239.
- Morel 2002, p. 144-147.
- Macé 2006, p. 103.
- Macé 2006, p. 104, note 33.
- Rivaud 1949, p. 64.
- Robin 1942, p. 237-238.
- Robin 1942, p. 239.
- Robin 1942, p. 242.
- Robin 1942, p. 236.
- Motte 1997, p. 10.
- Motte 1997, p. 11.
- Carl Huffman, « Pythagorisme », dans Jacques Brunschwig et Geoffrey Lloyd, Le Savoir grec, Flammarion, , p. 983.
- Robin 1942, p. 283.
- Rivaud 1949, Notice, p. 41 et 42.
- Rivaud 1949, Notice, p. 39.
- Rivaud 1949, Notice, p. 87-88.
- Pradeau 1998, p. 490-491.
- Kayas 1974, p. 294.
- Cornford 1997, p. 68.
- Rivaud 1949, Notice, p. 43.
- Kayas 1974, p. 312.
- Rivaud 1949, p. 53.
- Robin 1942, p. 236 et 285.
- Jean-François Mattéi, Platon, P.U.F., coll. « Que sais-je ? », 2005, p. 73-74.
- Rivaud 1949, p. 46 à 51.
- Robin 1942, p. 285.
- Vitrac 2006, p. 42 à 44.
- Robin 1942, p. 282.
- Bodéüs 1993, p. 257.
- Robin 1942, p. 284.
- Robin 1942, p. 289.
- Robin 1942, p. 286.
- Saint-Sernin 2012, p. 75.
- Zeyl et Sattler 2019, p. 8, Physics.
- Macé 2006, p. 100.
- Duhem 1913, p. 29-31.
- Rivaud 1949, p. 74 à 76.
- Macé 2006, p. 112.
- Rivaud 1949, p. 80.
- Saint-Sernin 2012, p. 77.
- Duhem 1913, p. 39.
- Robin 1942, p. 272.
- Besnier 2006, p. 135.
- Besnier 2006, p. 129.
- Robin 1942, p. 298-299.
- Besnier 2006, p. 130.
- Zeyl et Sattler 2019, p. 6, The receptacle.
- Robin 1942, p. 256.
- Rivaud 1949, p. 83.
- Rivaud 1949, p. 85-86.
- Rivaud 1949, Notice, p. 63.
- Mugler 1953, p. 56.
- Donnay 1960, p. 12.
- Kayas 1974, p. 310 et 318.
- Rivaud 1949, Notice, p. 56 à 59.
- McHugh 2019, p. 175.
- Rivaud 1949, Notice, p. 59-62.
- Mugler 1953, p. 83.
- Dorion 2006, p. 242 à 244.
- Mugler 1967, p. 50.
- Mugler 1967, p. 51.
- Rivaud 1949, p. 151, note 1.
- McHugh 2019, p. 176.
- Robin 1942, p. 255.
- Dixsaut 2003, p. 237-238.
- Thein 2002, p. 231.
- Dixsaut 2003, p. 238.
- Merker 2006, p. 79.
- Robin 1942, p. 252.
- Hernandez 2013, p. 1.
- Merker 2006, p. 88.
- Mugler 1967, p. 214.
- Rivaud 1949, p. 67.
- Rivaud 1949, p. 69.
- Pradeau 1995, p. 375.
- Mugler 1967, p. 213.
- (de) Eduard Zeller, Die Philosophie der Griechen, t. II, 1, 4e édition (lire en ligne), p. 740 sq..
- Robin 1942, p. 257 et 277.
- Martin Heidegger, Introduction à la métaphysique, 1983, coll. Tel, Gallimard, p. 75-76.
- Falque 2014, p. 156.
- Laurent 2006, p. 96.
- Rivaud 1949, p. 102.
- Rivaud 1949, p. 98 à 103.
- Rivaud 1949, p. 92.
- Pradeau 1998, p. 492-493 et 504-505.
- Rivaud 1949, p. 86.
- Rivaud 1949, p. 87.
- Pradeau 1998, p. 491.
- Gysembergh 2013, p. 620-621.
- Rivaud 1949, p. 91.
- Rivaud 1949, p. 89.
- Robin 1942, p. 326.
- Kucharski 1966, p. 5, 21-22, 29.
- Pradeau 1998, p. 509, note 43.
- Rivaud 1949, p. 88.
- Rivaud 1949, p. 116.
- Merker 2004, p. 16.
- Saudelli 2020, p. 3.
- Merker 2004, p. 18.
- Gysembergh 2013, p. 619-620.
- Saudelli 2020, p. 13 et 16.
- Charles Mugler, « Sur deux passages de Platon », Revue des Études Grecques, t. 69, nos 324-325, , p. 28-34 (lire en ligne)
- Rivaud 1949, p. 110.
- Rivaud 1949, p. 105.
- Rivaud 1949, p. 104.
- Merker 2006, p. 81.
- Merker 2006, p. 82.
- Rivaud 1949, p. 106.
- Merker 2006, p. 86, note 15.
- Merker 2006, p. 85.
- Merker 2006, p. 86.
- Merker 2006, p. 87.
- Rivaud 1949, p. 108.
- Rivaud 1949, p. 109.
- Rivaud 1949, p. 98.
- Pradeau 1998, p. 500-502.
- Rivaud 1949, p. 94-95.
- Pradeau 1998, p. 498.
- Pradeau 1998, p. 499.
- Rivaud 1949, p. 96.
- Pradeau 1998, p. 506.
- Pradeau 1998, p. 507-508.
- Pradeau 1998, p. 508-509.
- Rivaud 1949, p. 201, note 1.
- Pradeau 1998, p. 510.
- Pradeau 1998, p. 511-512.
- Rivaud 1949, p. 111.
- Rivaud 1949, p. 113.
- Rivaud 1949, p. 114.
- Rivaud 1949, p. 114-115.
- Zeyl et Sattler 2019, p. 9, Ethics.
- Georges Leroux, « La psychologie morale de Platon », Annuaire de l’École pratique des hautes études, Section des sciences religieuses, t. 109, , p. 327-330 (lire en ligne)
- Motte 1997, p. 5.
- Motte 1997, p. 7.
- Geneviève Normandeau, « Le sens des "timiôtera" et l'éthique du partage de la sophia chez Platon », Revue Philosophique de Louvain, t. 101, Quatrième série, no 3, , p. 367-382 (lire en ligne)
- Jean Irigoin, « Survie et renouveau de la littérature antique à Constantinople (IXe siècle) », Cahiers de civilisation médiévale, 5e année, no 19, , p. 287-302 (lire en ligne).
- « Archives et manuscrits, Grec 1807 », sur bnf.fr
- Rivaud 1949, Notice, p. 120.
- « Manuscript-Pal.gr.173 », sur digi.vatlib.it
- « Archives et Manuscrits, Grec 1812 », sur bnf.fr
- Gysembergh 2013, p. 620.
- Rivaud 1949, Notice, p. 3.
- Federico M. Petrucci, « Le témoignage du deuxième livre du Commentaire au Timée de Proclus sur la forme des arguments médio-platoniciens au sujet de la genèse du monde », Revue des Études Grecques, t. 127, no 2, , p. 338 (lire en ligne)
- Werner Jaeger (trad. Olivier Sedeyn), Aristote : Fondements pour une histoire de son évolution, L’Éclat, (ISBN 9782841-620142), p. 137-155 et 308-318.
- Bos 2009, p. 50.
- Baltes 1976, p. 5-6.
- Bos 2009, p. 52.
- Vitrac 2006, p. 12.
- Rivaud 1949, Notice, p. 4.
- Guy Rachet, « Saint-Augustin et les Libri Platonicorum », Bulletin de l'Association Guillaume Budé, no 3, , p. 341 (lire en ligne).
- Federico M. Petrucci, R.E.G. 2014, op. cit., p. 334.
- Ada Babette Neschke-Hentschke, « La transformation de la philosophie de Platon dans le Prologos d'Albinus », Revue Philosophique de Louvain, t. 89, Quatrième série, no 82, , p. 165 (lire en ligne)
- André-Jean Festugière et R. M. Tonneau, « Le Compendium Timaei de Galien », Revue des Études Grecques, t. 65, nos 304-305, , p. 97-98 (lire en ligne).
- Rivaud 1949, Notice, p. 42.
- Morlet 2008, p. 91.
- Morlet 2008, p. 99.
- Eugène de Faye, « De l'Originalité de la philosophie chrétienne de Clément d'Alexandrie », École pratique des hautes études, Section des sciences religieuses. Annuaire 1919-1920, , p. 15 (lire en ligne)
- Saint-Sernin 2013, p. 1821.
- Richard Dufour, « Tradition et innovations : le Timée dans la pensée plotinienne », Études platoniciennes, no 2, , p. 235-236 (lire en ligne)
- Federico M. Petrucci, R.E.G., 2014, op. cit., p. 339.
- Federico M. Petrucci, R.E.G., 2014, op. cit., p. 350-352.
- Luc Brisson, « Platonisme », dans Jacques Brunschwig et Geoffrey Lloyd, Le Savoir grec, Flammarion, , p. 977.
- Michel Huglo, La réception de Calcidius et des Commentarii de Macrobe à l’époque carolingienne, t. Scriptorium 44/I, , p. 5
- Bakhouche 2012, p. 347-349.
- Bakhouche 2012, p. 358.
- Gregory 1981, p. 676.
- Bakhouche 2012, p. 351-354.
- Michel Lemoine, « Guillaume de Conches, premier philosophe moderne ? », Bulletin de la Société Nationale des Antiquaires de France, no 1997, , p. 125 (lire en ligne).
- Étienne Gilson, « Le platonisme de Bernard de Chartres », Revue néoscolastique de philosophie, vol. XXVe année, no 97, , p. 10 (lire en ligne)
- Gilbert Boss, « Le combat d'Abélard », Cahiers de civilisation médiévale, vol. 31e année, no 121, , p. 17-27 (lire en ligne).
- Dante, Divine Comédie, Paradis (Divine Comédie), vers 22-24 et 49-63.
- Dante, La Divine Comédie, tome troisième, Paradis, Traduction André Pératé, édition Jean de Bonnot, 1972, p. 34.
- Counet, p. 5.
- Counet, p. 6.
- Counet, p. 14.
- Caroline Combronde, « Lectures du Timée à la Renaissance », Les Études classiques, no 71, , p. 107-121 (lire en ligne)
- Counet, p. 19.
- Saint-Sernin 2013, p. 1824.
- Duhem 1913, p. 40.
- Rivaud 1949, Notice, p. 28-29.
- Xavier Tilliette, Schelling : Une philosophie en devenir, t. 2, Paris, Vrin, , p. 487.
- Franck Fischbach, « Schelling : du Timée à la philosophie de la nature », dans F. W. J. Schelling (préf. Alexandra Michalewski), Le Timée de Platon, Presses Universitaires du Septentrion, , 141 p. (lire en ligne), p. 111-129.
- F. W. J. Schelling, Le Timée de Platon, op. cit., Préface d’Alexandra Michalewski.
- Franck Fischbach, op. cit.
- Vieillard-Baron 1976, p. 376.
- Vieillard-Baron 1976, p. 377.
- Vieillard-Baron 1976, p. 378.
- Vieillard-Baron 1976, p. 379.
- Friedrich Nietzsche, Introduction à l’étude des dialogues de Platon, p. 62, Éditions de l'Éclat, .
- Vieillard-Baron 1976, p. 384.
- Vieillard-Baron 1976, p. 389.
- Vieillard-Baron 1976, p. 391.
- Vieillard-Baron 1976, p. 392.
- Hernandez 2013, p. 5.
- Jacques Derrida, Khôra, Paris, Galilée, , p. 23 et 29-30.
- Jacques Derrida, Psyché, Paris, Galilée, , p. 502.
- (en) Alfred North Whitehead, Process and Reality, Part II, chap. II, New York, The Free Press, (lire en ligne), p. 71.
- A. N. Whitehead, op. cit., p. 93.
- Jean-Claude Dumoncel, « Lautman, Platon et Whitehead ».
- Jean-Michel Counet, « Whitehead et la philosophie ancienne » [PDF], sur academia.edu, p. 33.
- (de) Werner Heisenberg, « Gedanken der Antiken Naturphilosophie in der modernen Physik », Die Antike, vol. XIII, , p. 118-124.
- Werner Heisenberg, La nature dans la physique contemporaine, Paris, Gallimard N.R.F., , 191 p., p. 61-78.
- Werner Heisenberg, Physique et philosophie, Albin Michel, , 288 p. (ISBN 978-2226050502), p. 71 et 129.
- Petitot 1987, p. 80.
- Petitot 1987, p. 82.
- Catherine Chevalley, « Albert Lautman et le souci logique », Revue d'histoire des sciences, t. 40, Mathématique et philosophie : Jean Cavaillès et Albert Lautman, no 1, , p. 59 (lire en ligne).
- Catherine Chevalley, op. cit., p. 64.
- Albert Lautman, Nouvelles recherches sur la structure dialectique des mathématiques, Paris, Hermann, .
- Catherine Chevalley, op. cit., p. 61.
- Albert Lautman, Essai sur l’unité des sciences mathématiques dans leur développement actuel, Paris, Hermann, , p. 156.
- (en) Hermann Weyl, Symmetry, Princeton, Princeton University Press, , 160 p. (lire en ligne [PDF]), p. 6-8.
- Hermann Weyl, op. cit., p. 74.
- Hermann Weyl, op. cit., p. 77 à 79.
- Simone Weil, Réflexions à propos de la théorie des quanta (lire en ligne)
- Weil 1985, p. 25-26.
- Miklós Vető, La métaphysique religieuse de Simone Weil, Paris, L’Harmattan, , 206 p., p. 111.
- Miklós Vető, op. cit., p. 119-121.
- Weil 1985, p. 120-121.
- Miklós Vető, op. cit., p. 137, 152-153.
- Weil 1985, p. 30.
- Simone Weil, « Dieu dans Platon », La Source grecque, Gallimard, coll. Espoir, 1979, p. 129 à 131.
- (de) Carl Friedrich von Weizsäcker, Der Garten des Menschlichen : Beiträge zur geschichtlichen Anthropologie, Munich, Hanser, , p. 339, 343-345.
- Mohr et Sattler 2010, p. chap. 1, The Big questions.
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
Éditions en français
- Consulter la liste des éditions de cette œuvre
 .
. - Platon (trad. du grec ancien par Albert Rivaud), Timée, t. X, Paris, Les Belles Lettres, coll. « Collection des Universités de France », , 275 p., p. 3 à 123 : Notice.
 .Édition de référence
.Édition de référence - Luc Brisson (dir.), Timée : Platon, Œuvres complètes, Éditions Flammarion, (1re éd. 2006), 2204 p. (ISBN 9782081218109).

Études
- Sur l’ensemble du Timée et sa métaphysique
- Paul Kucharski, « Eschatologie et connaissance dans le Timée », Archives de Philosophie, vol. 29, no 1, , p. 5–36 (lire en ligne).

- Daniel Larose, « Le Démiurge du Timée de Platon ou la représentation mythique de la causalité paradigmatique de la forme du dieu », Methodos, no 16, (lire en ligne)
- Georges Leroux, « Origine, provenance et surgissement. La recherche de la cause originale dans le platonisme grec », Protée, vol. 28, no 1, , p. 7-18 (lire en ligne).

- Bertrand Saint-Sernin, « L’actualité du Timée », Comptes rendus des séances de l’Académie des Inscriptions et Belles-Lettres, vol. 157e année, no 4, , p. 1821-1831 (lire en ligne, consulté le ).

- Bertrand Saint-Sernin, « L’eau dans le Timée et les Lois », Publications de l’Académie des Inscriptions et Belles-Lettres, no 23, L’eau en Méditerranée de l’Antiquité au Moyen Âge. Actes du 22e colloque de la Villa Kérylos à Beaulieu-sur-Mer les 7 et 8 octobre 2011, , p. 75-83 (lire en ligne).

- Jean Trouillard, « Brisson, L., Le Même et l’Autre dans la structure ontologique du Timée de Platon. Un commentaire systématique du Timée de Platon, Paris, Klincksieck, 1974, 590 p. », Philosophiques, vol. 2, no 2, , p. 287-299 (présentation en ligne).
 .
. - (en) Donald Zeyl et Barbara Sattler, « Plato's Timaeus », dans Edward N. Zalta, The Stanford Encyclopedia of Philosophy, Metaphysics Research Lab. Stanford University, (lire en ligne).
 .
.
- Sur la cosmologie du Timée
- Béatrice Bakhouche, « Le difficile commentaire du Timée 38 d par Calcidius », Pallas. Revue d’études antiques, no 36, , p. 133-144 (lire en ligne, consulté le ).
 .
. - Bernard Besnier, « Genèses relatives et genèses originelles dans le Timée », Études platoniciennes, no 2, , p. 129-140 (lire en ligne, consulté le ).
 .
. - (en) Francis M. Cornford, Plato's Cosmology: The Timaeus of Plato, Translated with a Running Commentary, Indianapolis, Hackett Publishing Company, Inc., (1re éd. 1935) (ISBN 978-0-87220-386-0, lire en ligne).

- Guy Donnay, « Le système astronomique de Platon », Revue belge de philologie et d'histoire, t. 38, no 1, , p. 5-29 (lire en ligne, consulté le ).
 .
. - Pierre Duhem, Le Système du Monde : Histoire des doctrines cosmologiques de Platon à Copernic, t. I « La cosmologie hellénique », Paris, Librairie scientifique Hermann, , 530 p. (lire en ligne), p. 28-42, La cosmologie de Platon.
 .
. - Yvon Gauthier, « Luc Brisson et F. Walter Meyerstein : Inventer l'univers. Le problème de la connaissance et les modèles cosmologiques, éd. Les Belles Lettres, Paris, 1991 », Philosophiques, vol. 19, no 1, , p. 150-155 (lire en ligne).

- Georges J. Kayas, « L’âme de l’univers et la musique dans le Timée de Platon (34 b et ss.) », Bulletin de l’Association Guillaume Budé, no 3, , p. 287-329 (lire en ligne, consulté le ).

- Pierre Kerszberg, « Un univers excessivement mathématique : Platon et la cosmologie moderne », Études platoniciennes, no 9, , p. 63-81 (lire en ligne).

- Pierre-Marie Morel, « Le Timée, Démocrite et la nécessité », dans M. Dixsaut, A. Brancacci (éd.), Platon, source des présocratiques, Paris, Vrin, (lire en ligne), p. 129-150.

- Charles Mugler, « Le κένον de Platon et le πάντα ὁμοῦ d’Anaxagore », Revue des Études grecques, vol. 80, nos 379-383, , p. 210-219 (lire en ligne).

- Charles Mugler, « Les dimensions de l’univers platonicien d’après Timée 32 b », Revue des Études grecques, vol. 66, nos 309-310, , p. 56-88 (lire en ligne).

- Charles Mugler, « Démocrite et les postulats cosmologiques du Démiurge », Revue des Études anciennes, vol. 69, nos 1-2, , p. 50-58 (lire en ligne).

- Sur le Temps
- Monique Dixsaut, « Le temps qui s’avance et l’instant du changement (Timée 37 c-39 e ; Parménide 140 e-141 e ; 151 e-155 e) », Revue Philosophique de Louvain, vol. 101, no 2, , p. 236-264 (lire en ligne, consulté le ).

- (en) Mary R. McHugh, « Plato's Timaeus and Time », dans Heather L. Reid and Mark Ralkowski, Plato at Syracuse : Essays on Plato in Western Greece with a new translation of the Seventh Letter by Jonah Radding, Parnassos Press - Fonte Aretusa, , 167-184 p. (lire en ligne).

- Karel Thein, Le lien intraitable : Enquête sur le temps dans la République et le Timée de Platon, Paris, Librairie philosophique Vrin, , 350 p. (ISBN 978-2711615124).
 .
.
- Sur khora
- Jacques Derrida, Khôra, Paris, Éditions Galilée, coll. « Incises », (1re éd. 1993), 112 p. (ISBN 978-2-7186-0730-6).
- Emmanuel Falque, « Khora ou la “Grande bifurcation” : Dialogue avec Jacques Derrida », Archivio di Filosofia, vol. 82, nos 1-2, , p. 147-166 (lire en ligne).

- Marta Hernandez, « La khôra du Timée : Derrida, lecteur de Platon », Appareil, no 11, (lire en ligne, consulté le ).
 .
. - (en) David Keyt, « Aristotle on Plato’s Receptacle », American Journal of Philology, vol. 82, no 3, , p. 291-300 (lire en ligne, consulté le )
- Jérôme Laurent, « Note sur l'interprétation « matérialiste » de la χώρα par Luc Brisson », Études platoniciennes, no 2, , p. 93-96 (lire en ligne, consulté le ).
 .
. - Anne Merker, « Miroir et χώρα dans le Timée de Platon », Études platoniciennes, no 2, , p. 79-92 (lire en ligne, consulté le ).
 .
. - Jean-François Pradeau, « Être quelque part, occuper une place : Τόπος et Χώρα dans le Timée », Les Études philosophiques, no 3, , p. 375-399 (lire en ligne).

- (en) John Sallis, « The Χώρα », dans Chorology : On Beginning in Plato's Timaeus, Bloomington, Indiana University Press, (ISBN 978-0-253-046666, lire en ligne), p. 91-124 (Extraits en ligne)
- Sur les sciences
- Victor Gysembergh, « Une référence à la médecine de Cnide dans le débat philosophique entre Platon et Eudoxe », Revue des Études Grecques, t. 126, no 2, , p. 615-622 (lire en ligne).

- Arnaud Macé, « Activité démiurgique et corrélation des propriétés matérielles. Timée 55 e - 56 b », Études platoniciennes, no 2, , p. 97-128 (lire en ligne, consulté le ).
 .
. - Charles Mugler, Platon et la recherche mathématique de son époque, vol. XXVIII, Strasbourg-Zurich, P. H. Heitz, , 420 p. (présentation en ligne).
 .
. - Charles Mugler, La physique de Platon, t. XXV, Paris, Klincksieck, coll. « Études et commentaires », , 263 p. (présentation en ligne).
 .
. - Léon Robin, La pensée hellénique des origines à Épicure : Questions de méthode, de critique et d’histoire, Paris, P.U.F., , 555 p. (lire en ligne), Études sur la signification et la place de la physique dans la philosophie de Platon (p. 231-336).

- Bernard Vitrac, « Les mathématiques dans le Timée de Platon : le point de vue d’un historien des sciences », Études platoniciennes, no 2, , p. 11-78 (lire en ligne, consulté le ).
 .
.
- Sur l’anthropologie
- (it) Francesco Fronterotta, « Anima e corpo : immortalità, organicismo e psico-fisiologia nel Timeo platonico », Études platoniciennes, no 2, , p. 141-154 (lire en ligne)
- (it) Francisco L. Lisi, « El alma humana en el Timeo », Études platoniciennes, no 2, , p. 155-174 (lire en ligne)
- (en) Francisco L. Lisi, « Individual Soul, World Soul and the Form of the Good in Plato’s Republic and Timaeus », Études platoniciennes, no 4, , p. 105-118 (lire en ligne)
- Anne Merker, « Corps et châtiment chez Platon », Études platoniciennes, no 1, , p. 11-49 (lire en ligne).

- Jean-François Pradeau, « L’Âme et la moelle : Les conditions psychiques et physiologiques de l’anthropologie dans le Timée de Platon », Archives de Philosophie, vol. 61, no 3, , p. 489-518 (lire en ligne).

- Lucia Saudelli, « Les maladies de l’âme : Quelques problèmes dans le Timée de Platon », Mnemosyne, , p. 1-20 (lire en ligne).

- Sur la forme du Timée et le mythe platonicien
- Luc Brisson, Platon, les Mythes et les Mots, La Découverte, , 254 p. (ISBN 2-7071-1326-3).

- Marc-André Daviault, Fondements et usages philosophiques du mythe chez Platon, Canada, Université de Sherbrooke, , 134 p. (lire en ligne [PDF]), p. 75 à 97, Chap. III sur le Timée.
 .
. - Marie-Laurence Desclos, « Les prologues du Timée et du Critias : un cas de rhapsodie platonicienne », Études platoniciennes, vol. II, , p. 175-202 (lire en ligne).

- Pierre Hadot, « Physique et poésie dans le Timée de Platon », Revue de Théologie et de Philosophie, vol. 115, Troisième série, no 2, , p. 113-133 (lire en ligne).

- Jean-François Pradeau, Le Monde de la politique : Sur le récit atlante de Platon, Timée (17-27) et Critias, Sankt Augustin, Academia Verlag, , 367 p. (présentation en ligne)
- Pierre Vidal-Naquet, « Athènes et l’Atlantide. Structure et signification d’un mythe platonicien », Revue des Études Grecques, t. 77, nos 366-368, , p. 420-444 (lire en ligne, consulté le )
- Sur l’éthique et la théologie
- André Motte, « De la bonté du Démiurge (Platon, Timée, 29 d6-e4) », Revue de Philosophie Ancienne, vol. 15, no 1, , p. 3-13 (lire en ligne).

- Simone Weil, Intuitions pré-chrétiennes, Fayard, , 184 p. (ISBN 9782213-015606), p. 22-41.

- Sur la réception et la fortune du Timée
- Béatrice Bakhouche, « Lectures médiévales de l’harmonie musicale de l’âme selon Platon (Timée 35 b-36 b) : l’influence de Calcidius », Revue de musicologie, t. 98, no 2, , p. 339-362 (lire en ligne).
 .
. - (de) Matthias Baltes, Die Weltentstehung des platonischen Timaios nach den antiken Interpreten, 1976. (Philosophia antiqua, vol. XXX) (présentation en ligne, lire en ligne).

- Richard Bodéüs, « Du troisième genre au cinquième corps. Notes sur la critique du Timée de Platon dans le premier livre du traité De l’Âme d’Aristote », Revue philosophique de la France et de l'étranger, t. 183, no 2, , p. 239-262 (lire en ligne).

- Abraham Bos, « Aristote sur Dieu en tant qu'arché généséôs en opposition au Démiurge de Platon », Revue de Philosophie ancienne, vol. 27, no 1, , p. 39-57 (lire en ligne).

- Jean-Michel Counet, « La lecture du Timée par Nicolas de Cues », sur academia.edu, (non daté).

- Louis-André Dorion, « Platon, Proclus et l'autarcie du Monde (Timée 33 d) », Études platoniciennes, no 2, , p. 237-260 (lire en ligne).

- Tullio Gregory, « Le Platonisme au XIIe siècle », Revue des sciences philosophiques et théologiques, no 71, , p. 243-259 (présentation en ligne).

- (en) Richard D. Mohr et Barbara M. Sattler, One Book, the whole universe : Plato's Timaeus today, Parmenides Publishing, , 416 p. (ISBN 978-1-930972-32-2, présentation en ligne)
- Sébastien Morlet, « “Il est difficile de trouver celui qui est l’auteur et le père de cet univers…” : La réception de Tim. 28 c chez les Pères de l’Église », Études platoniciennes, no 5, , p. 91-100 (lire en ligne).

- (en) Jan Opsomer, « To find the maker and father. Proclus' exegesis of Plato Tim. 28 c 3-5 », Études platoniciennes, no 2, , p. 261-283 (lire en ligne).

- (fr + de + en + it) Ada Neschke-Hentschke (de) (dir.), Le Timée de Platon : Contributions à l’histoire de sa réception, Louvain, Paris, Peeters, , 348 p. (lire en ligne)
- Jean Petitot, « Refaire le Timée : Introduction à la philosophie mathématique d'Albert Lautman », Revue d'histoire des sciences, t. 40, Mathématique et philosophie : Jean Cavaillès et Albert Lautman, no 1, , p. 79-115 (lire en ligne).

- (it) Federico M. Petrucci, « L’esegesi e il Commento di Platone (A partire dall’esegesi della cosmogonia del Timeo) », Rivista di Storia della Filosofia, vol. 70, no 2, , p. 295-320 (lire en ligne).

- Jean-Louis Vieillard-Baron, « L’interprétation hégélienne du Timée, ou La philosophie de la nature », Revue de Métaphysique et de Morale, vol. 81e année, no 3, , p. 376-395 (lire en ligne).

Liens externes
- « Platon, Timée, traduction de Victor Cousin, 1822. » : seule édition ancienne référençant le Timée selon le système de référencement universel des œuvres de Platon.
- « Platon, Timée, traduction, notice et notes d’Émile Chambry, 1939 (Classiques Garnier) »
- Chalcidius (édition B.G. Teubner, Leipzig, 1876), « Platonis Timaeus et Commentarius »
- Ressources relatives à la recherche :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Portail de la philosophie antique
- Portail de la Grèce antique
