How to Find the Null Space of a Matrix

Last Updated: August 31, 2020

The null space of a matrix $A$ is the set of vectors that satisfy the homogeneous equation $A\mathbf {x} =0.$ Unlike the column space $\operatorname {Col} A,$ it is not immediately obvious what the relationship is between the columns of $A$ and $\operatorname {Nul} A.$

Every matrix has a trivial null space - the zero vector. This article will demonstrate how to find non-trivial null spaces.

Steps

1
Consider a matrix $A$ with dimensions of $m\times n$ .^{[1]
X
Research source} Below, your matrix is $3\times 5.$ $3\times 5.$
- $A={\begin{pmatrix}-3&6&-1&1&-7\\1&-2&2&3&-1\\2&-4&5&8&-4\end{pmatrix}}$
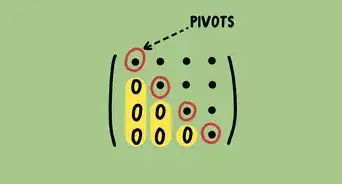
2
Row-reduce to reduced row-echelon form (RREF).^{[2]
X
Research source} For large matrices, you can usually use a calculator. Recognize that row-reduction here does not change the augment of the matrix because the augment is 0.
- ${\begin{pmatrix}1&-2&0&-1&3\\0&0&1&2&-2\\0&0&0&0&0\end{pmatrix}}$
- We can clearly see that the pivots - the leading coefficients - rest in columns 1 and 3. That means that $x_{1}$ and $x_{3}$ have their identifying equations. The result is that $x_{2},x_{4},x_{5}$ are all free variables.
Advertisement
3
Write out the RREF matrix in equation form.^{[3]
X
Research source}
- ${\begin{aligned}x_{1}-2x_{2}-x_{4}+3x_{5}&=0\\x_{3}+2x_{4}-2x_{5}&=0\end{aligned}}$
4
Reparameterize the free variables and solve.^{[4]
X
Research source}
- Let $x_{2}=r,x_{4}=s,x_{5}=t.$ Then $x_{1}=2r+s-3t$ and $x_{3}=-2s+2t.$
- $\mathbf {x} ={\begin{pmatrix}2r+s-3t\\r\\-2s+2t\\s\\t\end{pmatrix}}$
5
Rewrite the solution as a linear combination of vectors.^{[5]
X
Research source} The weights will be the free variables. Because they can be anything, you can write the solution as a span.
- $\operatorname {Nul} A=\operatorname {Span} \left\{{\begin{pmatrix}2\\1\\0\\0\\0\end{pmatrix}},{\begin{pmatrix}1\\0\\-2\\1\\0\end{pmatrix}},{\begin{pmatrix}-3\\0\\2\\0\\1\end{pmatrix}}\right\}$
- This null space is said to have dimension 3, for there are three basis vectors in this set, and is a subset of $\mathbb {R} ^{5},$ for the number of entries in each vector.
- Notice that the basis vectors do not have much in common with the rows of $A$ at first, but a quick check by taking the inner product of any of the rows of $A$ with any of the basis vectors of $\operatorname {Nul} A$ confirms that they are orthogonal.

Community Q&A

Question

How do you find the basis for the column space of a matrix?

Alphabet

Community Answer

Row reduce the matrix and pick the columns that have pivot points. Let us use the matrix A: 1 3 5, 5 6 7, 10 12 14. If we now reduce it, we get the following matrix: 1 0 -1, 0 1 2, 0 0 0. The first two columns have pivot positions, but the last column does not. So we go back to the original matrix A and the first two columns of the original matrix A form the basis of the column space.