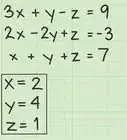How to Use Cramer's Rule

Co-authored by Hannah Madden

Last Updated: August 25, 2021

Solving linear equations can be a little tedious—but it doesn’t have to be! With Cramer’s rule, you can solve for 3 separate variables at the same time without solving the entire system of equations. After you find the matrices, you can use simple multiplication, addition, and subtraction to solve for x, y, and z.

Question 1 of 5:

What is Cramer’s rule used for?

It’s used for solving one of the variables in multiple equations. If you have a set of multiple linear equations (usually it’s a set of 3), you can use Cramer’s rule to solve for a variable without solving every single equation. Think of it as a shortcut to get the one system you need instead of spending time solving each equation.^{[1]
X
Research source}

Question 2 of 5:

How is Cramer’s rule calculated?

Cramer’s rule is defined as $x=Dx/D,y=Dy/D,z=Dz/D$ . This means that you can find the variables x, y, and z using Cramer’s rule. In every case, $D$ stands for “determinant,” and you can find it by using the x, y, and z values in your equation.^{[2]
X
Research source}

Question 3 of 5:

How do you find the determinants using Cramer’s rule?

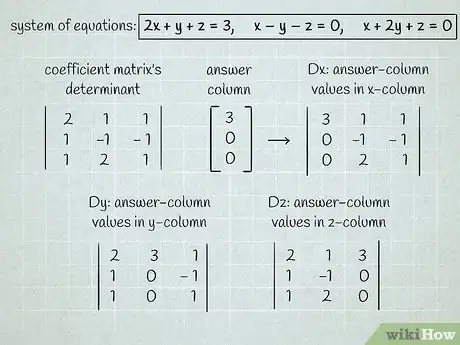
1
Find the determinants by categorizing the x, y, and z values. The determinants are the coefficients in your equations, or the numbers multiplied by the variable. For example, let’s use the equations: $2x+y+z=3,x-y-z=0,x+2y+z=0$ . To use Cramer’s rule, set up your determinants, or numbers, in a 3 x 3 matrix, or a small box. In the equations above, the box would look like this: $D=2,1,1,1,-1,1,1,2,1$ . The numbers are all of the values from each of the 3 equations.^{[3]
X
Research source}
2
Replace the x-column values with the answer column values. Now it’s time to determine what $Dx$ $Dx$ is. To do that, take your $D$ $D$ box and replace the x column (the one furthest on the left) with the answers from your original 3 equations. So, $Dx=3,1,1,0,-1,-1,0,2,1$ $Dx=3,1,1,0,-1,-1,0,2,1$ . This is your coefficient determinant, or the numbers you’ll use to solve for the x variable.^{[4]
X
Research source}
- Repeat this for y and z to find Dy and Dz. For instance, in the equations above, $Dy=2,3,1,1,0,-1,1,0,1$ and $Dz=2,1,3,1,-1,0,1,2,0$ .

Question 4 of 5:

How do you solve 3 equations using Cramer’s rule?

1
Expand the determinants by rewriting the first 2 columns. In order to use Cramer’s rule, you need to turn your 3 x 3 determinants into a 5 x 3 grid. For example, if you’re working with $D=2,1,1,1,-1,-1,1,2,1$ , add $2,1,1,$ and $1,-1,2$ on the end to create $D=2,1,1,2,1,1,-1,-1,1,-11,2,1,1,2$ .^{[5]
X
Research source}
2
Multiply along the downward and upward diagonals. In order to use Cramer’s rule, you have to simplify your 5 x 3 grid using multiplication. Take a look at your expanded box of determinants. Go through and multiply along the downward diagonals, and write the numbers below the box to keep track of them. Then, go through and multiply along the upward diagonals, writing your answers above the box.^{[6]
X
Research source}
- For instance, in the box above, the downward diagonals are: $(2)(-1)(1)=-2,(1)(-1)(1)=-1,(1)(1)(2)=2$ .
- The upward diagonals are: $(1)(-1)(1)=-1,(2)(-1)(2)=-4,(1)(1)(1)=1$ .
3
Add the downward diagonals and subtract the upward diagonals. Cramer’s rule states that we can use our multiplied numbers to find the variable that we need. In our example above, the equation would look like: $(-2)+(-1)+2-(-1)-(-4)-1=3$ . Therefore, $D=3$ .^{[7]
X
Research source}
4
Plug the numbers into the Cramer’s rule equation. Go through and do the steps above for $Dx,Dy,$ $Dx,Dy,$ and $Dz$ $Dz$ . Then, plug your answers into the equation $x=Dx/D,y=Dy/D,z=Dz/D$ $x=Dx/D,y=Dy/D,z=Dz/D$ to solve all three.^{[8]
X
Research source}
- Working with our example above, we can expand the Dx, Dy, and Dz variables in the same way. Once you multiply across the upward and downward diagonals, you’ll get: $Dx=(-3)+(0)+(0)-(0)-(-6)-(0)=3$ , $Dy=(0)+(-3)+(0)-(0)-(0)-(3)=-6$ , $Dz=(0)+(0)+(6)-(-3)-(0)-(0)=9$ .
- Plugging the answers into Cramer’s rule, our equation looks like this: $x=3/3,y=-6/3,z=9/3$ .
- Solve the equation to get: $x=1,y=-2,z=3$ .

Question 5 of 5:

What should you do if D = 0?

If D = 0, you can’t use Cramer’s rule. Unfortunately, D = 0 means that the equations don’t have a unique solution (the solution is infinite). Try using matrix row operations instead to solve your equations.^{[9]
X
Research source}
- If you’re just starting to learn Cramer’s rule, you won’t have to deal with D = 0 anytime soon.