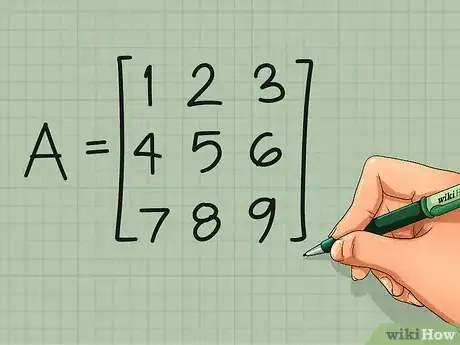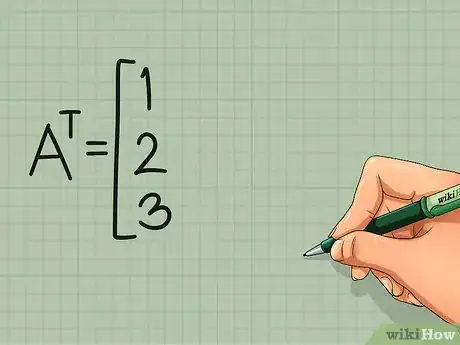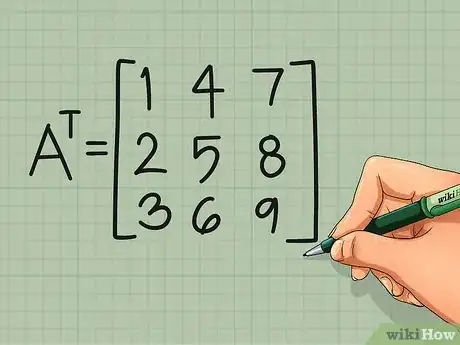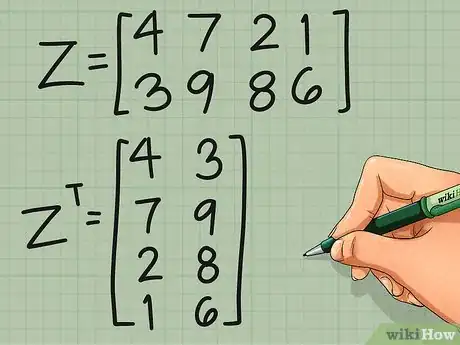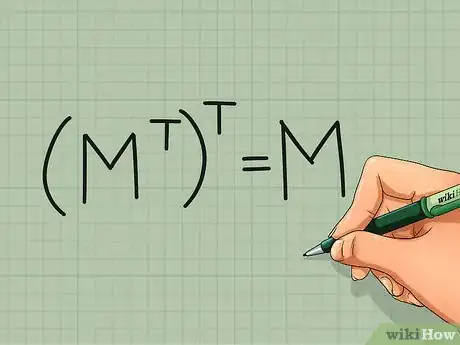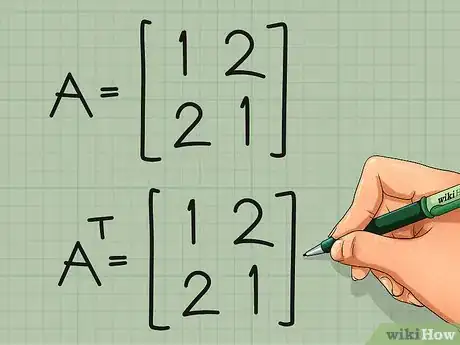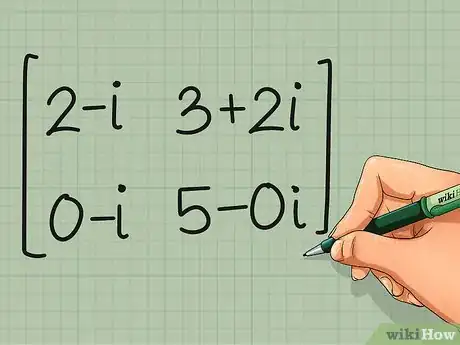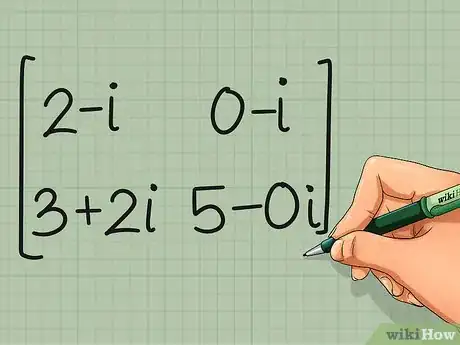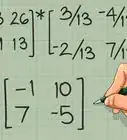How to Transpose a Matrix

Last Updated: October 12, 2022 References Approved

Matrix transposes are a neat tool for understanding the structure of matrices. Features you might already know about matrices, such as squareness and symmetry, affect the transposition results in obvious ways. Transposition also serves purposes when expressing vectors as matrices, or taking the products of vectors.^{[1]
X
Research source} If you're dealing with complex matrices, the closely related concept of a conjugate transpose will help you through many problems.

Part 1

Part 1 of 3:

Transposing a Matrix

1
Start with any matrix. You can transpose any matrix, regardless of how many rows and columns it has. Square matrices, with an equal number of rows and columns, are most commonly transposed, so we'll use a simple square matrix as an example:^{[2]
X
Research source}
- matrix A =
  1  2  3
  4  5  6
  7  8  9
2
Turn the first row of the matrix into the first column of its transpose. Rewrite row one of the matrix as a column:^{[3]
X
Research source}
- transpose of matrix A = A^T
- first column of A^T:
  1
  2
  3
Advertisement
3
Repeat for the remaining rows. The second row of the original matrix becomes the second column of its transpose. Repeat this pattern until you have turned every row into a column:^{[4]
X
Research source}
- A^T =
  1  4  7
  2  5  8
  3  6  9
4
Practice on a non-square matrix. The transposition is exactly the same for a non-square matrix. You rewrite the first row as the first column, the second row as the second column, and so forth. Here's an example with color-coding to show you where the elements end up:
- matrix Z =
  4 7 2 1
  3 9 8 6
- matrix Z^T =
  4  3
  7  9
  2  8
  1  6
5
Express the transposition mathematically. The concept is pretty simple, but it's good to be able to describe it in mathematics. No jargon is required beyond basic matrix notation:^{[5]
X
Research source}
- If matrix B is an m x n matrix (m rows and n columns), the transposed matrix B^T is an n x m matrix (n rows and m columns).^{[6]
  X
  Research source}
- For each element b_xy (xth row, yth column) in B, the matrix B^T has an equal element at b_yx (yth row, xth column).

Part 2

Part 2 of 3:

Special Cases

1
(M^{T^)T} = M. The transpose of a transpose is the original matrix.^{[7]
X
Research source} This is pretty intuitive, since all you're doing is switching the rows and columns. If you switch them again, you're back where you started.
2
Flip square matrices over the main diagonal. In a square matrix, transposition "flips" the matrix over the main diagonal. In other words, the elements in a diagonal line from element a₁₁ to the bottom right corner will remain the same. Each other elements will move across the diagonal and end up at the same distance from the diagonal, on the opposite side.
- If you can't visualize this, draw a 4x4 matrix on a piece of paper. Now fold is over the main diagonal. See how elements a₁₄ and a₄₁ touch? They trade places in the transpose, as does each other pair that touches when folded.
3
Transpose a symmetric matrix. A symmetric matrix is symmetric across the main diagonal. If we use the "flip" or "fold" description above, we can immediately see that nothing changes. All the element pairs that trade places were already identical.^{[8]
X
Research source} In fact, this is the standard way to define a symmetric matrix. If matrix A = A^T, then matrix A is symmetric.

Part 3

Part 3 of 3:

Conjugate Transpose of a Complex Matrix

1
Start with a complex matrix. Complex matrices have elements with a real and imaginary component. While you can take an ordinary transpose of these matrices, most practical calculations involve the conjugate transpose instead.^{[9]
X
Research source}
- Matrix C =
  2+i 3-2i
  0+i 5+0i
2
Take the complex conjugate. The complex conjugate changes the sign of the imaginary components, without altering the real components. Perform this operation for all elements of the matrix.^{[10]
X
Research source}
- complex conjugate of C =
  2-i 3+2i
  0-i 5-0i
3
Transpose the results. Take an ordinary transposition of the result. The matrix you end up with is the conjugate transpose of the original matrix.^{[11]
X
Research source}
- conjugate transpose of C = C^H =
  2-i 0-i
  3+2i 5-0i

Community Q&A

Question

How do I identity matrix transpose?

Robert Wilson

Community Answer

In matrix transpose all the rows of a matrix turn into columns and vice-versa. That's how you can identify a matrix transpose.
Question

Does a matrix transpose involve any calculation?

Community Answer

No, because to transpose is to rewrite the raw as a column ,starting with the first raw respectively.
Question

Given that B is a matrix, can B1 be the sign of its transpose?

Community Answer

Sure, that's a good way to remember how the two matrices are related. In general, mathematicians like to use B' or B^T to name the transpose to make it even easier to keep track.