Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 227 177 veces.
La fórmula más común para el área de un cuadrado es simple: es la longitud del lado al cuadrado o a2. Sin embargo, algunas veces solo conocerás la longitud de la diagonal del cuadrado que cruza entre los vértices opuestos. Si has estudiado los triángulos rectángulos, puedes encontrar una nueva fórmula de área que utiliza la diagonal como su única variable.
Pasos
Parte 1
Parte 1 de 2:Encontrar el área a partir de la diagonal
-
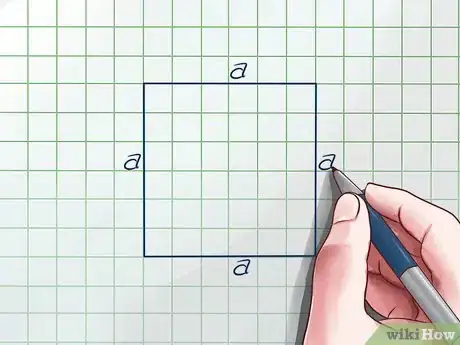
1Dibuja el cuadrado. Un cuadrado tiene cuatro lados iguales. Digamos que cada uno tiene una longitud de “a”.
-
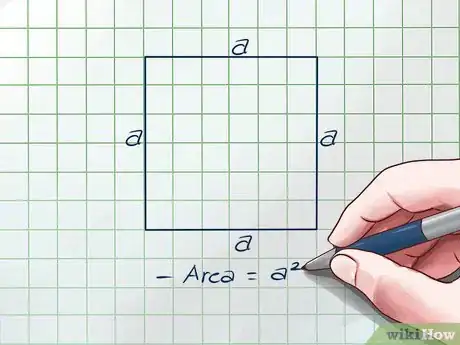
2Revisa la fórmula básica del área de un cuadrado. El área de un cuadrado es igual al largo por el ancho. Dado que cada lado es a, la fórmula sería Área = a x a = a2. Esta fórmula será útil más adelante.
-
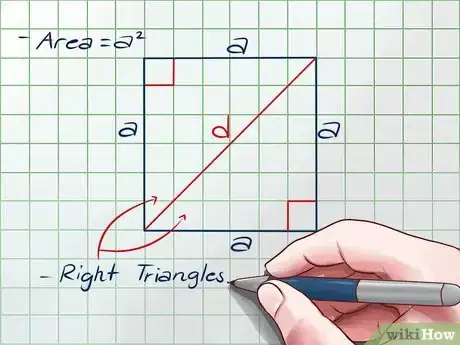
3Une dos esquinas opuestas a fin de hacer una diagonal. Indiquemos que la medida de esta diagonal es d unidades. Esta diagonal dividirá el cuadrado en dos triángulos rectángulos.
-
4Utiliza el teorema de Pitágoras en uno de los triángulos. El teorema de Pitágoras es una fórmula para encontrar la hipotenusa (el lado más largo) de un triángulo rectángulo: (lado uno)2 + (lado dos)2 = (hipotenusa)2 o . Ahora que el cuadrado está dividido por la mitad, puedes utilizar esta fórmula en uno de los triángulos rectángulos:
- Los dos lados más cortos del triángulo son los lados del cuadrado y cada uno tiene una longitud de a.
- La hipotenusa es la diagonal del cuadrado y tiene una longitud de d.
- Por lo tanto, tenemos que .
-
5Acomoda la ecuación de modo que las variables a2 estén en un lado. Recuerda que ya sabemos que el área del cuadrado es igual a a2. Si puedes juntar las variables a2 en un lado, tendrás una nueva ecuación para el área:
- Simplifica de modo que quede así: .
- Divide los lados entre 2 y quedará así: .
- Área =
- Área =
-
6Utiliza esta fórmula en el cuadrado del ejemplo. Estos pasos han demostrado que la fórmula Área = funciona para todos los cuadrados. Solo haz una diagonal que mida d y resuelve.
- Por ejemplo, digamos que un cuadrado tiene una diagonal que mide 10 cm.
- Área =
=
= 50 centímetros cuadrados.
Parte 2
Parte 2 de 2:Información adicional
-
1Encuentra la diagonal a partir de la longitud de un lado. El teorema de Pitágoras para un cuadrado con un lado a y una diagonal d te dará la fórmula . Obtén el valor de d si conoces la longitud del lado y quieres encontrar la de la diagonal:
-
- Por ejemplo, si un cuadrado tiene un lado de 18 cm, su diagonal será d = 18√2 o casi 25,46 cm.
- Si no tienes una calculadora, puedes utilizar 1,4 como una estimación de √2.
-
-
2Encuentra la longitud del lado a partir de la diagonal. Si te dan la diagonal y sabes que la diagonal de un cuadrado es , entonces podrás dividir ambos lados entre para obtener .
- Por ejemplo, un cuadrado con una diagonal de 10 cm tendrá lados de una longitud de cm.
- Si tienes que encontrar la longitud del lado y del área a partir de la diagonal, primero puedes utilizar esta fórmula y luego rápidamente cuadrar la respuesta para conseguir el área: Área centímetros cuadrados. Este proceso es menos preciso ya que es un número irracional que puede llevar a errores de redondeo.
-
3Interpreta la fórmula del área. Las matemáticas verifican la fórmula Área = ; sin embargo, ¿hay una manera de probarlo directamente? Bueno, es el área de un segundo cuadrado con la diagonal como lado. Dado que la fórmula completa es , puedes razonar que este segundo cuadrado tiene exactamente el doble del área del cuadrado original. Puedes probarlo tú mismo:
- Dibuja un cuadrado en un pedazo de papel. Asegúrate de que todos los lados sean iguales.
- Mide la diagonal. Dibuja un segundo cuadrado usando tal medida como su lado.
- Haz una copia de tu primer cuadrado de modo que tengas dos de ese tamaño. Separa los tres cuadrados.
- Corta los dos cuadrados más pequeños de cualquier forma de modo que puedas acomodarlos para que encajen dentro del cuadrado grande. Deben llenar el espacio de manera perfecta y eso te mostrará que el área del cuadrado más grande es exactamente el doble del área del cuadrado más pequeño.
Consejos
- Si no tienes una calculadora y necesitas una estimación más precisa para la raíz cuadrada de 2, hay formas de calcularla de forma manual. El método de Newton y Raphson es un ejemplo.[1]
- Esta ecuación simple se utiliza en muchos campos, incluyendo en cristalografía, química o arte. Por ejemplo, puedes utilizarla para calcular el área de un paisaje que puedes ver cuando haces una medición o también puedes emplearla cuando utilizas perspectiva en fotografía o pintura al medir la distancia que caminaste e imaginar una cuadrícula con esa distancia como diagonal.
- Si prefieres un enfoque más visual que el de las matemáticas o si quieres aprender la manera de utilizar cuadros y gráficos en arte, investiga sobre la trayectoria en espiral de una partícula o busca artículos sobre imágenes de Microsoft Excel, hojas de cálculos o gráficos.











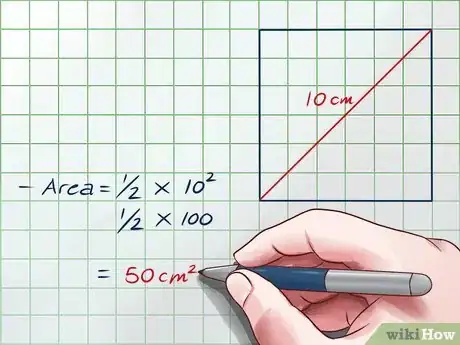

















-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)





wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 227 177 veces.