wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 9 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 15 818 veces.
En cálculo, cuando tienes una ecuación para y escrita en términos de x (como y = x2 -3x), es fácil utilizar técnicas de diferenciación básicas (lo que los matemáticos conocen como técnicas de “diferenciación explícita”) para hallar la derivada. Sin embargo, en el caso de las ecuaciones que son difíciles de reorganizar colocando y en un solo lado del signo igual (como por ejemplo x2 + y2 - 5x + 8y + 2xy2 = 19), se necesitará un método distinto. Con la ayuda de una técnica llamada diferenciación implícita, será fácil hallar las derivadas de ecuaciones con variables múltiples, ¡siempre y cuando ya conozcas los conceptos básicos de la diferenciación explícita!
Pasos
Método 1
Método 1 de 2:Diferenciar las ecuaciones simples con rapidez
-
1Diferencia los términos x como siempre. Al tratar de diferenciar una ecuación de variables múltiples como x2 + y2 - 5x + 8y + 2xy2 = 19, puede ser difícil saber por dónde empezar. Por suerte, el primer paso de la diferenciación implícita es el más sencillo. Para comenzar, simplemente diferencia los términos con x y las constantes en ambos lados de la ecuación según las reglas de diferenciación regulares (explícita). De momento, ignora los términos con y.
- Tratemos de diferenciar la ecuación simple anterior. La ecuación x2 + y2 - 5x + 8y + 2xy2 = 19 tiene dos términos con x: x2 y -5x. Si queremos diferenciar la ecuación, tendremos que resolverlos primero de la siguiente manera:
- x2 + y2 - 5x + 8y + 2xy2 = 19
- Baja el exponente “2” en x2 para colocarlo como coeficiente, elimina la x en -5x y cambia el 19 por 0)
- 2x + y2 - 5 + 8y + 2xy2 = 0
- Tratemos de diferenciar la ecuación simple anterior. La ecuación x2 + y2 - 5x + 8y + 2xy2 = 19 tiene dos términos con x: x2 y -5x. Si queremos diferenciar la ecuación, tendremos que resolverlos primero de la siguiente manera:
-
2Diferencia los términos con y y coloca "(dy/dx)" al lado de cada uno. En el siguiente paso, simplemente diferencia los términos con y de la misma manera en que lo hiciste con los términos de x. No obstante, esta vez agrega "(dy/dx)" al lado de cada uno de la misma manera en que agregarías un coeficiente. Por ejemplo, si diferencias y2, se convertirá en 2y(dy/dx). Por ahora, ignora los términos que tengan tanto x como y.
- En nuestro ejemplo actual, la ecuación se verá así: 2x + y2 - 5 + 8y + 2xy2 = 0. Realizaremos este paso de diferenciación de y de la siguiente manera:
- 2x + y2 - 5 + 8y + 2xy2 = 0
- Baja el exponente “2” en y2 para colocarlo como coeficiente, elimina la y en 8y y coloca un “dy/dx” al lado de cada uno.
- 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2xy2= 0
- En nuestro ejemplo actual, la ecuación se verá así: 2x + y2 - 5 + 8y + 2xy2 = 0. Realizaremos este paso de diferenciación de y de la siguiente manera:
-
3Utiliza la regla del producto o la regla del cociente para términos que tengan tanto x como y. Resolver términos que tengan x e y es un poco complicado, pero si conoces la regla del producto y la del cociente para la diferenciación, no tendrás problema. Si se multiplican los términos de x e y, utiliza la regla del producto ((f × g)' = f' × g + g × f'), reemplazando el término x por f y el término y por g.[1] Por otro lado, si los términos x e y se dividen entre sí, utiliza la regla del cociente ((f/g)' = (g × f' - g' × f)/g2), reemplazando el término en el numerador por f y el término en el denominador por g.[2]
- En nuestro ejemplo, 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2xy2 = 0, solo tenemos un término que tenga tanto x como y, que es 2xy2. Dado que x e y se multiplican entre sí, deberemos utilizar la regla del producto para diferenciarlos, de la siguiente manera:
- 2xy2 = (2x)(y2); coloca 2x = f e y2 = g en (f × g)' = f' × g + g × f'
- (f × g)' = (2x)' × (y2) + (2x) × (y2)'
- (f × g)' = (2) × (y2) + (2x) × (2y(dy/dx))
- (f × g)' = 2y2 + 4xy(dy/dx)
- Al agregarlo nuevamente a nuestra ecuación principal, obtendremos 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y2 + 4xy(dy/dx) = 0
- En nuestro ejemplo, 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2xy2 = 0, solo tenemos un término que tenga tanto x como y, que es 2xy2. Dado que x e y se multiplican entre sí, deberemos utilizar la regla del producto para diferenciarlos, de la siguiente manera:
-
4Aísla (dy/dx). ¡Ya casi terminas! Ahora todo lo que necesitas hacer es resolver la ecuación para (dy/dx). Parece difícil, pero generalmente no lo es; ten en cuenta que los dos términos a y b que se multiplican por (dy/dx) pueden escribirse como (a + b)(dy/dx) grcias a la propiedad distributiva de la multiplicación.[3] Esta táctica puede hacer que sea fácil aislar (dy/dx); solo coloca todos los demás términos en el lado opuesto de los paréntesis y luego divídelos entre los términos que están entre paréntesis al lado de (dy/dx).
- En nuestro ejemplo, podemos simplificar 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y2 + 4xy(dy/dx) = 0 de la siguiente manera:
- 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y2 + 4xy(dy/dx) = 0
- (2y + 8 + 4xy)(dy/dx) + 2x - 5 + 2y2 = 0
- (2y + 8 + 4xy)(dy/dx) = -2y2 - 2x + 5
- (dy/dx) = (-2y2 - 2x + 5)/(2y + 8 + 4xy)
- (dy/dx) = (-2y2 - 2x + 5)/(2(2xy + y + 4)
- En nuestro ejemplo, podemos simplificar 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y2 + 4xy(dy/dx) = 0 de la siguiente manera:
Método 2
Método 2 de 2:Utilizar técnicas avanzadas
-
1Conecta los valores (x, y) a fin de hallar (dy/dx) para cualquier punto. ¡Felicitaciones! Has diferenciado la ecuación de manera implícita, ¡lo cual no es una tarea fácil para los principiantes! Utilizar esta ecuación para hallar la pendiente (dy/dx) para cualquier punto (x, y) es tan simple como conectar los valores x e y para el punto en el lado derecho de la ecuación y luego resolver (dy/dx).
- Por ejemplo, supongamos que queremos hallar la pendiente en el punto (3, -4) para la ecuación anterior. Para hacerlo, deberemos sustituir 3 por x y -4 por y, resolviendo de la siguiente manera:
- (dy/dx) = (-2y2 - 2x + 5)/(2(2xy + y + 4)
- (dy/dx) = (-2(-4)2 - 2(3) + 5)/(2(2(3)(-4) + (-4) + 4)
- (dy/dx) = (-2(16) - 6 + 5)/(2(2(3)(-4))
- (dy/dx) = (-32) - 6 + 5)/(2(2(-12))
- (dy/dx) = (-33)/(2(2(-12))
- (dy/dx) = (-33)/(-48) = 3/48 o 0.6875.
- Por ejemplo, supongamos que queremos hallar la pendiente en el punto (3, -4) para la ecuación anterior. Para hacerlo, deberemos sustituir 3 por x y -4 por y, resolviendo de la siguiente manera:
-
2Utiliza la regla de la cadena para funciones dentro de otras funciones. Cuando se trata de problemas de cálculo (incluyendo los problemas de diferenciación implícita), es muy importante conocer la regla de la cadena. La regla de la cadena establece que para una función F(x) que puede escribirse como (f o g)(x), la derivada de F(x) es igual a f'(g(x))g'(x). Para problemas de diferenciación implícita que tengan una mayor dificultad, esto significa que es posible diferenciar diversas “partes” individuales de la ecuación y luego ensamblar el resultado.
- Como un ejemplo simple, supongamos que necesitamos hallar la derivada de sen(3x2 + x) como parte de un problema de diferenciación implícita más grande para la ecuación sen(3x2 + x) + y3 = 0. Si consideramos sen(3x2 + x) como "f(x)" y 3x2 + x como "g(x)", podremos hallar la diferenciación de la siguiente manera:
- f'(g(x))g'(x)
- (sen(3x2 + x))' × (3x2 + x)'
- cos(3x2 + x) × (6x + 1)
- (6x + 1)cos(3x2 + x)
- Como un ejemplo simple, supongamos que necesitamos hallar la derivada de sen(3x2 + x) como parte de un problema de diferenciación implícita más grande para la ecuación sen(3x2 + x) + y3 = 0. Si consideramos sen(3x2 + x) como "f(x)" y 3x2 + x como "g(x)", podremos hallar la diferenciación de la siguiente manera:
-
3Para ecuaciones con variables x, y, z, halla (dz/dx) y (dz/dy). Si bien no es común en el cálculo básico, algunas aplicaciones avanzadas pueden requerir realizar la diferenciación implícita de más de dos variables. Por cada variable adicional, necesitarás hallar una derivada extra con respecto a x. Por ejemplo, si trabajas con las variables x, y, z, necesitarás hallar (dz/dy) y (dz/dx). Podemos hacerlo al diferenciar la ecuación con respecto a x dos veces. La primera vez colocaremos un (dz/dx) cada vez que diferenciemos un término con z y la segunda colocaremos un (dz/dy) cada vez que diferenciemos una z. Luego, será cuestión de resolver (dz/dx) y (dz/dy).
- Por ejemplo, supongamos que queremos diferenciar x3z2 - 5xy5z = x2 + y3.
- En primer lugar, realicemos la diferenciación con respecto a x y coloquemos (dz/dx). ¡No olvides aplicar la regla del producto donde sea apropiado!
- x3z2 - 5xy5z = x2 + y3
- 3x2z2 + 2x3z(dz/dx) - 5y5z - 5xy5(dz/dx) = 2x
- 3x2z2 + (2x3z - 5xy5)(dz/dx) - 5y5z = 2x
- (2x3z - 5xy5)(dz/dx) = 2x - 3x2z2 + 5y5z
- (dz/dx) = (2x - 3x2z2 + 5y5z)/(2x3z - 5xy5)
- Ahora, hagamos lo mismo para (dz/dy)
- x3z2 - 5xy5z = x2 + y3
- 2x3z(dz/dy) - 25xy4z - 5xy5(dz/dy) = 3y2
- (2x3z - 5xy5)(dz/dy) = 3y2 + 25xy4z
- (dz/dy) = (3y2 + 25xy4z)/(2x3z - 5xy5)
Advertencias
- Siempre busca una parte en donde sea necesario aplicar la regla del cociente o del producto, pues es muy fácil de olvidar.




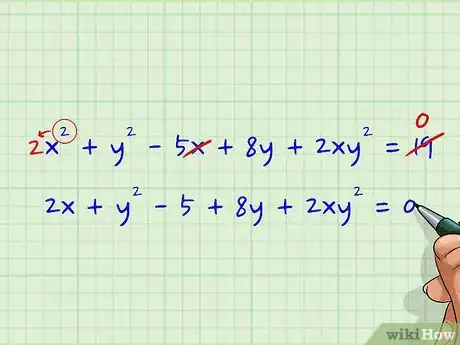



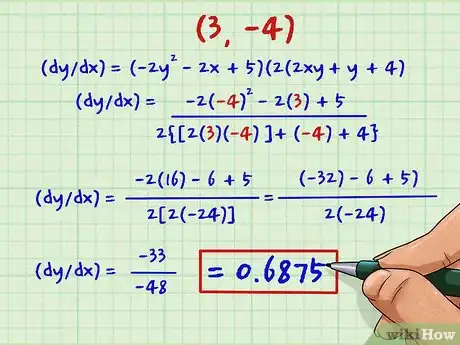
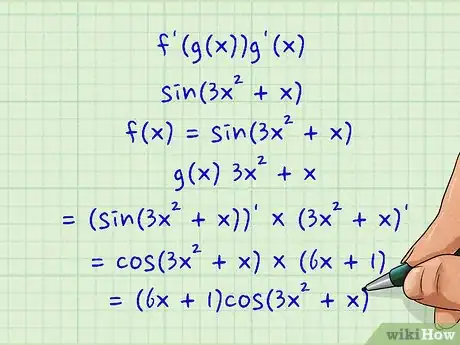








-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)




