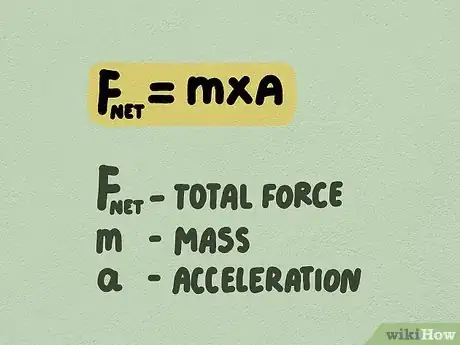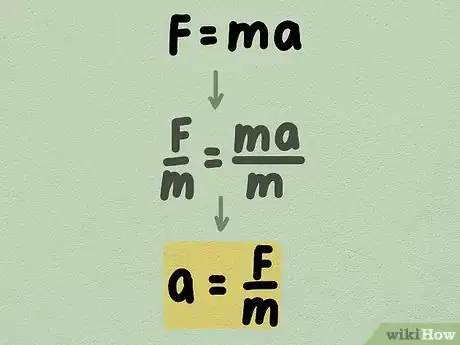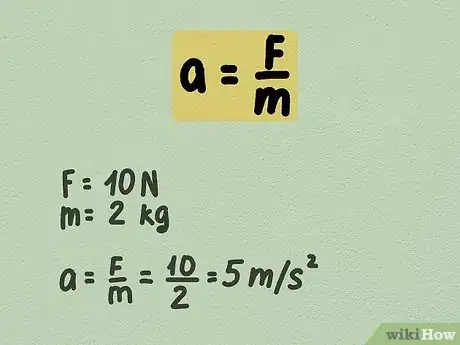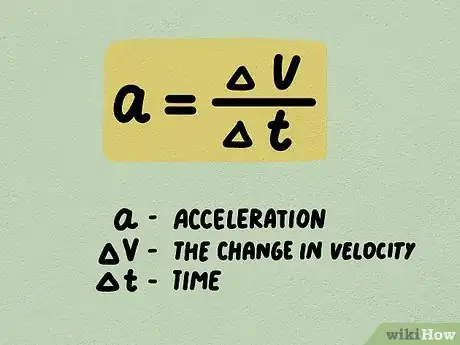Comment calculer l'accélération

L'accélération désigne le taux de variation de la vitesse d'un objet en mouvement ^{[1]
X
Source de recherche}. Si un objet maintient une vitesse constante, il n'y a pas d'accélération. L'accélération se produit lorsque la vitesse de l'objet varie. Si la variation de la vitesse est constante, cela signifie que l'accélération est nulle ^{[2]
X
Source de recherche}. Vous pouvez calculer le taux d'accélération, mesuré en mètres par seconde au carré, en fonction du temps qu'il faut pour passer d'une vitesse à une autre, ou en fonction de la force appliquée à l'objet.

Méthode 1

Méthode 1 sur 3:
Calculer l'accélération à partir d'une force

1
Définissez la deuxième loi de mouvement de Newton. Selon la deuxième loi de mouvement de Newton, lorsque les forces agissant sur un objet sont en déséquilibre, l'objet accélère. Cette accélération dépend des forces nettes qui agissent sur l'objet ainsi que de la masse de l'objet ^{[3]
X
Source de recherche}. En utilisant cette loi, l'accélération peut être calculée lorsqu'une force connue agit sur un objet dont vous connaissez la masse.
- La loi de Newton peut être représentée par la formule F_net = m x a, où F_net est la force totale agissant sur l'objet, m la masse de l'objet et a l'accélération de l'objet.
- Lorsque vous appliquez cette formule, utilisez le système d'unités métrique. Utilisez kilogrammes (kg) pour la masse, newtons (N) pour la force, et mètres par seconde au carré (m/s²) pour l'accélération.
2
Calculez la masse de l'objet. Pour trouver la masse d'un objet, pesez-le simplement sur une balance pour trouver sa masse en grammes. S'il s'agit d'un très grand objet, vous devez trouver une référence qui pourrait vous fournir la masse de l'objet. Les plus grands objets auront probablement leurs masses définies en kilogrammes (kg).
- Pour cette formule, vous devez convertir la masse en kilogrammes. Si la masse que vous avez déterminée est en grammes, convertissez-la en kilogrammes en la divisant par 1 000.
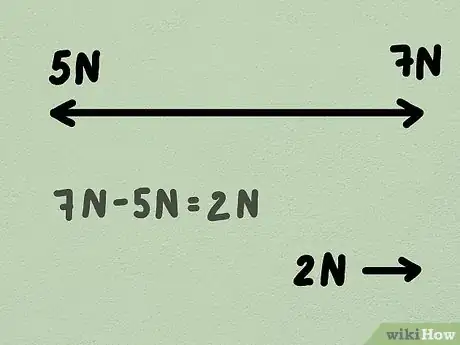
3
Calculez la force nette agissant sur l'objet. Une force nette est une force en situation de déséquilibre. Si vous avez deux forces opposant l'une à l'autre et que l'une est plus grande que l'autre, vous aurez une force nette dans la direction de la force la plus grande. L'accélération se produit lorsqu'une force déséquilibrée agit sur un objet, causant ainsi une variation de la vitesse dans la direction où la force le pousse ou le tire.
- Par exemple, disons que votre frère et vous jouez au tir à la corde. Vous tirez la corde sur la gauche avec une force de 5 newtons pendant que votre frère la tire vers la droite avec une force de 7 newtons. La force nette sur la corde est de 2 newtons vers la droite, dans la direction de votre frère.
- Pour bien comprendre les unités, sachez que 1 newton (N) est égal à 1 kilogramme-mètre/seconde au carré (kg-m/s² ^{[4]
  X
  Source de recherche}).
4
Réorganisez la formule F = ma pour calculer l'accélération. Vous pouvez réorganiser la formule pour calculer l'accélération en divisant les deux côtés par la masse, pour que a soit égal à F/m. Pour déterminer l'accélération, divisez simplement la force par la masse de l'objet en accélération.
- La force est directement proportionnelle à l'accélération, ce qui signifie qu'une force supérieure entrainera une plus grande accélération.
- La masse est indirectement proportionnelle à l'accélération, ce qui veut dire qu'une masse plus grande entrainera une décélération.
5
Utilisez la formule pour déterminer l'accélération. L'accélération est égale à la force nette agissant sur l'objet, divisée par la masse de l'objet. Une fois que vous avez défini les valeurs des variables, divisez simplement pour trouver l'accélération de l'objet.
- Par exemple, une force de 10 newtons agit uniformément sur une masse de 2 kilogrammes. Quelle est l'accélération de l'objet ?
- a = F/m = 10/2 = 5 m/s²
Publicité

Méthode 2

Méthode 2 sur 3:
Calculer l'accélération moyenne de deux vitesses

1
Élaborez l'équation de l'accélération moyenne. Vous pouvez calculer l'accélération moyenne d'un objet sur une période de temps en fonction de sa vélocité (la vitesse de son mouvement dans une direction spécifique), avant et après cette période de temps. Pour ce faire, vous devez connaitre la formule de l'accélération moyenne qui est : a = Δv / Δt où a désigne l'accélération, Δv la variation de la vitesse, et Δt le temps qu'il a fallu pour que cette variation se produise ^{[5]
X
Source de recherche}.
- La norme de l'accélération s'exprime en mètre par seconde au carré ou m/s².
- L'accélération est une grandeur vectorielle, ce qui signifie qu'elle a une magnitude et une direction ^{[6]
  X
  Source de recherche}. La magnitude est la quantité totale de l'accélération, tandis que la direction est la manière dont l'objet se déplace. Si elle ralentit, l'accélération sera négative.
2
Comprenez les variables. Vous pouvez aussi définir les formules de Δv et Δt : Δv = v_f - v_i et Δt = t_f - t_i où v_f est la vitesse finale, v_i la vitesse initiale, t_f le temps de fin, et t_i le temps de début ^{[7]
X
Source de recherche}.
- Puisque l'accélération a une direction, il est important de toujours soustraire la vitesse initiale de la vitesse finale. Si vous les inversez, la direction de votre accélération sera incorrecte.
- Sauf indication contraire dans le problème, le temps de début est généralement 0 seconde.
3
Utilisez la formule pour déterminer l'accélération. D'abord, écrivez la formule et toutes les variables que vous connaissez. La formule est a = Δv / Δt = (v_f - v_i)/(t_f - t_i). Soustrayez la vitesse initiale de la vitesse finale, puis divisez le résultat par l'intervalle de temps. Le résultat final représente l'accélération moyenne sur cette période de temps.
- Si la vitesse finale est inférieure à la vitesse initiale, l'accélération sera un nombre négatif ou la vitesse à laquelle l'objet ralentit.
- 1^er Exemple : une voiture de course accélère uniformément de 18,5 m/s à 46,1 m/s en 2,47 secondes. Quelle est l'accélération moyenne ?
  - Écrivez la formule : a = Δv / Δt = (v_f - v_i)/(t_f - t_i).
  - Définissez les variables : v_f = 46,1 m/s, v_i = 18,5 m/s, t_f = 2,47 s, t_i = 0 s.
  - Résolvez : a = (46,1 – 18,5)/2,47 = 11,17 m/s².
- 2^e Exemple : un motard roulant à 22,4 m/s s'arrête en 2,55 s après avoir freiné. Calculez sa décélération.
  - Écrivez la formule : a = Δv / Δt = (v_f - v_i)/(t_f - t_i).
  - Définissez les variables : v_f = 0 m/s, v_i = 22.,4 m/s, t_f = 2,55 s, t_i = 0 s.
  - Résolvez : a = (0 – 22,4)/2,55 = -8,78 m/s².
Publicité

Méthode 3

Méthode 3 sur 3:
Vérifier ses connaissances

1

La direction de l'accélération. Le concept physique de l'accélération ne correspond pas toujours à son application dans la vie réelle. Toute accélération a une direction, généralement représentée comme positive si elle est dirigée vers le haut ou la droite, et négative si elle est dirigée vers le bas ou la gauche. Vérifiez la validité de votre réponse en fonction de ce tableau.

L'allure d'une voiture	Variation de la vitesse	Direction de l'accélération
Le conducteur se déplace vers la droite (+) appuie sur la pédale de gaz	+ → ++ (plus positive)	positive
Le conducteur se déplace vers la droite (+) appuie sur les freins	++ → + (moins positive)	négative
Le conducteur se déplace vers la gauche (-) appuie sur la pédale de gaz	- → -- (plus négative)	négative
Le conducteur se déplace vers la gauche (-) appuie sur les freins	-- → - (moins négative)	positive
Le conducteur se déplace à une vitesse constante	ne varie pas	l'accélération est nulle

2
La direction de la force. On sait tous que la force entraine seulement l'accélération dans la direction de la force. Certains problèmes peuvent vous piéger avec des valeurs non pertinentes.
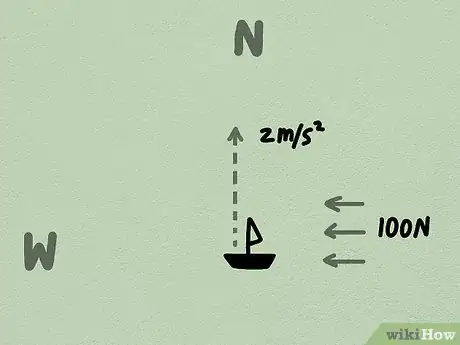
- Exemple de problème : un bateau jouet ayant une masse de 10 kg accélère vers le nord à 2 m/s². Un vent soufflant à l'ouest exerce une force de 100 newtons sur le bateau. Quelle est la nouvelle accélération vers le nord du bateau ?
- Solution: puisque la force est perpendiculaire à la direction du mouvement, il n'a pas d'effet sur le mouvement dans cette direction. L'accélération du bateau vers le nord est toujours de 2 m/s².
3
La force nette. Si plus d'une force agit sur un objet, combinez-les en une force nette avant de calculer l'accélération. Pour un problème en deux dimensions, cela ressemble au problème ci-dessous.
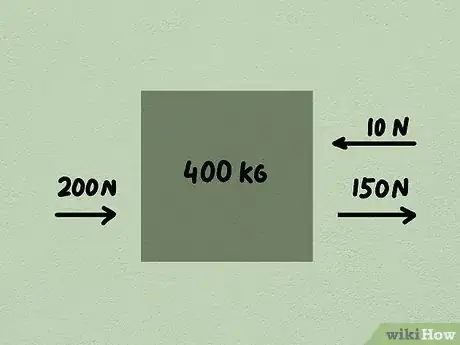
- Exemple de problème: April tire un récipient de 400 kg vers la droite avec une force de 150 newtons. Bob debout à gauche, quant à lui pousse le récipient avec une force de 200 newtons. Un vent soufflant vers la gauche exerce une force de 10 newtons. Quelle est l'accélération du récipient ?
- Solution: ce problème utilise un langage difficile pour essayer de vous piéger. Faites une représentation et vous verrez que les forces sont de 150 newtons vers la droite, 200 newtons vers la droite, et 10 newtons sur la gauche. Si la droite est la direction positive, la force nette est de 340 newtons (150 + 200 - 10). Accélération = F/m = 340 newtons / 400 kg = 0,85 m/s².
Publicité