Cet article a été coécrit par Chad Seegers, CRPC®. Chad Seegers est planificateur financier certifié (CFP®) et conseiller en planification de retraite certifié (CRPC®) pour Insight Wealth Strategies, LLC à Houston, Texas. Auparavant, Chad a collaboré avec Sagemark Consulting pendant plus de dix ans comme conseiller en patrimoine privé, et il est devenu un membre d’élite dans ce service. Chad réunit plus de 15 ans d'expérience, et il est spécialisé dans la planification de la retraite des employés et des cadres du secteur pétrolier et gazier ainsi que dans les stratégies de succession et d'investissement. Chad est aussi membre de soutien du World Affairs Council et leadeur émergent du Global Independence Center (GIC).
Il y a 7 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 44 164 fois.
L'intérêt composé diffère en cela de l'intérêt simple qu'il porte non sur le même capital de départ, mais chaque année, sur le capital augmenté des intérêts servis les années précédentes. Si avec un intérêt simple, le capital augmente de façon linéaire, avec l'intérêt composé, il croit de façon exponentielle. Chaque fois qu'avec un de vos placements, vous laissez le capital et les intérêts qu'il génère chaque année, vous bénéficiez d'un intérêt composé [1] . Si le calcul d'un intérêt est simple (vous retirez chaque année les intérêts produits), celui de l'intérêt composé est un un peu plus complexe.
Étapes
Partie 1
Partie 1 sur 3:Calculer un intérêt annuel composé
-
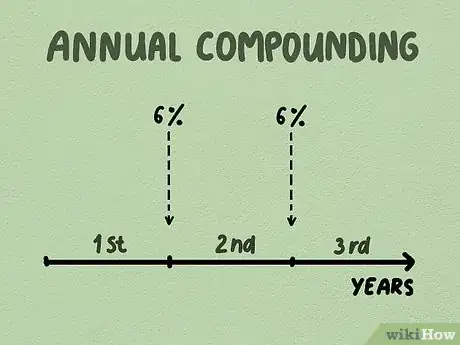
1Sachez ce qu'est un intérêt annuel composé. Le taux d'intérêt d'un placement (ou d'un emprunt) est souvent exprimé annuellement (6 % l'an). Si vous empruntez à 6 % par an, vous paierez chaque année, en sus du remboursement du prêt, 6 % d'intérêt, calculés sur le capital restant dû. L'intérêt simple est en fait un intérêt composé, mais sur une seule année [2] .
- Le taux d'intérêt est souvent annuel, mais il peut être mensuel, voire journalier.
- Il va de soi qu'un même taux vous rapportera plus mensuellement qu'annuellement.
- Un intérêt composé peut être analysé aussi bien du point de vue de l'investisseur que de celui de l'emprunteur. Plus la fréquence de capitalisation est élevée, plus l'investisseur s'enrichit et plus l'emprunteur paie d'intérêts. Tout dépend en fait du capital concerné.
- Ainsi, un compte d'épargne classique rapporte des intérêts une fois l'an, ce qui laisse peu de place à un enrichissement rapide. Par contre, si vous prêtez au mois ou à la semaine, vous vous enrichirez.
-
2Calculez l'intérêt composé sur la première année. Prenons l'hypothèse que vous déteniez des valeurs du Trésor pour un montant de 1 000 € à 6 % de taux d'intérêt l'an. Bien qu'ayant des taux de rémunération moindres, les assurances-vie sont de ce type-là [3] .
- Les intérêts servis la première année se monteront donc à 60 € (1 000 € x 6 % = 60 €).
- Pour calculer les intérêts générés la deuxième année, vous devez partir du capital auquel vous aurez ajouté les intérêts de la première année. Dans notre exemple, le capital de la deuxième année est celui de départ (1 000 €), augmenté des intérêts de la première année (60 €), ce qui fait 1 060 €. C'est sur ce nouveau capital que seront calculés les intérêts de la deuxième année.
-
3Calculez vos gains sur plusieurs années. Avant de placer votre argent à un taux composé, faites une projection sur plusieurs années. Vous comprenez bien que plus le temps s'écoule, plus votre capital augmente [4] .
- Pour la deuxième année, multipliez le nouveau capital par le taux d'intérêt. Dans notre exemple, cela donne : 1 060 € X 6 % = 63,60 €. Vous avez gagné 3,60 $ de plus que lors de la première année : c'est normal, puisque vous aviez un capital plus important (1 060 € au lieu de 1 000 €).
- Pour la troisième année, votre capital de départ sera de 1 123,60 (1 060 € + 63,60 €) et 6 % de ce capital équivalent à 67,42 €. Si vous maintenez votre placement, cet argent va venir grossir le capital.
- Vous comprenez dès lors que plus le temps passe, plus l'intérêt augmente. C'est intéressant si vous êtes l'investisseur, cela l'est moins si vous êtes l'emprunteur : tout est question de point de vue !
- Si vous placez ce capital en intérêt simple ou si vous retirez chaque année les intérêts sans cependant toucher au capital, votre pécule vous rapportera chaque année la même somme : 60 €.
-
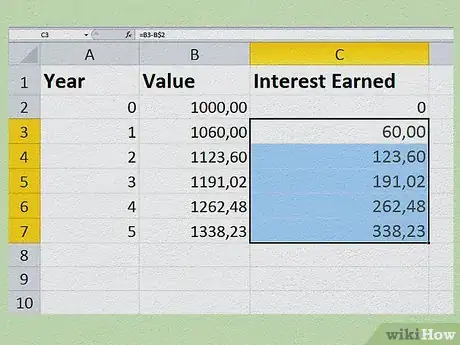
4Créez un document Excel pour vos projections. Ce genre de document est très pratique, car il permet, une fois toutes les cellules paramétrées, de faire des simulations avec des résultats immédiats. Ouvrez un classeur vierge et nommez les colonnes A, B et C, respectivement Année, Capital et Intérêt
- Entrez vos années (5 ans, par exemple) dans les cellules A2 à A7.
- Entrez votre capital de départ dans la cellule B2. Si vous comptez investir
1 000 €, tapez 1 000 (sans unité). - Dans la cellule B3, tapez =B2*1,06, puis validez avec la touche Entrée. Le 1,06 signifie que le taux d'intérêt est fixé à 6 % (0,06). Cliquez sur la poignée de recopie de B3 (en bas et à droite), puis faites glisser le curseur jusqu'à la cellule B7 : toutes les cellules contiennent alors la formule de B3.
- Placez un 0 dans la cellule C2. Dans la cellule C3, tapez =B3-B$2, puis validez avec la touche Entrée. Dans cette cellule, vous verrez apparaitre la différence entre B3 et B2, différence qui est en fait l'intérêt servi. Comme précédemment, cliquez sur la poignée de recopie de C3, puis faites glisser le curseur jusqu'à la cellule C7 : toutes les cellules contiennent alors la formule de C3.
- Si vous voulez une prévision sur un plus grand nombre d'années, copiez les formules sur le nombre d'années voulues. Vous pourrez aussi changer facilement les paramètres pour voir ce que cela donne.
Publicité
Partie 2
Partie 2 sur 3:Calculer l'intérêt composé sur un placement
-
1Retenez la formule de l'intérêt composé. Elle permet de calculer le capital disponible au bout d'un certain nombre d'années (): c'est ce qu'on appelle aussi la valeur finale. La formule se présente comme suit : . Les données sont les suivantes :
- est le capital disponible au bout d'une période (valeur finale),
- est le capital de départ (valeur initiale),
- représente le taux d'intérêt périodique,
- représente la fréquence de capitalisation (le nombre de versements d'intérêts dans l'année),
- représente le nombre de périodes (années).
-
2Récupérez toutes les données. Pour pouvoir utiliser la formule, vous devez être en possession de toutes les données. Cette formule est très utile quand la fréquence de capitalisation est supérieure à 1, c'est-à-dire quand le taux est hebdomadaire, mensuel, semestriel… La difficulté de cette formule est qu'il ne faut pas se tromper dans les périodes, la formulation du taux, l'application numérique… et les calculs [5] .
- Déterminez le capital de départ. Si vous faites des projections de placement, dites-vous bien que ce capital investi détermine le capital final. Si vous faites plusieurs calculs avec des capitaux différents, ne mélangez pas vos résultats, sans quoi votre analyse serait fausse. Imaginons que vous vouliez placer 5 000 €.
- Repérez le taux d'intérêt. S'il est facile d'identifier la valeur du taux, il faut surtout identifier sa nature, à savoir s'il est annuel, mensuel… Dans notre exemple, nous poserons que les 5 000 € sont placés à un taux d'intérêt annuel de 3,45 %.
- Le taux d'intérêt doit être transformé en une valeur décimale et pour cela, il suffit de le diviser par 100. Ici, divisons 3,45 % par 100, ce qui donne 0,0345.
- Pour déterminer la fréquence de capitalisation, vous devez savoir si l'intérêt est versé annuellement, mensuellement ou quotidiennement. À titre d'exemple, dans le cas d'une composition mensuelle, la fréquence de capitalisation () est de 12.
- Fixez-vous une durée de placement. Si votre placement n'a pas de limite dans le temps, vous pouvez faire une projection à 5 ou 10 ans. Si le placement est limité, ce qui est le cas des obligations ou des plans d'épargne, vous pouvez calculer votre capital à la maturité du placement. Nous prendrons comme exemple une maturité de 2 ans, nous entrerons donc la valeur 2.
-
3Utilisez correctement la formule. Faites l'application numérique sans vous tromper durant le remplacement des valeurs littérales. Deux erreurs sont fréquentes : ne pas mettre le taux d'intérêt sous forme décimale et se tromper pour , la fréquence de capitalisation.
- Avec les valeurs de notre exemple, la formule est la suivante :
. - Lorsque vous avez une formule avec des opérations imbriquées les unes dans les autres, sachez qu'il existe un ordre des opérations, certaines sont prioritaires, comme celles à l'intérieur de parenthèses.
- Avec les valeurs de notre exemple, la formule est la suivante :
-
4Faites les calculs. Simplifiez progressivement la formule pour obtenir le résultat voulu, les opérations à l'intérieur de parenthèses étant prioritaires [6] .
- Calculez d'abord la fraction à l'intérieur des parenthèses, ce qui donne :
. - Faites la somme indiquée dans les parenthèses, ce qui donne :
. - Calculez l'exposant. Il s'agit d'un produit qu'il convient à présent de calculer, la formule devient la suivante : .
- Calculez la valeur élevée à la puissance. Sur une calculatrice, entrez la base (ici, 1,00288), appuyez sur la touche x^y, puis entrez la puissance (ici, 24). Pour terminer, validez avec la touche Entrée. Tous calculs faits, la formule se présente alors sous cette forme : .
- Pour finir, multipliez votre capital par le nombre entre parenthèses. Le résultat obtenu, à savoir 5 357,50 (5 000 x 1,0715), est votre capital après deux ans de placement.
- Calculez d'abord la fraction à l'intérieur des parenthèses, ce qui donne :
-
5Soustrayez votre capital de départ de cette dernière somme. Cela vous donnera le montant des intérêts gagnés sur la période considérée.
- Dans le cas étudié, soustrayez votre capital de départ (5 000 €) de la valeur finale trouvée, soit 5 357,50 €, ce qui donne :
5 375,50 € - 5 000 € = 357,50 €. - Sur deux ans, vous gagnez au titre des intérêts 357,50 €.
Publicité - Dans le cas étudié, soustrayez votre capital de départ (5 000 €) de la valeur finale trouvée, soit 5 357,50 €, ce qui donne :
Partie 3
Partie 3 sur 3:Calculer un placement à versements périodiques capitalisés
-
1Retenez la formule de calcul. C'est facile à comprendre : si vous placez votre argent à un intérêt composé tout en faisant des versements réguliers, votre capital augmentera plus vite que si vous vous contentez des seuls intérêts. La formule de calcul est alors un peu plus longue que la précédente, mais le principe demeure le même. La formule se présente comme suit :
[7] . Vous reconnaissez les variables précédentes, une nouvelle () fait son apparition :- est le capital de départ et , le capital disponible au bout d'une période ,
- représente le taux d'intérêt périodique,
- représente la fréquence de capitalisation (le nombre de versements d'intérêts dans l'année),
- est le nombre de périodes,
- représente le montant du versement périodique.
-
2Récupérez toutes vos variables. Pour calculer un placement à versements périodiques capitalisés, vous devez avoir le montant du capital de départ (valeur initiale), le taux d'intérêt annuel, la fréquence de capitalisation, la durée en années envisagée et le montant du versement mensuel. Toutes ces informations seront inscrites dans le contrat passé, par exemple, avec un établissement financier.
- Pour pouvoir être utilisé dans la formule, le taux d'intérêt doit être transformé en une valeur décimale et pour cela, il suffit de le diviser par 100. Ici, divisons 3,45 % par 100, ce qui donne 0,0345.
- La fréquence de capitalisation est le nombre de versements, dans l'année, de l'intérêt. Si le taux est annuel, il y aura un seul versement, s'il est mensuel, 12 et journalier, 365 (ou 366).
-
3Faites une projection chiffrée. Pour compléter la simulation, imaginons que vous versiez 100 € par mois sur ce placement. Vous investissez donc au départ un capital de 5 000 €, l'intérêt est servi chaque mois et le taux d'intérêt annuel est de 3,45 %. Nous prendrons une durée de placement de deux ans.
- Muni de toutes ces informations, la formule littérale transformée devient :
.
- Muni de toutes ces informations, la formule littérale transformée devient :
-
4Faites les calculs. Comme précédemment, l'ordre des opérations doit être respecté, ce qui signifie ici calculer ce qui est entre parenthèses.
- Calculez en premier les fractions entre parenthèses. L'opération est à faire une seule fois, mais trois quantités doivent être remplacées par le résultat obtenu, soit 0,00288. La formule se présente alors ainsi :
. - Faites les deux sommes entre parenthèses. Il s'agit de la même opération qui consiste à ajouter 1 à 0,00288. La formule devient plus simple :
. - Calculez les exposants. Ils sont pour l’instant sous forme de multiplication, il faut les calculer, c’est simple, pour pouvoir élever plus tard à ces puissances. Ici, il faut multiplier 2 par 12, ce qui donne une puissance de 24. La formule devient :
. - Calculez les valeurs ayant un exposant. La valeur sera multipliée par elle-même autant de fois que l’indique l’exposant. Sur une calculatrice, entrez la base (valeur qui va être élevée à la puissance, ici 1,00288), tapez ensuite sur la touche et enfin, entrez la puissance (ici, ce sera 24), ce qui donne : .
- Faites la seule soustraction de la formule, à savoir retirer 1 de 1,0715, soit 0,0715. La formule est de plus en plus simple :
. - Calculez le numérateur de la fraction en multipliant le montant de la mensualité (100) par la valeur trouvée précédemment (0,0715). La formule se présente comme suit : .
- Calculez la fraction. Vous obtenez : .
- Faites la somme. Comme vous le voyez, la formule n’est plus qu’une simple addition qui vous donnera la valeur finale au bout de deux ans. Additionnez 5 357,50 € et 2 482,64 €, soit 7 840,14 €.
- Calculez en premier les fractions entre parenthèses. L'opération est à faire une seule fois, mais trois quantités doivent être remplacées par le résultat obtenu, soit 0,00288. La formule se présente alors ainsi :
-
5Calculez les intérêts gagnés. Pour le savoir, vous devez soustraire de la valeur finale et le capital de départ et les versements faits durant ces deux années, soit 24 mensualités. Dans notre cas, de 7 840, 14 € vous devez soustraire le capital de départ (5 000 €) et les 24 mensualités de 100 € (2 400 €), ce qui fait un total de 7 400 €. Vos intérêts se montent donc sur deux ans à 440,14 €, résultat de l'opération 7 840,14 - 7 400.
-
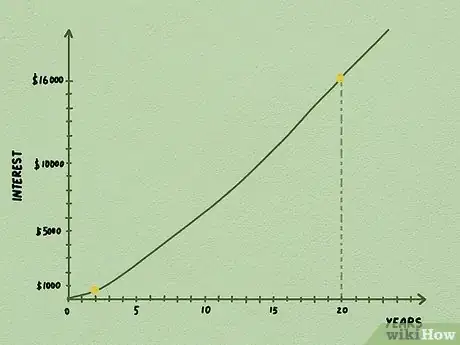
6Essayez-vous à d'autres projections. Nous avons ici fait une prévision à deux ans, mais rien ne vous empêche d'en faire une à 20 ans. En gardant les mêmes données de base, mais en changeant l'exposant (240 au lieu de 24), la valeur finale de votre placement s’élèvera à environ 45 000 €, de laquelle vous retirerez les 5 000 € de départ et les 24 000 € versés, ce qui fait que vous aurez gagné environ 16 000 € (45 000 € - 29 000 €).Publicité
Conseils
- Pour vous faciliter les calculs, sachez qu'il existe des calculatrices d'intérêt composé sur Internet. Nous vous conseillons celle-ci, mais il en existe d'autres. Il suffit alors d'entrer les différents paramètres et de valider vos choix.
- Avec l’intérêt composé, il existe une astuce qui permet de savoir rapidement en combien de temps un capital sera doublé : c’est la règle dite « des 72». Pour cela, divisez 72 par le taux d’intérêt, par exemple 4 %, ce qui fait 18 (= 72/4). Ce résultat est le nombre d’années au terme desquelles votre capital aura doublé… à peu de choses près. C’est bien entendu un ordre d’idées, non une réponse précise [8] .
- Avec telle ou telle formule, vous allez pouvoir faire des prévisions en modifiant à votre guise le capital de départ, le taux d'intérêt, la fréquence de capitalisation et la durée du placement. Au bout du compte, vous choisirez, en fonction de votre situation, l'investissement le plus rentable.
Références
- ↑ https://www.lucbrialy.com/interets-composes.html
- ↑ http://gerard.ledu.free.fr/PDF/FI_INT1.pdf
- ↑ https://financer.com/fr/finances/calculatrice/calcul-interets-composes/
- ↑ http://www.moneychimp.com/international/fr/calculator/compound_interest_calculator.htm
- ↑ https://www.abcbourse.com/apprendre/12_lecon_af_10_partie2.html
- ↑ https://www.abcbourse.com/apprendre/12_lecon_af_10_partie2.html
- ↑ https://www.cbanque.com/placement/versement_periodique.php
- ↑ https://larevolutionpasteque.com/les-taux-dinteret-le-prix-du-temps/









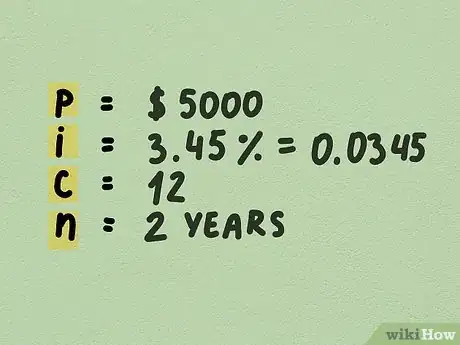
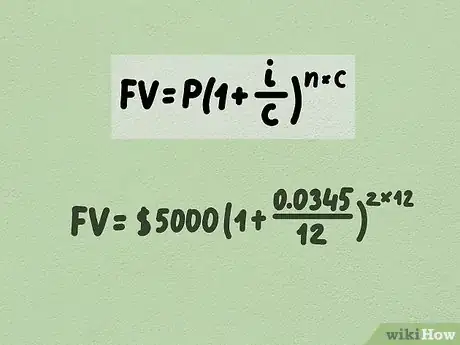







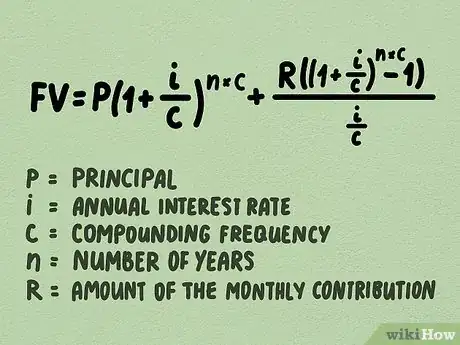


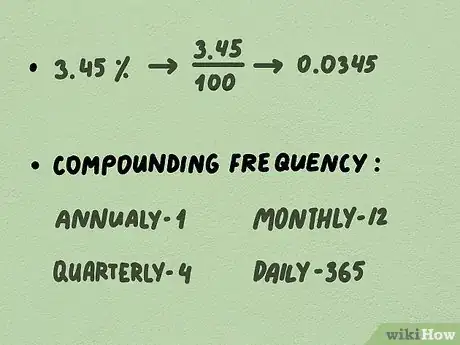
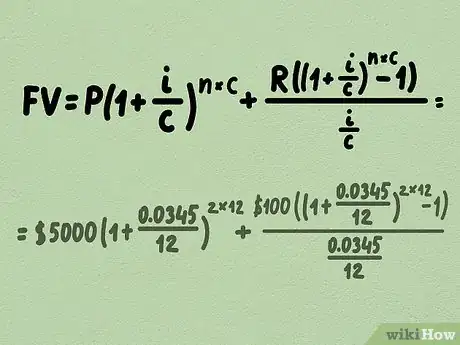













-Step-20-Version-5.webp)