Comment convertir un nombre décimal au format binaire IEEE 754

Informations concernant l'auteur.e

Les ordinateurs fonctionnent sur la base d'un système binaire qui n'accepte que des 0 et des 1 : c'est la base 2. Tout entier naturel en base 10 a son équivalent en base 2. Mais comment font les ordinateurs quand ils ont à traiter, et cela arrive souvent, des nombres décimaux (comme 7,54) ? C'est là qu'intervient le format IEEE 754 qui, sur une base 2, permet de tout convertir, la partie, entière et la partie décimale. Précision : ce format se présente en deux versions, la simple et la double précision.

Pour cette conversion, vous devez maitriser un tant soit peu la conversion de la base 10 vers la base 2. Si besoin était, cet article devrait vous y initier ou vous aider à rafraichir vos connaissances.

Étapes

1
Choisissez le format de la norme IEEE 754. Deux formats sont possibles : le simple et la double précision. Quelle que soit la précision adoptée, la conversion s'opère de la même façon, seul change le traitement de l'exposant et de la mantisse.
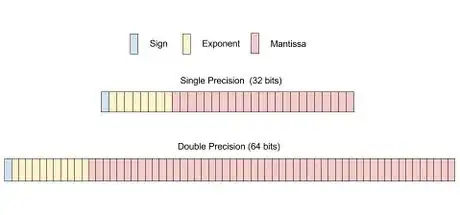
- Sachez ce qu'est la simple précision. Dans la représentation en virgule flottante, chaque chiffre (0 ou 1) est considéré comme 1 bit. Elle utilise 32 bits qui se répartissent de la façon suivante : 1 bit pour le signe de la mantisse, 8 pour l'exposant et 23 pour la mantisse, ce qui fait bien un total de 32 bits (1 + 8 + 23 = 32).
- En double précision (64 bits), le principe est le même avec les trois champs, simplement le nombre de bits alloués à deux d'entre eux est plus important. Elle utilise donc 64 bits qui se répartissent de la façon suivante : 1 bit pour le signe de la mantisse, 11 pour l'exposant et 52 pour la mantisse (1 + 11 + 52 = 64).
- Pour appuyer nos dires, nous chercherons à convertir 85,125 en format IEEE 754 simple précision.
2
Distinguez les parties entière et décimale de votre nombre. C'est la première étape (simple) de la conversion : traiter différemment la partie entière et la partie décimale. Pour plus de clarté, nous partons donc du nombre réel 85,125, dont la partie entière est 85 et la partie décimale 0,125.
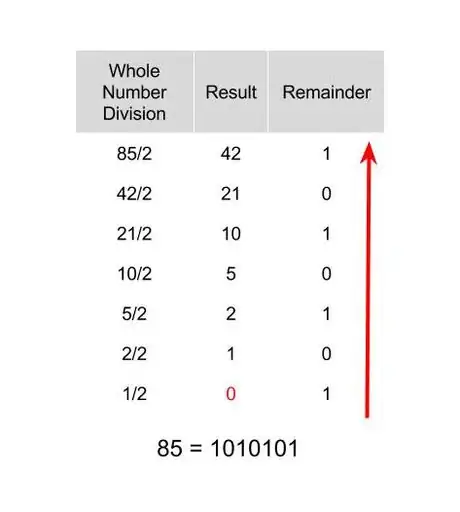
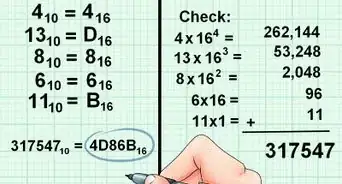
3
Convertissez la partie entière en système binaire ^{[1]
X
Source de recherche}. Comme vous le voyez sur l'illustration, la conversion de 85 en base 2 donne : 1010101.
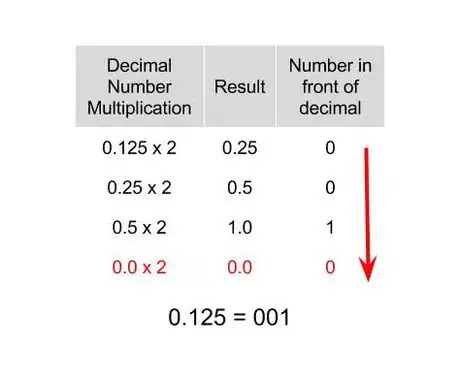
4
Convertissez la partie décimale en système binaire ^{[2]
X
Source de recherche}. Au lieu de diviser le résultat par 2, vous le multipliez par 2 et vous ne gardez que le reste. Il s'agit donc de convertir ici 0,125 en base 2, soit 0,001.
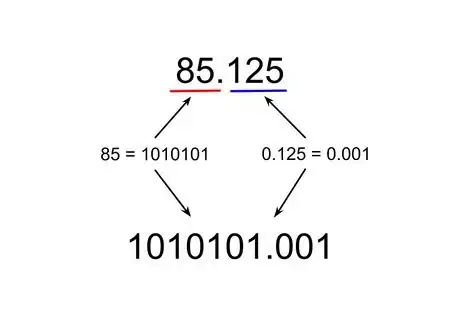
5
Recombinez les deux parties du nombre. Les deux ayant été converties en système binaire, la chose est possible ^{[3]
X
Source de recherche}. Ainsi, en système binaire, 85 s'écrit 1010101 et la partie décimale, 0,001. Les deux parties sont accolées et séparées par une virgule, ce qui donne : 85,125₁₀ = 1010101,001₂.
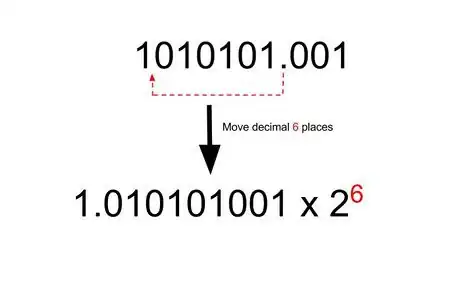
6
Récrivez le nombre en base 2 en notation scientifique. La première étape consiste à déplacer la virgule vers la gauche et à la mettre juste après le premier chiffre. Comme aucun nombre en base 2 ne commence par 0, la virgule est toujours après le premier 1. La seconde étape consiste à rétablir l'équilibre en multipliant ce nouveau nombre par une puissance de 2 dont l'exposant est le nombre de déplacements de la virgule ^{[4]
X
Source de recherche}.
- Ici, nous avons un exposant positif, car la virgule a été déplacée vers la gauche, il aurait été négatif en cas de déplacement vers la droite (chiffre décimal compris entre 0 et 1)
- Dans notre exemple, nous avons donc déplacé la virgule de 6 rangs vers la gauche, si bien que 85,125 s'écrit en notation scientifique de la façon suivante :
  $1,010101001\times 2^{6}$ .
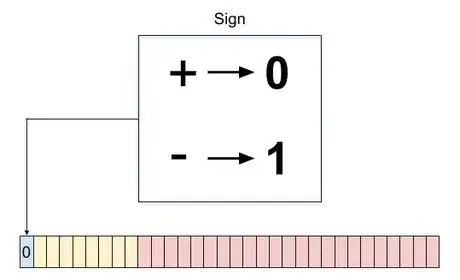
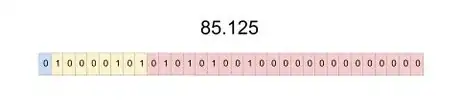
7
Déterminez le signe du nombre. Un nombre est soit négatif soit positif et cela doit se traduire en format IEEE 754. Par convention, si le nombre est positif, le premier bit sera 0 et s'il avait été négatif, il aurait été 1 ^{[5]
X
Source de recherche}. Notre nombre qui sert d'exemple, 85,125, est positif, le premier bit est donc 0. Ce chiffre sera le premier des 32 bits qui serviront à représenter 85,125 en format IEEE 754 (simple précision).
8
Transformez l'exposant en fonction de la précision. Ce format IEEE 754 existe en version simple précision (32 bits) et double (64 bits). Chaque précision a un biais (excédent) que l'on ajoute à l'exposant. En simple précision, l'exposant est codé avec un biais de 127, ce qui dans notre cas doit être ajouté à l'exposant 6 trouvé, soit 127 + 6 = 133.
- La double précision comme son nom le laisse supposer, permet d'écrire des nombres très grands ou au contraire très petits. En double précision, l'exposant est codé avec un biais de 1023. Si nous avions adopté cette précision, nous aurions non pas ajouté 127, mais 1023, ce qui nous aurait donné un exposant de 1029 (1023 + 6).
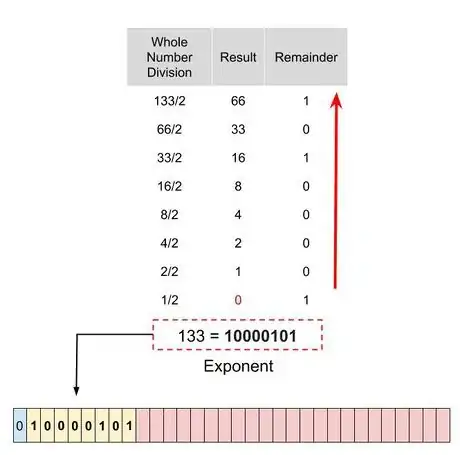
9
Convertissez l'exposant en base 2. Vous avez compris la logique : tout doit être converti en base 2, exposant compris. Ce nombre constituera la deuxième partie du nombre en format IEEE 754. Dans notre exemple, convertissez l'exposant 133 en base 2, soit 10000101.
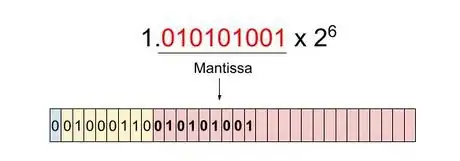
10
Déterminez la mantisse. La mantisse, troisième partie de tout nombre écrit en format IEEE 754, est la partie qui, en notation scientifique, suit la virgule. Comme il y a 23 bits pour cette mantisse, vous ne devez récupérer que les 23 premiers chiffres. Ici, aucune conversion à faire, il faut juste relever les 23 chiffres. Dans notre exemple, la mantisse est la suivante : $010101001(1,{\underline {010101001}}\times 2^{6})$ .
11
Mettez bout à bout les trois éléments trouvés.
- Voilà ! Tout est prêt, car tout est en base 2. En format IEEE 754, tout nombre commence par le signe du nombre converti, 0 ou 1. Lors de la 7^e étape, nous avons dit que le bit du signe était 0, car 85,125 est positif.
- Dans la 9^e étape de cet article, nous avons déterminé les 8 bits de l'exposant en trouvant pour 85,125 un exposant de 10000101.
- Et dans la 10^e étape, nous avons simplement récupéré la mantisse, toute cette partie du nombre en notation scientifique, qui vient juste après la virgule. Nous avons donc précédemment écrit que la mantisse était 010101001.
- Pour finir, il suffit de mettre bout à bout ces trois éléments, signe, exposant et mantisse. Au cas où la mantisse ne comprendrait pas 23 chiffres, vous complèteriez avec des 0, et au cas où il y aurait une séquence (du type 0011 0011…), vous ne prendriez que les 23 premiers chiffres.
- Dans notre exemple, 85,125 converti en format IEEE 754 équivaut à
  0 10000101 01010100100000000000000.
Publicité