Comment lire en binaire

Informations concernant l'auteur.e

Essayer de lire une séquence binaire composée de 1 et 0 peut paraître une tâche impossible. Avec un peu de logique, ça devient facile à comprendre. Les Hommes ont facilement intégré le système de comptage à 10 chiffres, simplement parce que nous avons 10 doigts. D’un autre côté, l’ordinateur a seulement deux « doigts » : les positions on et off, ou 0 et 1, ce qui a donné un système à deux chiffres, soit le système binaire.

Méthode 1

Méthode 1 sur 3:
Avec les exposants

1
Choisissez un nombre binaire que vous voulez convertir. Nous allons prendre par exemple : 101010.
2
Multipliez chaque chiffre binaire par 2 à la puissance de son rang. Rappelez-vous que le binaire se lit de droite à gauche. Le chiffre le plus à droite est considéré comme un 0.
3
Faites la somme de toutes les valeurs. En allant de la droite vers la gauche :
- 0 × 2⁰ = 0
- 1 × 2¹ = 2
- 0 × 2² = 0
- 1 × 2³ = 8
- 0 × 2⁴ = 0
- 1 × 2⁵ = 32
- Total = 42
Publicité

Méthode 2

Méthode 2 sur 3:
Format alternatif avec exposants

1
Choisissez un nombre binaire que vous voulez convertir. Nous allons prendre par exemple : 101. Voici une légère variante de la méthode précédente. Vous trouverez peut-être ce format plus facile à comprendre.
- 101= (1X2) puissance 2 + (0X2) puissance 1 + (1X2) puissance 0
- 101= (2X2) + (0X0) + (1)
- 101= 4 + 0 + 1
- 101= 5
  - Notez que le 'zéro' n’est pas un nombre, mais il faut noter sa valeur.

Méthode 3

Méthode 3 sur 3:
Les valeurs des cases

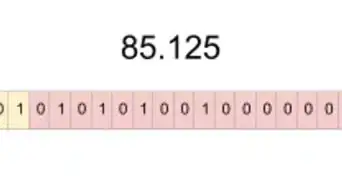
1
Choisissez un nombre binaire. Par exemple 00101010.
2
Lisez de droite à gauche. À chaque case, les valeurs doublent. Donc le premier chiffre à partir de la droite est le 1, le second est un 2, le troisième est un 4, et ainsi de suite.
3
Faites la somme des valeurs « oui ». Les zéros prennent la valeur correspondante, mais ne sont pas additionnés.
- Ainsi, dans notre exemple, cela nous donne : 2 + 8 + 32, pour un résultat de 42.
  - Le 1 équivaut à un « non », le 2 à un « oui », le 4 à un « non », le 8 à un « oui », le 16 à un « non », le 32 à un « oui », le 64 à un « non » et le 128 à un « non ». Vous devez additionner les « oui » et sauter les « non ». Vous pouvez vous arrêter au dernier chiffre.
4
Sachez que le nombre obtenu peut être transformé en une lettre ou une ponctuation.
- En termes de ponctuations, le 42 équivaut à un astérisque (*). Cliquez ici pour consulter un tableau.
Publicité

Conseils

Les règles de calcul habituelles fonctionnent aussi pour les nombres binaires. Le chiffre le plus à droite incrémente un à un jusqu’à ce qu’il ait atteint son maximum (de 0 à 1) puis le chiffre suivant incrémente un à un et on reprend à zéro.
Les nombres que nous avons utilisés aujourd’hui respectent la notation positionnelle. Supposons que nous utilisons des entiers, le chiffre le plus à droite représente les unités, le suivant celui des dizaines et puis celui des centaines, et ainsi de suite. La notation positionnelle pour les nombres binaires commence par le un, deux, quatre, huit, etc.