Simetría (geometría)

Desde el punto de vista geométrico, un objeto posee simetría si existe una "operación" o "transformación" (como una isometría o una transformación afín) capaz de aplicar su figura sobre sí misma. De forma análoga, se dice que el objeto es simétrico porque posee una invarianza con respecto a la transformación.[1]

Letras mayúsculas agrupadas según sus simetrías:
- Simetría vertical (ejes rojos)
- Simetría horizontal (ejes azules)
- Simetría central (puntos rosas)
- Sin simetría (quirales)
Un dibujo de una mariposa con simetría bilateral: los lados izquierdo y derecho son imágenes especulares entre sí con respecto a la línea de puntos, su eje de simetría

Por ejemplo, un círculo girado alrededor de su centro tendrá la misma forma y tamaño que el círculo original: todos los puntos antes y después de la transformación serían indistinguibles. En consecuencia, se dice que un círculo es simétrico por rotación o que posee simetría rotacional. Si la isometría es el reflejo de una figura geométrica, se dice que la figura tiene un eje de simetría; además, es posible que una figura u objeto tenga más de un eje de simetría.[2]

Los tipos de simetrías que son posibles para una figura dependen del conjunto de transformaciones geométricas disponibles y de qué propiedades del objeto deban permanecer sin cambios después de una transformación. Debido a que la composición de dos transformaciones también es una transformación, y que cada transformación tiene una transformación inversa que la deshace, el conjunto de transformaciones respecto a las que un objeto es simétrico forma un grupo matemático, el grupo de simetría del objeto.[3]

Simetrías euclídeas en general

El grupo más común de transformaciones aplicadas a los objetos se denomina grupo euclídeo de "isometrías", que son transformaciones que conservan la distancia relativa entre sus puntos, comúnmente consideradas en el espacio bidimensional o tridimensional (es decir, en la geometría del plano o en la geometría del espacio).

Estas isometrías consisten en reflexiones, rotaciones, traslaciones y combinaciones de estas tres operaciones básicas.[4] En una transformación isométrica, se dice que una figura es simétrica si, después de la transformación, es indistinguible del objeto original antes de la transformación. De forma general, un objeto geométrico es simétrico solo bajo un subconjunto o "subgrupo" de todas las isometrías posibles.

A continuación se describen los tipos de subgrupos de isometría, seguidos por otros tipos de grupos de transformación y por los tipos de invariancia posibles.

Isometrías básicas por dimensión
1D 2D 3D 4D
Número de Reflexiones PuntoAfinidad PuntoAfinidad PuntoAfinidad PuntoAfinidad
1 Reflexión Reflexión Reflexión Reflexión
2 Traslación RotaciónTraslación RotaciónTraslación RotaciónTraslación
3 Trasreflexión Rotorreflexión Trasreflexión Rotorreflexión Trasreflexión
4 Rototraslación Doble rotaciónRototraslación
5 Rototrasreflexión

En esta tabla se presentan las distintas posibilidades de simetría habituales en espacios euclídeos de distinta dimensión y sus combinaciones. En las columnas "Punto" y "Afinidad" se distingue el elemento de referencia de cada transformación. Por ejemplo, en el caso de las reflexiones, una reflexión respecto a un punto (que produce una simetría como la de la letra "S"), es distinta a una simetría por afinidad (que produce una simetría bilateral respecto a un eje, como la que posee la letra "T"). Las "rotaciones" siempre se consideran respecto a un punto (el punto de giro), y las "traslaciones" son siempre transformaciones afines, puesto que implican desplazar formas paralelamente a sí mismas (por ejemplo, una cadena ilimitada de la misma letra repetida, poseería este tipo de simetría, denominada traslacional).

Las combinaciones de estos tres elementos se denominan combinando sus nombres, conservando solo el último sin abreviar. Así, por ejemplo, cuando se menciona una "rototrasreflexión", se está haciendo referencia a la combinación de una rotación, de una traslación y de una reflexión. En el caso de las 4 dimensiones, se produce la "doble rotación", una característica de este espacio que permite introducir dos rotaciones totalmente independientes entre sí. A medida que aumenta el número de dimensiones, se incrementa gradualmente el número de transformaciones posibles.

Según el teorema de Cartan-Dieudonné, una transformación ortogonal cualquiera en un espacio n dimensional, puede representarse por la composición de a lo sumo n reflexiones.

Simetría de reflexión

Se denomina simetría especular, simetría lineal, simetría de reflexión, simetría respecto a un espejo o simetría bilateral, a la simetría generada mediante una reflexión.[5]

En una dimensión, hay un punto de simetría sobre el que tiene lugar la reflexión; en dos dimensiones la simetría se refiere a un eje; y en tres dimensiones, se habla de un plano de simetría.[6] Una figura para la que cada uno de sus puntos se aplican uno a uno sobre otro punto de la figura, equidistantes y en lados opuestos de un plano común, se dice que posee simetría especular (véase imagen especular).

El eje de simetría de una figura bidimensional es una línea tal que, si se construye una recta perpendicular, cualquiera de los dos puntos que se encuentran en la perpendicular a distancias iguales del eje de simetría son idénticos entre sí. Otra forma de pensarlo es que si la forma se doblara por la mitad sobre el eje, las dos mitades serían idénticas: cada mitad es la imagen reflejada de la otra. Por lo tanto, un cuadrado tiene cuatro ejes de simetría, porque hay cuatro formas diferentes de doblarlo y hacer que todos sus lados coincidan. Por el mismo motivo, una circunferencia tiene infinitos ejes de simetría que pasan por su centro.[7]

Si la letra "T" se refleja respecto a un eje vertical, conserva exactamente la misma forma. Esto a veces se llama simetría vertical. Se puede utilizar una formalización más precisa, como por ejemplo afirmando que "T tiene un eje de simetría vertical" o que "T tiene simetría de izquierda a derecha".

Los triángulos con simetría de reflexión son triángulos isósceles, los cuadrilátero con esta simetría son el deltoide y los trapecios isósceles.[8]

Para cada línea o plano de reflexión, el grupo de simetría es isomorfo con Cs (véase grupo puntual en tres dimensiones), uno de los tres tipos de orden dos (involuciones), y por lo tanto algebraicamente isomorfo a C2. Su dominio fundamental es un semiespacio.[9]

Simetría central y otras isometrías involutivas
En 2 dimensiones, una reflexión respecto a un punto equivale a una rotación de 180 grados

La simetría de reflexión se puede generalizar a otras isometrías de un espacio m-dimensional, resultando las correspondientes involuciones, como

(x1, ..., xm) ↦ (−x1, ..., −xk, xk+1, ..., xm)

en un determinado sistema de coordenadas cartesianas. Este cambio de signo de una coordenada implica la reflexión en un espacio afín (m−k)-dimensional.[10] Si k = m, dicha transformación se conoce como simetría central, o una inversión a través de un punto. En el plano (m = 2) un punto de reflexión es lo mismo que una rotación de media vuelta (180°). La simetría antípoda es un nombre alternativo para una simetría de reflexión puntual a través del origen.[11]

Dicha "reflexión" conserva la orientación si y solo si k es un número par.[12] Esto implica que para m = 3 (así como para otros m impares) un punto de reflexión cambia la orientación del espacio, como lo hace una simetría especular. Por eso, en física, el término "P-simetría" se usa tanto para la reflexión puntual como para la simetría especular (P significa paridad). Como un punto de reflexión en tres dimensiones convierte sistemas de coordenadas cartesianas con orientación horaria en sistemas de coordenadas cartesianas con orientación antihoraria, la simetría bajo un punto de reflexión también se denomina simetría izquierda-derecha.[13]

Simetría rotacional
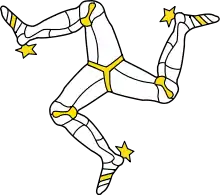
Un trisquel tiene simetría rotacional de 3-lóbulos

La simetría rotacional se verifica con respecto a algunas o a todas las rotaciones en el espacio euclídeo m-dimensional. Las rotaciones son isometrías directas; es decir, isometrías que preservan la orientación.[14] Por lo tanto, un grupo de simetría rotacional es un subgrupo del grupo euclídeo especial E+(m).

La simetría con respecto a todas las rotaciones sobre todos los puntos implica la simetría traslacional (porque las traslaciones son composiciones de rotaciones sobre puntos distintos),[15] y el grupo de simetría es todo el E+(m). Esto no se aplica a los objetos, porque hace que el espacio sea homogéneo, pero puede aplicarse a las leyes físicas.

Para la simetría de las rotaciones respecto a un punto, se puede tomar ese punto como origen. Estas rotaciones forman el grupo ortogonal SO(m), que puede representarse por el grupo de matrices ortogonales de orden m × m con determinante 1. Para m = 3 este es el grupo de rotación SO(3).[16]

En otras palabras, el grupo de rotación de un objeto es el grupo de sus simetrías dentro de E+(m); es decir, el grupo de movimientos rígidos;[17] o lo que es lo mismo, la intersección del grupo de simetría completo con el grupo de movimientos rígidos. Para los objetos quirales (que no poseen simetría alguna), coincide con el grupo de simetría completo.

Las leyes de la física son invariantes con respecto a SO(3) si no se distinguen las diferentes direcciones del espacio. Debido al teorema de Noether, la simetría rotacional de un sistema físico es equivalente a la ley de conservación del momento angular.[18] Véase también el artículo dedicado a la invarianza rotacional.

Simetría traslacional
Un friso, dotado de simetría traslacional

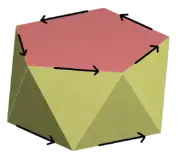
La simetría traslacional deja un objeto invariante en un grupo discreto o continuo de traslaciones .[19] La ilustración de la derecha muestra cuatro triángulos congruentes generados por las traslaciones en el sentido de la flecha. Si la línea de triángulos se extendiera hasta el infinito en ambas direcciones, se tendría una simetría traslacional discreta; cualquier traslación que asigne un triángulo a otro dejaría la línea entera sin cambios.

Simetría de reflexión con deslizamiento
Un friso con simetría deslizada

En 2D, una simetría de reflexión deslizada (en 3D se llama simetría respecto a un plano de deslizamiento, o en general, una transflexión) significa que una reflexión respecto a una línea o plano combinada con una traslación paralela a la línea o plano de simetría, da como resultado el mismo objeto.[20] La composición de dos reflexiones planas da como resultado una simetría de traslación con el vector de traslación duplicado. El grupo de simetría que comprende reflexiones de deslizamiento y traslaciones asociadas es el friso p11g, y es isomorfo con el grupo cíclico infinito Z.

Simetría de rotorreflexión
Un antiprisma pentagonal con sus aristas marcadas muestra simetría rotorreflexiva, con orden 10

En 3D, una reflexión giratoria, rotorreflexión o rotación impropia, consiste en una rotación sobre un eje combinada con la reflexión en un plano perpendicular a ese eje.[21] Los grupos de simetría asociados con las rotorreflexiones incluyen:

  • Si el ángulo de rotación no tiene un divisor común con 360°, el grupo de simetría no es discreto
  • Si la rotorreflexión tiene un ángulo de rotación de 2n lóbulos (es decir, un ángulo de 180°/n), el grupo de simetría es S2n de orden 2n (no debe confundirse con los grupos simétricos, para los que se usa la misma notación; el grupo abstracto es C2n). Un caso especial es n = 1, una inversión, ya que no depende del eje ni del plano, y se caracteriza solo por el punto de inversión.
  • El grupo Cnh (ángulo de 360°/n); para n impar es generado por una sola simetría, y el grupo abstracto es C2n. Para n par, no es una simetría básica, sino una combinación de distintas operaciones.

Simetría helicoidal
Véase también: Eje helicoidal

En geometría 3D y superior, un eje helicoidal (o traslación rotativa) es la combinación de una rotación y de una traslación en el sentido del eje de rotación.[22]

La simetría helicoidal es el tipo de simetría que se ve en objetos cotidianos como resortes, sacacorchos, brocas o barrenas. El concepto de simetría helicoidal se puede visualizar como el trazado en el espacio tridimensional que resulta de rotar un objeto a una velocidad angular constante mientras se desplaza simultáneamente a una velocidad lineal constante paralelamente a su eje de rotación. En cualquier instante, estos dos movimientos se combinan para dar un "ángulo de arrollamiento" que ayuda a definir las propiedades de la hélice recorrida. [23] Cuando el objeto gira rápidamente y se traslada lentamente, el ángulo de enrollamiento estará cerca de 0°. A la inversa, si la rotación es lenta y la traslación es rápida, el ángulo de enrollamiento se aproximará a 90°.

Un helicoide continuo

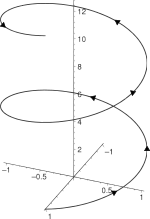
Se pueden distinguir tres clases principales de simetría helicoidal, en función de la interacción del ángulo de las simetrías de enrollado y de traslación respecto al eje:

Un apeirógono oblicuo regular tiene una simetría discreta axial-helicoidal (aquí con 3-lóbulos), dibujado en perspectiva
La hélice de Boerdijk-Coxeter, construida por tetraedros regulares aumentados, es un ejemplo de una simetría axial helicoidal que no es periódica
  • Simetría helicoidal infinita: Si no hay características distintivas sobre un helicoide o sobre un objeto similar a una hélice, el objeto tendrá una simetría infinita, como la de un círculo, pero con el requisito adicional de la traslación a lo largo del eje del objeto para devolverlo a su apariencia original.[24] Un objeto similar a una hélice es uno que posee en cada punto el ángulo regular de enrollamiento de una hélice, pero que también puede tener una sección transversal de complejidad indefinidamente alta, con la condición de que exista exactamente la misma sección transversal (generalmente después de una rotación) en cada punto correspondiente a lo largo del objeto. Los ejemplos simples incluyen resortes enrollados uniformemente, tornillos, brocas y sinfines. Dicho de manera más precisa, un objeto tiene infinitas simetrías helicoidales si para cualquier pequeña rotación del objeto alrededor de su eje central existe un punto cercano (la distancia de traslación) en ese eje en el que el objeto aparecerá exactamente como lo hizo antes. Es esta simetría helicoidal infinita la que da lugar a la curiosa ilusión de movimiento en la longitud de un tornillo sinfín o broca que se está girando. También proporciona la capacidad útil mecánicamente de tales dispositivos para mover materiales en su longitud, siempre que se combinen con una fuerza tal como la gravedad o la fricción.
  • Simetría helicoidal de n-lóbulos: Si el requisito de que todas las secciones transversales del objeto helicoidal sean idénticas se rebaja, es posible que haya simetrías helicoidales menores adicionales. Por ejemplo, la sección transversal del objeto helicoidal puede cambiar, pero aún se repite de manera regular en el eje del objeto helicoidal. En consecuencia, los objetos de este tipo mostrarán una simetría después de una rotación por algún ángulo fijo θ y una traslación por alguna distancia fija, pero en general no serán invariantes para ningún ángulo de rotación. Si el ángulo (rotación) en el que se produce la simetría se divide uniformemente en un círculo completo (360°), el resultado es el equivalente helicoidal de un polígono regular. Este caso se llama simetría helicoidal n-lóbulos, donde n = 360°; por ejemplo, una doble hélice. Este concepto puede generalizarse aún más para incluir casos en los que es un múltiplo de 360°, es decir, el ciclo finalmente se repite, pero solo después de más de una rotación completa del objeto helicoidal.
  • Simetría helicoidal no repetitiva: Este es el caso en el que el ángulo de rotación θ requerido para observar la simetría es irracional. El ángulo de rotación nunca se repite exactamente, sin importar cuántas veces se gire la hélice. Estas simetrías se crean utilizando un Grupo puntual en dos dimensiones no repetitivo. El ácido desoxirribonucleico, con aproximadamente 10.5 pares de bases por vuelta, es un ejemplo de este tipo de simetría helicoidal no repetitiva.[25]

Doble simetría de rotación
Un toro de Clifford 4D, proyectado estereográficamente en 3D, parece un toro. Una doble rotación puede verse como una trayectoria helicoidal
Véase también: Rotaciones en el espacio euclídeo 4-dimensional

En 4D, se puede generar una simetría de doble rotación, como la compuesta de dos rotaciones ortogonales.[26] Es similar al eje helicoidal en 3D, compuesto por una rotación y una traslación ortogonal.

Simetrías no isométricas

Una definición más amplia de la simetría geométrica permite considerar operaciones incluidas en un grupo más amplio que el grupo euclídeo de isometrías. Ejemplos de grupos de simetría geométrica más grandes son:

Esto agrega, por ejemplo, simetrías oblicuas como el cizallamiento.
Esto agrega, por ejemplo, las reflexiones inversas, como la reflexión respecto a una circunferencia en el plano.

En el Programa de Erlangen, propuesto por el matemático Felix Klein en el siglo XIX, cada grupo posible de simetrías define una geometría en la que los objetos que están relacionados por un miembro del grupo de simetría se consideran equivalentes.[29] Por ejemplo, el grupo euclídeo define la geometría euclídea, mientras que el grupo de transformaciones de Möbius define la geometría proyectiva.

Simetría de escala y fractales
Un conjunto de Julia tiene simetría de escala

La simetría de escala significa que si un objeto se amplía o reduce de tamaño, el nuevo objeto tiene las mismas propiedades que el original.[30] Esto no es cierto en la mayoría de los sistemas físicos, como atestigua la diferencia en la forma de las patas de un elefante y de un ratón (denominada alometría). De manera similar, si una vela de cera se ampliara al tamaño de un árbol alto, inmediatamente colapsaría bajo su propio peso.

Una forma más sutil de simetría de escala esconde en los fractales. Tal como fueron concebidos por Benoît Mandelbrot, los fractales son un concepto matemático en el que la estructura de una forma compleja parece similar independientemente del grado de grado de aumento con el que se contemplen,[31] como es evidente en el conjunto de Mandelbrot. Una línea costera es un ejemplo de un fractal que se produce de forma natural, ya que conserva una complejidad de apariencia similar en todos los niveles, desde la vista de un satélite hasta un examen microscópico de cómo el agua salta contra los granos individuales de arena. La ramificación de los árboles, que permite que las pequeñas ramitas se conviertan en árboles completos en un diorama a escala, es otro ejemplo.

Debido a que los fractales pueden generar la apariencia de patrones en la naturaleza, tienen una belleza y una familiaridad que no se ven normalmente en las funciones generadas matemáticamente. Los fractales también han encontrado un lugar en la generación de efectos visuales digitales, donde su capacidad para crear curvas complejas con simetrías fractales da como resultado un mundo virtual más realista.

Simetría abstracta

Criterio de Klein

Con cada geometría, Felix Klein asociaba un grupo de simetrías subyacente. La jerarquía de geometrías se representa matemáticamente como una ordenación de estos grupos, y de sus invariantes. Por ejemplo, las longitudes, los ángulos y las áreas se conservan con respecto al grupo euclídeo de las simetrías, mientras que solo la estructura incidente y la razón anarmónica se conservan bajo las transformaciones proyectivas con carácter general. El concepto de paralelismo, que se conserva en la geometría afín, no es significativo en la geometría proyectiva. Luego, al abstraer los grupos subyacentes a las simetrías de las distintas geometrías, las relaciones entre ellas se pueden restablecer desde el punto de vista algebraico. Dado que el grupo de geometría afín es un subgrupo del grupo de la geometría proyectiva, cualquier noción invariante en geometría proyectiva es "a priori" propia de la geometría afín; pero no al revés. Si se agregan las simetrías requeridas, se obtiene una teoría más poderosa pero menos conceptos y teoremas (que, eso sí, serán más profundos y más generales).

Criterio de Thurston

William Thurston introdujo una versión similar de simetrías en geometría. Una geometría de modelo es una variedad diferenciable simplemente conexa X junto con una acción transitiva de un Grupo de Lie G en X, con estabilizadores compactos. El Grupo de Lie se puede considerar como el grupo de simetrías de la geometría.

Una geometría de modelo se llama máxima si G es máxima entre los grupos que actúan sin problemas y de forma transitiva en X con estabilizadores compactos, es decir, si es el grupo máximo de simetrías. A veces, esta condición se incluye en la definición de una geometría de modelo.

Una estructura geométrica sobre una variedad M es un difeomorfismo de M a X/Γ para alguna geometría de modelo X, donde Γ es un subgrupo discreto de G actuando libremente sobre X. Si una variedad dada admite una estructura geométrica, entonces admite una cuyo modelo es máximo.

Una geometría modelo tridimensional X es relevante para la conjetura de geometrización si es máxima y si hay al menos una variedad compacta con una estructura geométrica modelada en X. Thurston clasificó las 8 geometrías modelo que satisfacen estas condiciones; se enumeran a continuación y, en ocasiones, se denominan "geometrías de Thurston" (también hay innumerables otras geometrías modelo sin cocientes compactos).

Las ocho geometrías modelo de Thurston
  • Geometría esférica S3
Como la de la 3-esfera, la esfera de Poincaré o los espacios lenticulares.
  • Geometría euclidiana E3
Con ejemplos como el 3-toro. Hay exactamente 10 variedades múltiples cerradas finitas con esta geometría, 6 orientables y 4 no orientables.
  • Geometría hiperbólica H3
Hay un gran número de ejemplos de este tipo, como la variedad de Weeks o el espacio de Seifert-Weber, aunque su clasificación todavía no se ha fijado por completo.
  • Geometría de S2 × R
Existen cuatro variedades finitas volumétricas de este tipo.
  • Geometría de H2 × R
Ejemplos de este tipo incluyen el producto de una superficie hiperbólica por un círculo, o más generalmente, el toro resultante de la aplicación de una isometría sobre una superficie hiperbólica.
  • Geometría del recubrimiento universal de SL(2, R)
En este tipo se incluyen la variedad de vectores unitarios del haz tangente de una superficie hiperbólica, y más generalmente las esferas de homología de Brieskorn (excepto la esfera 3 y el espacio dodecaédrico de Poincare).
  • Geometría nula
Es la geometría del grupo de Heisenberg.
  • Geometría resoluble
El grupo posee 8 componentes, y es el grupo de aplicaciones del espacio de Minkowski bidimensional que son isometrías o multiplican la métrica por −1.

Referencias
  1. Martin, G. (1996). Transformation Geometry: An Introduction to Symmetry. Springer. p. 28.
  2. Freitag, Mark (2013). Mathematics for Elementary School Teachers: A Process Approach. Cengage Learning. p. 721.
  3. Miller, Willard Jr. (1972). Symmetry Groups and Their Applications. New York: Academic Press. OCLC 589081. Archivado desde el original el 17 de febrero de 2010. Consultado el 28 de septiembre de 2009.
  4. «Higher Dimensional Group Theory». Archivado desde el original el 23 de julio de 2012. Consultado el 16 de abril de 2013.
  5. Weyl, Hermann (1982) [1952]. Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3.
  6. Cowin, Stephen C.; Doty, Stephen B. (2007). Tissue Mechanics. Springer. p. 152.
  7. Caldecott, Stratford (2009). Beauty for Truth's Sake: On the Re-enchantment of Education. Brazos Press. p. 70.
  8. Bassarear, Tom (2011). Mathematics for Elementary School Teachers (5 edición). Cengage Learning. p. 499.
  9. Johnson, N. W. Johnson (2018). «11: Finite symmetry groups». Geometries and Transformations. Cambridge University Press.
  10. Hertrich-Jeromin, Udo (2003). Introduction to Möbius Differential Geometry. Cambridge University Press.
  11. Dieck, Tammo (2008). Algebraic Topology. European Mathematical Society. pp. 261. ISBN 9783037190487.
  12. William H. Barker, Roger Howe Continuous Symmetry: From Euclid to Klein (Google eBook) American Mathematical Soc
  13. W.M. Gibson & B.R. Pollard (1980). Symmetry principles in elementary particle physics. Cambridge University Press. pp. 120-122. ISBN 0 521 29964 0.
  14. Vladimir G. Ivancevic, Tijana T. Ivancevic (2005) Natural Biodynamics World Scientific
  15. Singer, David A. (1998). Geometry: Plane and Fancy. Springer Science & Business Media.
  16. Joshi, A. W. (2007). Elements of Group Theory for Physicists. New Age International. pp. 111ff.
  17. Hartshorne, Robin (2000). Geometry: Euclid and Beyond. Springer Science & Business Media.
  18. Kosmann-Schwarzbach, Yvette (2010). The Noether theorems: Invariance and conservation laws in the twentieth century. Sources and Studies in the History of Mathematics and Physical Sciences. Springer-Verlag. ISBN 978-0-387-87867-6.
  19. Stenger, Victor J. (2000) and Mahou Shiro (2007). Timeless Reality. Prometheus Books. Especially chapter 12. Nontechnical.
  20. Martin, George E. (1982), Transformation Geometry: An Introduction to Symmetry, Undergraduate Texts in Mathematics, Springer, p. 64, ISBN 9780387906362..
  21. Robert O. Gould, Steffen Borchardt-Ott (2011)Crystallography: An Introduction Springer Science & Business Media
  22. Bottema, O, and B. Roth, Theoretical Kinematics, Dover Publications (September 1990)
  23. George R. McGhee (2006) The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces Cambridge University Press p.64
  24. Anna Ursyn(2012) Biologically-inspired Computing for the Arts: Scientific Data Through Graphics IGI Global Snippet p.209
  25. Sinden, Richard R. (1994). DNA structure and function. Gulf Professional Publishing. p. 101. ISBN 9780126457506.
  26. Charles Howard Hinton (1906) The Fourth Dimension (Google eBook) S. Sonnenschein & Company p.223
  27. Harold Scott MacDonald Coxeter (1961,9) Introduction to Geometry, §5 Similarity in the Euclidean Plane, pp. 67–76, §7 Isometry and Similarity in Euclidean Space, pp 96–104, John Wiley & Sons.
  28. William Thurston. Three-dimensional geometry and topology. Vol. 1. Edited by Silvio Levy. Princeton Mathematical Series, 35. Princeton University Press, Princeton, NJ, 1997. x+311 pp. ISBN 0-691-08304-5
  29. Klein, Felix, 1872. "Vergleichende Betrachtungen über neuere geometrische Forschungen" ('A comparative review of recent researches in geometry'), Mathematische Annalen, 43 (1893) pp. 63–100 (Also: Gesammelte Abh. Vol. 1, Springer, 1921, pp. 460–497).
    An English translation by Mellen Haskell appeared in Bull. N. Y. Math. Soc 2 (1892–1893): 215–249.
  30. Tian Yu Cao Conceptual Foundations of Quantum Field Theory Cambridge University Press p.154-155
  31. Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.