CW-complexe

Grossièrement, un CW-complexe est obtenu à partir d'un ensemble de 0-cellules, ou « sommets », en recollant successivement des « cellules » fermées (images continues de boules euclidiennes fermées) de dimensions 1, 2, …, le long de leurs bords.

Plus précisément[3]^,[4], une structure de CW-complexe sur un espace X est la donnée d'une suite croissante (X_n) de sous-espaces (X_n est appelé le n-squelette de X) telle que :

• le 0-squelette est un espace discret non vide ;
• pour tout n > 0, le n-squelette est homéomorphe à l'espace obtenu en attachant une famille de n-boules fermées au (n – 1)-squelette, le long de leurs bords (qui sont des (n – 1)-sphères), par le choix d'une application de recollement ;
• les squelettes forment un recouvrement fondamental de X, c'est-à-dire qu'ils recouvrent X et qu'une partie est fermée dans X si et seulement si, pour tout n, son intersection avec le n-squelette X_n est fermée dans X_n (d'où le nom de « topologie faible »).

On démontre qu'alors[5]^,[6] :

• chaque « cellule ouverte » (c'est-à-dire chaque image de l'intérieur d'une boule fermée par l'un des recollements) est canoniquement homéomorphe à la boule ouverte correspondante ;
• les cellules ouvertes et les sommets forment une partition de X ;
• X est séparé ;
• tout compact de X (en particulier toute cellule fermée) ne coupe qu'un nombre fini de cellules ouvertes (d'où le nom de « à fermeture finie »).

Le n-squelette X_n est la réunion des n-cellules fermées de dimensions inférieures ou égales à n. Si X est réduit à X_n, il est dit de dimension n (il est dit de dimension infinie s'il n'est réduit à aucun de ses squelettes). X est dit fini s'il n'a qu'un nombre fini de cellules.

Une réunion fermée de cellules de X est appelée un sous-complexe de X (c'est encore un CW-complexe). Le n-squelette de X est donc le sous-complexe maximum de dimension inférieure ou égale à n.

La définition d'un complexe cellulaire est plus générale en ce qu'elle autorise des recollements de cellules dans un ordre quelconque par rapport aux dimensions, mais tout complexe cellulaire est homotopiquement équivalent à un CW-complexe[7].

La boucle d'oreille hawaïenne n'a pas le type d'homotopie d'un CW-complexe.

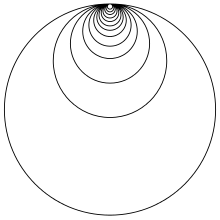
• La structure standard de CW-complexe (de dimension 1) sur la droite réelle a pour 0-squelette l'ensemble ℤ des entiers relatifs et pour 1-cellules les intervalles [n, n + 1] pour n entier. De même, la structure standard sur ℝⁿ, de dimension n, est le réseau qui a des cellules cubiques produits des 0- et 1-cellules de ℝ.
• Tout complexe simplicial, en particulier tout polyèdre ou tout graphe, est naturellement muni d'une structure de CW-complexe. (Les graphes cubiques sont, en un certain sens, les CW-complexes de dimension 1 « génériques ».)^{[réf. nécessaire]} Mais il existe des CW-complexes non triangulables[8].
• La CW-structure la plus simple de la n-sphère Sⁿ a deux cellules : une 0-cellule et une n-cellule, ce qui suffit à décrire le CW-complexe. On peut en construire bien d'autres, en prenant comme (n – 1)-squelette S^{n – 1} (muni de l'une de ses CW-structures, au choix), servant d'équateur, sur lequel on recolle deux hémisphères : deux n-cellules, le long de l'application identité de S^{n – 1}.
• L'espace projectif réel P_n(ℝ) a une CW-structure avec une cellule en chaque dimension inférieure ou égale à n : l'application d'attachement de sa n-cellule à son (n – 1)-squelette P_{n – 1}(ℝ) est la projection canonique, de S^{n – 1} sur son 2-quotient P_{n – 1}(ℝ).
• Les grassmanniennes ont une structure de CW-complexe dont les cellules sont indexées par les symboles de Schubert[9].
• Toute variété différentielle et toute variété algébrique complexe a le type d'homotopie d'un CW-complexe.
• Une variété de Banach de dimension infinie n'est jamais un CW-complexe (car c'est un espace de Baire donc elle ne peut pas s'écrire comme réunion dénombrable de n-squelettes, dont chacun serait un fermé d'intérieur vide) mais lorsqu'elle est métrisable, elle a le type d'homotopie d'un CW-complexe[10].
• L'espace {re^2πiθ | 0 ≤ r ≤ 1, θ ∈ ℚ} ⊂ ℝ² a le type d'homotopie d'un point mais n'a pas de structure de CW-complexe, car il n'est pas localement contractile.
• La boucle d'oreille hawaïenne n'a même pas le type d'homotopie d'un CW-complexe car elle n'est pas semi-localement contractile[11], ni même semi-localement simplement connexe.

• Tout CW-complexe est localement contractile.
• Tout compact d'un CW-complexe X est contenu dans un sous-complexe fini[6] et X est compactement engendré. Il est compact si et seulement s'il est fini[12].
• Tout CW-complexe est paracompact[13] donc normal. Il est même parfaitement normal[14].
• Un CW-complexe est localement compact si et seulement s'il est « localement fini », c'est-à-dire si son recouvrement par les cellules fermées est localement fini, ou encore si toute cellule fermée ne rencontre qu'un nombre fini de cellules fermées, ou si tout point est intérieur à un sous-complexe fini[15]^,[16].
• Un CW-complexe est connexe si et seulement si son 1-squelette l'est. Dans ce cas, il est métrisable si et seulement s'il est localement fini[15].
• Le produit X×Y de deux CW-complexes est le CW-complexe construit sur le produit cartésien de X et Y et dont chaque cellule est le produit d'une cellule de X par une cellule de Y. Sa topologie est celle du produit dans la catégorie des espaces compactement engendrés. Elle est en général plus fine que la topologie produit, mais coïncide avec cette dernière dans les cas les plus courants : il suffit que X ou Y soit fini ou que X et Y soient dénombrables, et il suffit même que ces propriétés soient vérifiées localement[14]^,[17].
• Tout quotient séparé d'un CW-complexe par une relation d'équivalence « cellulaire » est un CW-complexe (par exemple : toute identification d'une réunion de sous-complexes à un point, comme dans le cône ou la suspension, ou même le smash-produit de deux CW-complexes lorsque leur produit en est un). Plus généralement, tout recollement X ∪_f Y d'un CW-complexe sur un autre le long d'une application cellulaire est un CW-complexe[18].
• Tout revêtement d'un CW-complexe est encore un CW-complexe[19].
• Il ne suffit pas que X et Y soient des CW-complexes pour que l'espace C(X, Y) des applications continues de X dans Y (muni de la topologie compacte-ouverte) en soit un. Mais si X et Y ont le type d'homotopie de CW-complexes et si X est compact alors C(X, Y) a le type d'homotopie d'un CW-complexe[20].

La cohomologie et l'homologie singulières des CW-complexes sont aisément calculables via l'homologie cellulaire, qui est une théorie homologique pour la catégorie des CW-complexes et des applications cellulaires. Pour calculer une (co)homologie extraordinaire d'un CW-complexe, la suite spectrale d'Atiyah-Hirzebruch est l'analogue de l'homologie cellulaire.

Exemples choisis parmi les CW-complexes particuliers évoqués plus haut :

• Pour la sphère Sⁿ (n > 0), si l'on choisit la décomposition en seulement une 0-cellule et une n-cellule, le complexe de chaînes cellulaires C_✻ et son homologie sont donnés par :${\displaystyle H_{k}(S^{n})=C_{k}={\begin{cases}\mathbb {Z} &{\text{ si }}k\in \{0,n\},\\0&{\text{ sinon,}}\end{cases}}}$puisque toutes les différentielles sont nulles.
  On trouve bien sûr la même homologie en utilisant, par exemple, la décomposition équatoriale de façon récursive, donc avec deux cellules en chaque dimension de 0 à n, qui donne comme complexe de chaînes${\displaystyle C_{k}={\begin{cases}\mathbb {Z} ^{2}&{\text{ si }}0\leq k\leq n,\\0&{\text{ sinon}}\end{cases}}\quad {\text{et}}\quad \partial _{k}={\begin{pmatrix}1&-1\\1&-1\end{pmatrix}},}$exact sauf en C₀ et en C_n.
• Pour l'espace projectif réel P_n(ℝ), la même méthode donne :${\displaystyle C_{k}={\begin{cases}\mathbb {Z} &{\text{ si }}0\leq k\leq n\\0&{\text{ sinon}}\end{cases}}\quad {\text{et}}\quad \partial _{k}=1+(-1)^{k}:C_{k}\to C_{k-1}\quad }$donc${\displaystyle H_{k}(P_{n}(\mathbb {R} ))={\begin{cases}\mathbb {Z} &{\text{ si }}k=0{\text{ ou si }}k=n{\text{ impair,}}\\\mathbb {Z} _{2}&{\text{ si }}k{\text{ impair }}\in ]0,n[,\\0&{\text{ sinon.}}\end{cases}}}$

Certaines équivalences d'homotopie, dites simples (en)[21], permettent de remplacer un CW-complexe X par un autre, ayant moins de cellules.

Le 1-squelette de X est un graphe. Soit F une forêt (une réunion disjointe d'arbres) maximale dans ce graphe. En notant x ∼ y lorsque x et y sont dans un même arbre de cette forêt, l'application X → X/∼ est une équivalence d'homotopie car les arbres sont contractiles. Le quotient X/∼ est un CW-complexe dont les cellules correspondent aux cellules de X non contenues dans F. En particulier, le 1-squelette de X/∼ est une union disjointe de bouquets de cercles. Par exemple si X était connexe, le 0-squelette de X/∼ sera réduit à un point.

En montant dans l'échelle de connexité, supposons maintenant que X est un CW-complexe simplement connexe dont le 0-squelette est réduit à un point. On peut alors trouver un CW-complexe homotopiquement équivalent dont le 1-squelette est, lui aussi, un singleton. Pour ce faire, on considère X₁ et l'attachement des 2-cellules comme une présentation de groupe et l'on mime les transformations de Tietze (ajouts et retraits de générateurs et de relations, modifiant une présentation sans changer le groupe) par des ajouts et retraits de cellules.

Pour transformer un CW-complexe n-connexe X en un CW-complexe homotopiquement équivalent dont le n-squelette est un singleton, on utilise pour n > 1 les mêmes idées, en remplaçant les transformations de Tietze sur une présentation du groupe fondamental par des opérations élémentaires sur les matrices de présentation du complexe cellulaire de X.

La catégorie homotopique (en) des CW-complexes pointés (ou de leurs variantes ci-dessous) est un cadre adapté pour la théorie de l'homotopie :

• les espaces ayant le type d'homotopie d'un CW-complexe, ou d'un complexe simplicial, ou d'un rétract absolu de voisinage, sont les mêmes[22] ;
• toute inclusion de CW-complexes est une cofibration[23] ;
• approximation cellulaire (en) : toute application continue entre CW-complexes est homotope à une application cellulaire ;
• théorème de Whitehead : pour qu'une application continue entre CW-complexes connexes soit une équivalence d'homotopie, il (faut et il) suffit que les morphismes qu'elle induit sur les groupes d'homotopie soient des isomorphismes ;
• le théorème de représentabilité de Brown (en) donne une caractérisation simple des foncteurs représentables sur cette catégorie.