Système international d'unités

Le Système international d'unités (abrégé en SI), inspiré du système métrique, est le système d'unités le plus largement employé au monde ; il n'est pas officiellement utilisé aux États-Unis, au Liberia et en Birmanie. Il s’agit d’un système décimal (on passe d’une unité à ses multiples ou sous-multiples à l’aide de puissances de 10) sauf pour la mesure du temps et des angles. C’est la Conférence générale des poids et mesures, rassemblant des délégués des États membres de la Convention du Mètre, qui décide de son évolution, tous les quatre ans, à Paris. L’abréviation de « Système international » est SI, quelle que soit la langue utilisée.

Pour les articles homonymes, voir SI, SIU et Système international.

La norme internationale ISO 80000-1:2009 décrit les unités du Système international et les recommandations pour l’emploi de leurs multiples et de certaines autres unités.

Instruments de mesure usuels.

Unités et préfixes

Le Système international d'unités se compose d'un ensemble d'unités de base, d'unités dérivées et de multiplicateurs à base décimale qui sont utilisés comme préfixes[1]. La Conférence générale des poids et mesures, rassemblant des délégués des États membres de la Convention du Mètre, décide de leur évolution, tous les quatre ans, à Paris[2].

La norme internationale ISO 80000-1:2009[3] décrit les unités du Système international et les recommandations pour l’emploi de leurs multiples et de certaines autres unités[4].

Unités de base

Le Système international comporte sept unités de base, destinées à mesurer des grandeurs physiques indépendantes[5] et possédant chacune un symbole :

Grandeur Symbole
de la
grandeur		 Symbole
de la
dimension		 Unité SI Symbole
associé
à l'unité
MassemMkilogrammekg
TempstTsecondes
Longueurl, x, r…Lmètrem
TempératureTΘkelvinK
Intensité électriqueI, iIampèreA
Quantité de matièrenNmolemol
Intensité lumineuseIvJcandelacd

Unités dérivées

Les unités dérivées dans le SI sont formées par les puissances, les produits ou les quotients des unités de base et sont potentiellement illimitées en nombre[1],[6]. Les unités dérivées sont associées à des grandeurs dérivées ; par exemple, la vitesse est une grandeur dérivée des grandeurs de base du temps et de la longueur, et l'unité SI dérivée est donc le mètre par seconde (symbole m/s). Les dimensions des unités dérivées peuvent être exprimées en fonction des dimensions des unités de base.

Des combinaisons d'unités de base et d'unités dérivées peuvent être utilisées pour exprimer d'autres unités dérivées. Par exemple, l'unité SI de force est le newton (N), l'unité SI de pression est le pascal (Pa), qui correspond à un newton par mètre carré (N/m2)[7].

Unités dérivées du SI avec des noms et des symboles spéciaux[6]
Nom Symbole Grandeur En unité SI Alternative
radian[N 1] rad angle m/m 1
stéradian[N 1] sr angle solide m2/m2 1
hertz Hz fréquence s−1
newton N force, poids kg m s−2
pascal Pa pression, contrainte kg m−1 s−2 N/m2
joule J énergie, travail kg m2 s−2 N m = Pa m3
watt W puissance, flux énergétique kg m2 s−3 J/s
coulomb C charge électrique s A
volt V potentiel électrique (tension électrique), f.é.m. kg m2 s−3 A−1 W/A = J/C
farad F capacité électrique kg−1 m−2 s4 A2 C/V
ohm Ω résistance, impédance, réactance kg m2 s−3 A−2 V/A
siemens S conductance électrique kg−1 m−2 s3 A2 Ω−1
weber Wb flux magnétique kg m2 s−2 A−1 V s
tesla T champ magnétique kg s−2 A−1 Wb/m2
henry H inductance kg m2 s−2 A−2 Wb/A
degré Celsius °C θ(°C) = T(K) − 273,15 K
lumen lm flux lumineux cd sr cd sr
lux lx éclairement lumineux cd sr m−2 lm/m2
becquerel Bq radioactivité (désintégrations par seconde) s−1
gray Gy dose absorbée (de rayonnement ionisant) m2 s−2 J/kg
sievert Sv dose équivalente (de rayonnement ionisant) m2 s−2 J/kg
katal kat catalyse mol s−1
Notes
  1. Le radian et le stéradian sont définis comme des unités dérivées sans dimension.

Préfixes

Des préfixes officiels permettent de désigner les unités multiples et sous-multiples d'une unité. Par exemple, le sous-multiple du mètre valant 0,01 m est appelé centimètre (symbole cm) puisque le préfixe correspondant à 10−2 est centi-.

Préfixes du Système international d'unités et noms des nombres correspondants
10n 1 000m
m = n/3		 Préfixe
français		 Symbole Depuis
[alpha 1]		 Nombre décimal Désignation
Échelle longue[alpha 2] Échelle courte
1024 1 0008 yotta Y 1991 1 000 000 000 000 000 000 000 000 Quadrillion Septillion
1021 1 0007 zetta Z 1991 1 000 000 000 000 000 000 000 Trilliard Sextillion
1018 1 0006 exa E 1975 1 000 000 000 000 000 000 Trillion[8] Quintillion
1015 1 0005 péta P 1975 1 000 000 000 000 000 Billiard Quadrillion
1012 1 0004 téra T 1960 1 000 000 000 000 Billion[8] Trillion
109 1 0003 giga G 1960 1 000 000 000 Milliard Billion
106 1 0002 méga M 1960 1 000 000 Million
103 1 0001 kilo k 1795 1 000 Millier
102 1 0002/3 hecto h 1795 100 Centaine
101 1 0001/3 déca da 1795 10 Dizaine
100 1 0000 (aucun) — — 1 Unité
10−1 1 000−1/3 déci d 1795 0,1 Dixième
10−2 1 000−2/3 centi c 1795 0,01 Centième
10−3 1 000−1 milli m 1795 0,001 Millième
10−6 1 000−2 micro µ 1960[alpha 3] 0,000001 Millionième
10−9 1 000−3 nano n 1960 0,000 000 001 Milliardième[8] Billionième
10−12 1 000−4 pico p 1960 0,000 000 000 001 Billionième Trillionième
10−15 1 000−5 femto f 1964 0,000 000 000 000 001 Billiardième Quadrillionième
10−18 1 000−6 atto a 1964 0,000 000 000 000 000 001 Trillionième Quintillionième
10−21 1 000−7 zepto z 1991 0,000 000 000 000 000 000 001 Trilliardième Sextillionième
10−24 1 000−8 yocto y 1991 0,000 000 000 000 000 000 000 001 Quadrillionième Septillionième

Règles orthographiques et typographiques

Les principes de l'écriture des nombres, des grandeurs, des unités et des symboles forment ce que l'on peut appeler la « grammaire » du Système international d'unités. Les références normatives sont le Bureau international des poids et mesures[9], la norme internationale ISO 80000-1:2009[10] et, en France, le fascicule de documentation de l'AFNOR : FD X 02-003 de [11].

Les unités ne peuvent être désignées que par leur nom (pouvant varier d'une langue à une autre), ou par leur symbole (international, indépendant de la langue). Il ne faut pas mélanger les symboles et les noms des unités. On écrit, correctement, « newton par kilogramme » ou N/kg mais jamais « newton par kg », « newton/kg », « newton/kilogramme », ni « km/heure ». Sont prohibées les abréviations telles que « sec » pour la seconde (s), « mn » pour la minute (min) ou « cc » pour le centimètre cube (cm3).

Les symboles des unités (mais pas leurs noms) commencent par une majuscule[12] si le nom de l'unité provient d'un nom propre, et une minuscule dans le cas contraire[12],[13]. Ainsi, on peut comparer les symboles du pascal (Pa) et de la seconde (s). La seule exception à cette règle est le symbole du litre, qui peut s'écrire au choix « l » ou « L », pour éviter les confusions[14] avec le chiffre 1 ou la lettre i majuscule (I) selon les polices de caractères utilisées. Les symboles des unités sont toujours écrits en caractères romains[12] quelle que soit la police du texte où ils figurent : ils ne sont pas mis en italique ; ils sont grammaticalement invariables et ne sont pas suivis d'un point (sauf nécessité typographique, par exemple en fin de phrase)[12].

Toutes les unités, toujours à droite de la valeur, sont par convention séparées de la valeur par une espace insécable, exceptions faites des symboles des unités sexagésimales d'angle, par exemple : 40° 16′ 25″ (symboles prime ′ pour les minutes et double prime ″ pour les secondes) et des degrés d'alcool, par exemple : alcool à 90°[15]). Ainsi, on écrit « 30 cm » mais pas « 30cm » ; de même, on écrit « 30,2 °C » mais pas « 30,2°C » ni « 30,2 ° C », le symbole °C étant composé du « ° » et du « C » qui sont, eux deux, indissociables.

Le nom des unités écrit en entier est quant à lui un nom commun : même si l'unité dérive d'un nom propre, la première lettre du nom d'une unité est donc toujours une minuscule (contrairement à son symbole) ; en toutes lettres, le nom d'une unité prend la marque du pluriel. On écrit ainsi « trois ampères », « deux teslas ».

Note : contrairement au cas du kelvin, le nom du degré Celsius (°C) est composé, c'est alors la première lettre du mot « degré » qui prend la minuscule et la marque du pluriel. On écrit ainsi « deux degrés Celsius ».

Les notations de la division et de la multiplication s'appliquent aux symboles des unités dérivées. Ainsi on peut écrire le symbole du mètre par seconde m⋅s-1 ou m/s et celui du kilowatt-heure kWh ou kW⋅h. Lorsque deux unités sont multipliées, on utilise, entre les symboles, un point à mi-hauteur centré [⋅][alpha 4] ou par une espace, pour distinguer certains préfixes de symboles d'unités. En ce qui concerne la division, tout ce qui est affecté d'un exposant négatif est énoncé à la suite de la barre oblique ou du mot « par » : ainsi, l'unité SI de vitesse est le mètre par seconde (m/s), la forme « mètre seconde » étant incorrecte (elle désignerait le produit d'une distance par une durée). Pour éviter les notations ambiguës, on n'utilise jamais plus d'une barre oblique dans le symbole d'une unité (A/m/s, qui correspond à l'ampère par mètre par seconde, A⋅m-1⋅s-1, pourrait être pris pour A/(m/s), qui correspond à l'ampère seconde par mètre, A⋅s⋅m-1 ou A⋅s/m)[16]. Ainsi la conductivité thermique s'exprime par le watt mètre par mètre carré kelvin, W ⋅ m/(m2 ⋅ K), ou par le watt par mètre kelvin, W/(m ⋅ K).

En cas de produit d'unités, on utilise dans le nom de l'unité dérivée un tiret ou une espace. Ainsi, les bonnes orthographes de l'unité dont le symbole est kWh sont « kilowatt-heure » et « kilowatt heure »[16]. Dans ces deux cas, chacun des noms d'unités prend la marque du pluriel : kilowatts-heures ou kilowatts heures. En l'absence de trait d'union ou d'espace, seul le deuxième nom d'unité prend la marque du pluriel : wattheures, voltampères. Quand une même unité entre plusieurs fois dans un produit, on peut l'énoncer en faisant suivre son nom, selon le cas, des adjectifs « carré », « cube » ou « bicarré », ou des expressions « au carré », « au cube » ou « à la puissance n » :

  • mètre carré, symbole m2 ; pluriel : mètres carrés ;
  • mètre cube, symbole m3 ; pluriel : mètres cubes ;
  • mètre par seconde au carré, symbole m/s2 ;
  • seconde à la puissance moins un, symbole s−1.

Aucune adjonction au symbole d'une unité pour donner une information concernant la nature particulière de la grandeur ou le contexte de mesurage considéré n'est permise : Ueff = 500 V et non U = 500 Veff (« tension efficace exprimée en volts » et non « volts efficaces »). De même, l'appellation « mètre linéaire » ne doit pas être employée, l'adjectif « linéaire » n'apportant aucune notion supplémentaire à l'unité.

Pour former les noms des unités multiples et sous-multiples, des préfixes du Système international sont simplement accolés (sans espace ni tiret) à gauche de l'unité, toujours sans mélanger les symboles (entités mathématiques) et les noms des unités et préfixes : kilomètre (ou km), milliseconde (ou ms). On ne peut pas accoler plusieurs préfixes à une unité (nanomètre mais pas millimicromètre). Ainsi, même si le décanewton (daN) est une unité correcte (qui traduit approximativement l'ancien kilogramme-force), le kilodécanewton (kdaN, qui traduirait la tonne-force) ne l'est pas. De même, un hectopascal (hPa) est un multiple correct de l'unité dérivée, le pascal, mais le kilohectopascal (khPa, qui correspond sensiblement à une pression d'une atmosphère) ne l'est pas.

Note : dans le cas du kilogramme, unité de base qui pour des raisons historiques comporte dans son nom le préfixe « kilo », les multiples et sous-multiples restent formés sur le gramme.

Histoire et évolutions

Avant la Révolution française : premières ébauches d'un système d'unités universel
Frontispice de An Essay Towards A Real Character and a Philosophical Language.

La première tentative notable d'établir des unités universelles (c'est-à-dire fondées sur des phénomènes physiques reproductibles) est, dans le monde anglo-saxon, celle de John Wilkins, un scientifique anglais membre de la Royal Society, qui définit en 1668 une longueur puis un volume universel et enfin une masse universelle (celle de la quantité d'eau de pluie contenue dans un cube de côté valant la longueur universelle). La longueur universelle ainsi définie est prise comme valant 38 pouces de Prusse (approximativement 993,7 mm) soit environ celle d'un pendule simple dont la demi-période des petites oscillations est d'une seconde[17].

Vers 1670 Gabriel Mouton, religieux lyonnais, propose une unité de longueur en se basant sur la mesure d'un arc de méridien terrestre. Il définit aussi la série de multiples et sous-multiples d'unité basée sur le système décimal[18].

En 1675, le savant italien Tito Livio Burattini renomme la mesure universelle de John Wilkins en « mètre » (metro cattolico) et en prend pour définition exacte celle du pendule précédemment décrit (et non plus celle de 38 pouces de Prusse), aboutissant ainsi à une longueur de 993,9 mm[19]. Cette valeur dépend cependant de l'accélération de la pesanteur et varie donc légèrement d'un lieu à l'autre.

Révolution française et naissance du système métrique

En 1790, l’Assemblée nationale constituante se prononce, sur proposition de Talleyrand, lui-même conseillé par Condorcet, pour la création d'un système de mesure stable, uniforme et simple, et c'est l'unité de Burattini qui est d'abord adoptée comme unité de base. Mais du fait que la longueur du pendule battant la seconde n’est pas la même selon l’endroit où l'on se trouve, en raison de la différence de gravité selon la distance avec l'équateur (voir supra), c’est finalement une mesure fondée sur la mesure du méridien de la Terre qui est choisie en 1793[20]. Cette longueur sera précisée, par la loi du 18 germinal an III (), comme étant « la mesure de longueur égale à la dix-millionième partie de l'arc de méridien compris entre le pôle boréal et l'équateur »[21]. Deux savants sont chargés d'effectuer les mesures géodésiques nécessaires, Delambre et Méchain, lesquels vont, durant sept ans, mesurer la distance entre Dunkerque et Barcelone[22].

Mètre étalon réalisé par Chalgrin en 1797 et fixé sur la façade du 36 rue de Vaugirard, à Paris.

Avec le mètre sont définies les unités de surface et de volume, l'unité de masse (le gramme) et l'unité monétaire (le franc germinal) : on crée ainsi le système métrique décimal[21], permettant de convertir plus aisément les unités puisque, désormais, pour passer d'une unité à ses multiples et sous-multiples, il suffit de déplacer la virgule. Dans le même décret, la Convention nationale prévoit la création d'étalons pour le mètre[23]. La définition ainsi choisie est définitivement adoptée le 18 germinal an III () par décret de la Convention nationale française[24],[21]. Ce système métrique est alors désigné[Par qui ?] par le sigle MKpS, pour « mètre, kilogramme-poids, seconde ».

Les étalons du mètre et du kilogramme, en platine, prévus par les décrets de la Convention nationale sont déposés aux Archives nationales de France le 4 messidor an VII (), ce qui est parfois considéré comme l’acte fondateur du système métrique[25].

Introduit par le décret du 1er vendémiaire an IV ()[26], le système métrique est rendu obligatoire en France à l’occasion de son cinquième anniversaire par l'arrêté du 13 brumaire an IX (), l'emploi de tout autre système étant interdit. Dans ses mémoires de Sainte-Hélène, Napoléon, qui avait naguère soutenu l'expédition géodésique en vue de déterminer la nouvelle mesure, mais pris conscience de la difficulté d'acclimatation à de nouvelles unités, écrit :

« Le besoin de l'uniformité des poids et mesures a été senti dans tous les siècles ; plusieurs fois les états généraux l'ont signalé […] La loi en cette matière était si simple, qu'elle pouvait être rédigée dans vingt-quatre heures […] Il fallait rendre commune dans toutes les provinces l'unité des poids et mesures de la ville de Paris […] Les géomètres, les algébristes, furent consultés dans une question qui n'était que du ressort de l'administration. Ils pensèrent que l'unité des poids et mesures devait être déduite d'un ordre naturel, afin qu'elle fût adoptée par toutes les nations […] Dès ce moment on décréta une nouvelle unité de poids et mesures qui ne cadra ni avec les règlements de l'administration publique, ni avec les tables de dimensions de tous les arts […] Il n'y avait pas d'avantage à ce que ce système s'étendît à tout l'univers ; cela était d'ailleurs impossible : l'esprit national des Anglais et des Allemands s'y fût opposé […] Cependant on sacrifiait à des abstractions et à de vaines espérances le bien des générations présentes […] Les savants conçurent une autre idée tout à fait étrangère au bienfait de l'unité de poids et de mesures ; ils y adaptèrent la numération décimale […] ils supprimèrent tous les nombres complexes. Rien n'est plus contraire à l'organisation de l'esprit, de la mémoire et de l'imagination […] Enfin, ils se servirent de racines grecques, ce qui augmenta les difficultés ; ces dénominations, qui pouvaient être utiles pour les savants, n'étaient pas bonnes pour le peuple […] C'est tourmenter le peuple pour des vétilles[27] !!! »

Estampe de 1800 montrant l’usage de six nouvelles unités de mesure et leur équivalence avec les mesures anciennes.

Évolutions du système métrique au XIXe siècle

Dès 1801, la République helvétique tente d'introduire le système métrique, « mais la loi ne fut jamais appliquée » — il fallut attendre 1877. C'est le Royaume uni des Pays-Bas (comprenant les actuels Pays-Bas, la Belgique et une partie du Luxembourg) qui l'adopte à nouveau le premier en 1816, sur l'impulsion de son souverain Guillaume Ier des Pays-Bas, quatorze ans avant la révolution française de 1830, qui signe sa réintroduction en France[28].

Le , Napoléon prend un décret impérial instaurant pour le commerce de nouvelles unités au nom conforme à l'usage ancien, comme aune, toise, boisseau, livre, mais avec de nouvelles valeurs fixées en référence au système métrique, et surtout, autorise pour ces nouvelles unités des fractions non décimales[29].

Après la Restauration française en 1814, Louis XVIII confirme dans un premier temps vouloir poursuivre l'établissement du système métrique, mais sous la pression des plaintes, un arrêté ministériel du ordonne la suppression des fractions décimales des poids et mesures, et l'emploi exclusif des mesures « usuelles » pour la vente au détail des denrées et marchandises.

Le système métrique n'est néanmoins pas abandonné dans l'enseignement et la recherche[30], et petit à petit, on prend conscience qu'il est temps de renoncer aux facilités introduites par le décret de 1812 et de s'en tenir aux unités légales établies par l'arrêté du 13 brumaire an IX. Ce sera l'objet de la loi du [31] signée par Louis-Philippe, qui rend obligatoire l'usage des unités du système métrique à partir du , dans le commerce et dans la vie civile et juridique.

En 1832, Gauss travaille pour l'application du système métrique comme système d'unités cohérent en sciences physiques. Il établit des mesures absolues du champ magnétique terrestre en utilisant un système d'unités fondé sur les unités centimètre, gramme et seconde parfois appelé « Système de Gauss »[25].

Dans les années 1860, Maxwell et Kelvin s’impliquent au sein de la British Association for the Advancement of Science (BA), fondée en 1831, pour la mise en place d'un système d'unités composé d'unités de base et d'unités dérivées. Ceci aboutit en 1874 à la création du « système CGS » fondé sur les unités centimètre, gramme et seconde[25].

Dans les années 1880, la BA et le Congrès international d’électricité, ancêtre de la Commission électrotechnique internationale, s’accordent sur un système d'unités pratiques, parmi lesquelles l’ohm, le volt et l’ampère[25].

Depuis la fondation de la Convention du Mètre

En 1875, la Convention du Mètre est créée et instaure le Bureau international des poids et mesures (BIPM), le Comité international des poids et mesures (CIPM) et la Conférence générale des poids et mesures (CGPM)[32]. La première CGPM a lieu en 1889 et adopte de nouveaux prototypes pour le mètre et le kilogramme[33]. Le système d'unités consacré est alors le « système MKS », du nom de ses unités de base, le mètre, le kilogramme et la seconde.

En 1901, le physicien Giovanni Giorgi montre qu'il est possible de combiner les unités électriques à celles du système MKS en ajoutant, à ce dernier, une unité électrique. La discussion de cette proposition par des organisations internationales parmi lesquelles l'Union internationale de physique pure et appliquée (IUPPA) et la Commission électrotechnique internationale aboutit en 1946 à l'adoption par le CIPM du « système MKSA », fondé sur le mètre, le kilogramme, la seconde et l'ampère[25]. En 1954, après une enquête du BIPM ayant commencé en 1948, la CGPM entérine l'adoption des unités de base supplémentaires que sont le kelvin et la candela[34].

Il reste alors peu d'étapes avant l'achèvement du système métrique actuel. Tout d'abord, lui donner son nom (« Système international d'unités », avec comme abréviation internationale « SI ») ; ce qui est fait en 1960[35]. Ensuite, lui adjoindre comme dernière unité la mole, ce qui est fait en 1971[36].

Redéfinition de 2018-2019

Les unités de base du Système international sont redéfinies lors de la conférence générale des poids et mesures du 13 au (à Versailles), à partir de sept constantes physiques[37] dont la valeur exacte est alors « définitivement fixée »[38]. Cette réforme entre en vigueur le [39].

Utilisation dans le monde
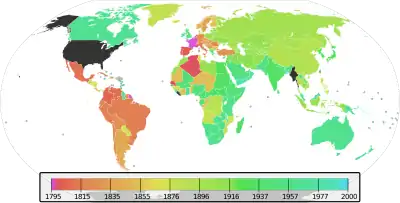
Carte montrant l'année d'adoption du Système international, de la plus ancienne, en rouge, à la plus récente, en vert. Les pays en noir ne l'ont pas encore officiellement adopté.

La plupart des pays du monde ont fait du Système international leur système officiel d'unités. En Asie de l'Est, ce fut au début du XXe siècle[40]. Durant les années 1970, le gouvernement du Canada procède à la conversion au système métrique, sous l'égide de la Commission du système métrique. Cette action (passer officiellement d'un système d'unités national au système métrique) s'appelle métrification.

En 2008, seuls trois pays dans le monde n'ont pas officiellement adopté le Système international : les États-Unis, le Liberia et la Birmanie[41].

Il convient de nuancer en ce qui concerne les États-Unis, signataire de la Convention du Mètre :

  • l'usage du SI y est licite depuis 1866[42] ;
  • métrologiquement parlant, depuis 1895 et le Mendenhall Order (en), le SI est le système de référence (les grandeurs du système impérial sont définies par rapport aux étalons primaires du système métrique) ;
  • le SI est le système recommandé par le Metric Conversion Act (en) de 1975 ;
  • confirmé en 1988 par le Omnibus Foreign Trade and Competitiveness Act (en) ;
  • le SI est de plus en plus répandu parmi les scientifiques, la médecine, le gouvernement, et plusieurs secteurs de l'industrie[41].

Par pays
La sonde Mars Climate Orbiter, perdue en raison d'une confusion de systèmes d'unités.

En France, il existe quelques exceptions notables, utilisant les unités impériales, des unités dérivées du SI, ou d’anciennes unités d’origine plus obscure :

  • en plomberie, les dimensions sont données généralement en fractions de pouce ;
  • la diagonale d'affichage des écrans électroniques (d'ordinateurs, téléviseurs, de mobiles, etc.) s'exprime en centimètres, mais les commerçants lui préfèrent souvent l'usage du pouce[43] ;
  • les pointures de chaussures dont le calcul est dérivé du SI par une formule dont il est difficile de déterminer l'origine[44] ;
  • la température, en dehors du milieu scientifique, est souvent exprimée en degrés Celsius ;
  • en diététique, la valeur énergétique des aliments s'exprime le plus souvent en Calories ;
  • les vitesses courantes (telles que celles des véhicules) sont quasi systématiquement exprimées en km/h et non pas en m/s ;
  • les consommations électriques sont exprimées en kWh et non en MJ.

Au Royaume-Uni, l'usage du système métrique est légalisé depuis 1897[45],[46] mais dans certains domaines tels que le commerce[alpha 5], la santé publique, la sécurité, l'administration, la signalisation routière et la vente de métaux précieux[47], l'équivalent en unités impériales est toléré.

Aux États-Unis, il est possible de trouver dans la même documentation des données métriques et impériales. Cette utilisation conjointe de deux types d'unités de mesure est à l'origine de la perte de la sonde spatiale Mars Climate Orbiter en .


Au Canada, y compris au Québec, l'usage du système métrique est obligatoire depuis 1975, mais dans la plupart des domaines de la vie quotidienne, du commerce, de la construction, c'est le système impérial qui prédomine (surtout en dehors du Québec). Il est commun que des individus ignorent comment utiliser le système métrique dans le domaine des distances (en dehors du code de la route, où il est appliqué systématiquement) : nombreux sont ceux qui ignorent leur taille en mètres (pieds, pouces) et leur poids en kilogrammes (livres) ; de même il est commun de mesurer les dimensions d'un appartement (pieds-carrés), la largeur d'un terrain (pieds), la diagonale d'affichage des écrans électroniques (ordinateurs, TV, mobiles, etc.), ou en plomberie, en système impérial.

La plupart des unités de mesures non métriques sont maintenant définies à partir des unités du Système international. Par exemple, le National Institute of Standards and Technology édite une table des définitions des unités de mesure anglo-saxonnes à partir des unités métriques[48].

Par domaine

Dans la navigation maritime, on compte les distances en milles marins (« milles » ou « milles nautiques », parfois improprement « nautiques » ; en anglais : « nautical miles », abréviation NM ou M), un mille valant 1 852 mètres. La vitesse est exprimée en nœuds marins, un nœud valant un mille marin par heure.

Dans la navigation aérienne, on compte les distances et les vitesses de la même façon que sur un navire : les distances en milles marins et les vitesses en nœuds (« knots » en anglais, langue internationale de l'aéronautique). Les anémomètres, instruments du tableau de bord des avions qui mesurent la vitesse par rapport à l'air, s'ils ne sont gradués que d'une seule grandeur, le sont en « knots » ; s'ils sont gradués de deux grandeurs, ils sont gradués concentriquement en « knots » et en km/h, dont le rapport est de 1/1,852. L'altitude est exprimée en pieds anglais (un pied valant 0,304 8 m). Opérationnellement, on compte en milliers de pieds, et plus exactement encore on parle de « niveau de vol » (FL, « flight level »), exprimé en centaines de pieds. Par exemple, une altitude de croisière de niveau 350 vaut 35 000 pieds, soit 10 668 m. De même, les circuits d'attente au-dessus des aéroports sont espacés verticalement de 10 FL. La vitesse verticale d'un avion de ligne, quant à elle, est indiquée par un variomètre, gradué le plus souvent en milliers de pieds par minute.

Notes et références

Notes
  1. Le système métrique fut introduit en 1793 avec huit préfixes (deux n'ont pas été conservés). La date inscrite dans la colonne est celle à laquelle l'unité a été reconnue par une résolution de la Conférence générale des poids et mesures.
  2. L'échelle longue utilisée ici est la référence dans les pays francophones, notamment en France, au Canada, ainsi que généralement en Europe (sauf en Grande-Bretagne). L'échelle courte est utilisée avant tout par les États-Unis d'Amérique, le Brésil, la Grande-Bretagne et les autres pays de langue anglaise (sauf le Canada).
  3. La reconnaissance en 1948 du micron par la CGPM a été abrogée en 1967. Les anglophones utilisent souvent le u minuscule au lieu du µ, par exemple dans les schémas électroniques (où l'on trouve uF et uH au lieu de µF et µH pour microfarad et microhenry), le clavier QWERTY ne comportant pas toujours ce caractère.
  4. Caractère Unicode U+22C5 (opérateur point), saisi avec les combinaisons suivantes :
    - Windows (uniquement sous Word) : 22C5 Alt+C,
    - Windows (sous LibreOffice) : 22C5 Alt+X,
    - Mac OS : ⌥ Alt+22C5,
    - GNU/Linux : AltGr+⇧ Maj+. ou Ctrl+⇧ Maj+U 22C5.
    On utilise parfois à la place le caractère U+00B7 (point médian) :
    - Windows (valable partout) : Alt+0183,
    - Mac OS : ⌥ Alt+⇧ Maj+F ou ⌥ Alt+00B7.
  5. Vente de bière, de cidre et de lait dans des contenants réutilisables.

Références
  1. (en) Bureau international des poids et mesures, The International System of Units (SI) (ISBN 978-92-822-2213-3 et 92-822-2213-6, lire en ligne [PDF]), p. 103-106.
  2. Conférence Générale des Poids et Mesures, Bureau international des poids et mesures.
  3. Liste des normes issues du comité technique responsable des grandeurs et unités.
  4. « Unités SI et recommandations pour l’emploi de leurs multiples et de certaines autres unités », sur Organisation internationale de normalisation, .
  5. Bureau international des poids et mesures 2006, p. 21.
  6. (en) David B. Newell et Eite Tiesinga, The International System of Units (SI), Gaithersburg, (lire en ligne [PDF]), p. 14-16
  7. (en) « Units and Symbols for Electrical and Electronic Engineers - The IET », sur web.archive.org, (consulté le ).
  8. L'anglais trillion est parfois transcrit en « trillion » au lieu d'être traduit en « billion », et de même billion en « billion » au lieu de « milliard ». Quant au symbole « ppb » (part per billion), il signifie bien en français « partie par milliard ».
  9. Bureau international des poids et mesures 2006.
  10. « Grandeurs et unités », Iso.org.
  11. « Principes de l'écriture des nombres, des grandeurs, des unités et des symboles », Boutique.afnor.org.
  12. 9e Conférence Générale des Poids et Mesures, résolution 7, 1948.
  13. Voir également le décret 75-1200 du (JO du ) annexe au décret, notes préliminaires [PDF] : unités de base, formation des multiples et sous-multiples, écriture des nombres, noms des unités, symboles.
  14. 16e Conférence Générale des Poids et Mesures, résolution 6, 1979.
  15. Lexique des règles typographiques en usage à l’Imprimerie nationale, Imprimerie nationale, 2002 ; édition (ISBN 978-2-7433-0482-9), p. 64-65, 179-180.
  16. Bureau international des poids et mesures 2019, p. 35.
  17. (en) John Wilkins, An Essay Towards a Real Character and a Philosophical Language, Part II, chap. VII, 'Of Measure', 1668 [lire en ligne] [PDF].
  18. Chronologie scientifique, technologique et économique de la France p. 91, Danièle et Jean-Claude Clermontel (ISBN 978-2-7483-4682-4).
  19. (it) Tito Livio Burattini, Misura Universale, 1675.
  20. Décret du 9 août 1793 de l'an second de la République lire en ligne sur Gallica.
  21. Décret du 18 Germinal de l'an troisième de la République française lire en ligne sur Gallica
  22. Ken Adler, Mesurer le monde : l'incroyable histoire de l'invention du mètre, Flammarion, 2005.
  23. Unités de mesure – Le Système métrique – Origines, Quid.
  24. Histoire, site du Bureau international des poids et mesures.
  25. Bureau international des poids et mesures 2006, 1.8 – Note historique, p. 19.
  26. Décrets prononcés dans la séance du premier Vendémiaire de la République française une et indivisible, Décret relatif aux poids et mesures lire en ligne sur Gallica
  27. « Mémoires de Napoléon - Campagnes d'Italie » Chapitre XVII (Journée du 18 Fructidor) écrit par Napoléon Bonaparte (1816-1820) Réédité par Tallandier- Thierry Lentz en octobre 2010.
  28. L’introduction du système métrique dans les Pays-Bas méridionaux in Janus, J. Mertens. Revue internationale de l'histoire des sciences et de la médecine, t. 60, p. 1-12, 1973 [résumé en ligne].
  29. Arrêté pour l'exécution du décret impérial du , concernant l'uniformité des poids et mesures, sur bnf.fr.
  30. Isidore Didion Système de notation des diverses unités employées dans les sciences appliquées. – Mémoire de l'Académie nationale de Metz, 1835.
  31. Bulletin des lois de la République française.
  32. Convention du Mètre, 1875 [lire en ligne] [PDF].
  33. 1re Conférence Générale des Poids et Mesures, Résolution 1, 1889.
  34. 10e Conférence Générale des Poids et Mesures, Résolution 6, 1954, sur bipm.org.
  35. 11e Conférence Générale des Poids et Mesures, Résolution 12, 1960.
  36. 14e Conférence Générale des Poids et Mesures, Résolution 3, BIPM, 1971.
  37. Yaroslav Pigenet, « Ces constantes qui donnent la mesure », CNRS Le journal,‎ (lire en ligne, consulté le ).
  38. Christophe Daussy, « Un nouveau système d'unités de mesure pour le XXIe siècle », La Recherche,‎ , p. 60-65 (lire en ligne).
  39. Mathieu Grousson, « Mesures : le grand renversement », sur CNRS, (consulté le ).
  40. Obligatoire au Siam en 1912, au Japon en 1921 et en Chine en 1923, source : A. Alix, « Le système métrique en Extrême-Orient et aux États-Unis », Annales de Géographie, no 167, 1921.
  41. (en) appendix g : weights and measures, CIA.
  42. (en) The Metric Act of 1866 [PDF], sur nist.gov.
  43. Taille des écrans : pouces et cm, sur lememento.fr (consulté le ).
  44. Comment calculer sa pointure de chaussure ?, sur culture-generale.fr (consulté le ).
  45. Jean-Paul Teytaud, Le remplacement des unités de mesure britanniques et américaines par le système international d'unités, Cahiers de l'APLIUT, 1986, 5-3 p. 54-74.
  46. (en) Use of metric weights and measures in trade, sur parliament.uk, 1897.
  47. (en) The Units of Measurement Regulations 1995, Legislation.gov.uk.
  48. (en) Guide for the Use of the International System of Units (SI) / NIST Special Publication 811, National Institute of Standards and Technology / Barry N. Taylor, 1995.

Voir aussi

Bibliographie
  • Bureau international des poids et mesures, Le Système international d'unités, Sèvres, France, BIPM, , 8e éd., 92 p. (ISBN 92-822-2213-6, lire en ligne [PDF]) et le supplément 2014 [PDF], mise à jour de la 8e édition de la Brochure sur le SI (2006)
  • Bureau international des poids et mesures, Le Système international d'unités, Sèvres, France, BIPM, , 9e éd., 109 p. (ISBN 978-92-822-2272-0, lire en ligne [PDF]).
  • Ken Alder (trad. de l'anglais par Martine Devillers-Argouarc'h), Mesurer le monde : 1792-1799, l'incroyable histoire de l'invention du mètre, Paris, Flammarion, coll. « Champs / histoire » (no 776), , 776 p. (ISBN 978-2-08-121311-1).
  • Denis Guedj, Le mètre du monde, Paris, Seuil, , 330 p. (ISBN 978-2-02-040718-2).
  • Henri Moreau, Le Système métrique : des anciennes mesures au système international d'unités, Paris, Chiron, , 119 p. (ISBN 978-2-7027-0236-9).
  • Magdeleine Moureau, Guide pratique pour le système international d'unités (SI), Paris, Technip, , 2e éd., 46 p. (ISBN 978-2-7108-0695-0, lire en ligne).
  • Arkan Simaan et Jean Rosmorduc (avant-propos) (préf. Jean-Claude Pecker), La science au péril de sa vie : les aventuriers de la mesure du monde, Paris, Vuibert, , 204 p. (ISBN 978-2-909680-41-5 et 978-2-711-75347-5).

Filmographie
  • Un mètre pour mesurer le monde, film documentaire d'Axel Engstfeld, Arte, Allemagne, 2010, 55 min [vidéo] (voir Documentaire Arte)

Articles connexes

Liens externes

  • Portail de la physique
  • Portail des technologies
  • Portail de l’Organisation des Nations unies
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.