Topologie différentielle

Les applications de changements de cartes (partie basse de l'illustration) doivent être des difféomorphismes entre ouverts de l'espace euclidien.

Les variétés différentielles constituent le cadre de base de la topologie différentielle. Il s'agit d'« espaces courbes » sur lesquelles il est possible de définir les notions de base du calcul différentiel et intégral. Une variété différentielle se définit d'abord par la donnée d'une variété topologique, espace topologique localement homéomorphe à l'espace ℝⁿ. Les homéomorphismes locaux sont appelés cartes et définissent des systèmes de coordonnées locales. La structure différentielle est définie en exigeant une forme de régularité des applications de transition entre les cartes.

Dès lors il est possible de parler d'application différentiable sur une variété ou entre variétés quand l'expression en cartes locales est différentiable. De façon plus générale un certain nombre de notions et d'objets du calcul différentiel ordinaire « passent au cadre des variétés » dès lors qu'ils vérifient eux-mêmes des relations de transformation convenables vis-à-vis du changement de coordonnées.

Il existe différents modes de définitions possibles des variétés différentielles et l'un des premiers sujets de la topologie différentielle est d'un faire l'étude. On définit ainsi les immersions qui généralisent la notion de courbe ou surface paramétrée, les submersions qui généralisent l'idée de courbe ou surface définie par des équations, les plongements qui ont les meilleures propriétés.

Représentations imparfaites de la bouteille de Klein dans un espace à trois dimensions : elles présentent une auto-intersection dont il faut s'abstraire.

Au commencement et jusqu'au milieu du XIX^e siècle, topologie et géométrie différentielle étaient étudiées du point de vue « de l'extérieur » : les courbes, les surfaces étaient considérées comme des objets complexes situés dans un espace ambiant très simple, un espace euclidien de dimension supérieure. Avec le concept de variété développé à partir de Riemann, le point de vue intrinsèque s'imposa progressivement, avec le constat que certains problèmes se formalisaient de façon naturelle sur des espaces courbes sans que l'idée de déplacement à l'extérieur de cet espace ait un sens clair. Ainsi en est-il par exemple de l'espace-temps en relativité générale.

Par ailleurs le théorème de plongement de Whitney achève de concilier les deux points de vue en montrant que toute variété abstraite définie à l'aide de changements de cartes peut être réalisée comme une sous-variété plongée dans un espace euclidien[1]. Certains plongements ne peuvent être réalisées qu'en exigeant une dimension suffisamment importante : ainsi la bouteille de Klein est-elle une surface très facile à définir à l'aide de cartes, qui peut être plongée dans l'espace ℝ⁴ et seulement immergée dans ℝ³.

Exemple de champ de vecteurs sur une sphère, avec quelques courbes intégrales.

Les premiers objets à considérer sur une variété sont les vecteurs tangents à la variété en un point, qu'il est possible de définir de façon purement intrinsèque. À partir d'eux on définit les notions de covecteur, champ vectoriel, champ tensoriel qui étendent les constructions de l'algèbre multilinéaire au cadre des variétés. Les champs de vecteurs permettent de donner un sens à la résolution d'équations différentielles : on définit le flot du champ X par l'équation ${\displaystyle {\frac {\partial f}{\partial t}}(x,t)=X(f(x,t))}$. Au voisinage d'un point tel que X ne s'annule pas, le théorème du redressement donne une description locale très simple du champ et du flot[2]

En revanche, faute de pouvoir comparer les vecteurs tangents à la variété en un point et ceux en autre point, il n'existe pas de calcul différentiel intrinsèque sur les vecteurs ou les tenseurs ; il y a en fait différentes façons non équivalentes de mener un tel calcul : dérivée de Lie en utilisant un champ de vecteurs comme référence, choix d'une connexion.

C'est ce qui explique que les formes différentielles sont l'objet d'étude le plus riche : même si elles sont de nature tensorielle, elles possèdent un opérateur différentiel naturellement défini, la dérivée extérieure à l'aide de laquelle on introduit la cohomologie de De Rham. En outre les formes différentielles de degré n, à support compact, peuvent être intégrées sur les variétés orientées de dimension n et on bénéficie d'une version étendue du théorème de Stokes. Il est d'ailleurs possible de pousser cette logique plus loin avec la théorie des courants qui donne un sens général à l'idée de dualité formes différentielles-variétés.

La théorie des groupes de Lie est au confluent de plusieurs grandes branches des mathématiques. Il s'agit en effet de groupes dotés d'une structure de variété différentielle, pour laquelle les opérations de groupe — multiplication et inversion — sont différentiables. Ils rendent compte de l'idée de groupe de symétrie à paramétrisation continue, par exemple de la notion très classique de symétrie de rotation en dimension 3. L'espace tangent au groupe de Lie possède une structure naturelle d'algèbre de Lie et l'application exponentielle réalise un difféomorphisme local entre l'algèbre et le groupe. De nombreuses questions peuvent être étudiées autour de la classification des groupes de Lie et de leurs représentations, des espaces homogènes associés. Les considérations algébriques et de topologie différentielle se fécondent mutuellement.

La géométrie différentielle ajoute en général une structure à une variété différentielle, par exemple le choix d'une métrique en géométrie riemannienne, d'une structure complexe ou d'une structure symplectique. Cet enrichissement se traduit également par une exigence plus forte envers la notion d'équivalence ou de déformation de structure. De ce point de vue, les variétés différentiables sont plus « souples » que les variétés munies de structures géométriques additionnelles. La traduction concrète en est la présence chez ces dernières d'invariants spécifiques comme le volume ou la courbure riemannienne, et, partant, une classification plus fine.

Il arrive cependant qu'on utilise une structure de géométrie différentielle comme outil de travail pour établir des résultats de nature topologique, c'est-à-dire indépendants de ce choix de structure. Ainsi en est-il de l'apparition du gradient en théorie de Morse ou du recours à la géométrie riemannienne pour établir la preuve de la conjecture de Poincaré.

La délimitation entre géométrie et topologie différentielle n'est pas toujours évidente, comme en témoigne la position ambigüe de la géométrie (ou topologie) symplectique. Un critère parfois employé est que la géométrie apporte des invariants de nature locale (infinitésimale), alors que la topologie ne se traduit que par des invariants globaux. Une autre caractérisation courante est qu'en géométrie apparaissent des espaces de modules indexés par des paramètres continus, là où la topologie se limite à des paramétrages discrets.

Relations entre les catégories des variétés topologiques, différentielles, différentielles par morceaux et linéaires par morceaux.

En revanche, les variétés différentielles peuvent être vues comme un enrichissement de la structure de variété topologique et sont en un certain sens plus rigides. Certaines variétés topologiques ne possèdent aucune structure différentiable[3]. A contrario, d'autres variétés topologiques peuvent recevoir plusieurs structures différentiables distinctes, i.e. non difféomorphes. C'est le cas des sphères dites « exotiques » ; ce phénomène ne se produit pas en basse dimension, et commence à s'observer sur les sphères à partir de S⁷, la sphère unité de ℝ⁸. Il existe même une infinité non dénombrable de structures non isomorphes sur ℝ⁴ (voir l'article ℝ⁴ exotique (en)).

Certaines constructions en théorie des structures différentiables, par exemple l'existence des fibrés tangents, peuvent être réalisées dans le cadre purement topologique avec quelque effort, pour d'autres c'est impossible.

Il existe également une catégorie intermédiaire entre celles des variétés topologiques et des variétés différentielles : les variétés dites linéaires par morceaux (catégorie PL), puisqu'on demande des applications de transition qui ont cette propriété. On démontre que toute variété différentielle possède une triangulation adéquate pour définir des applications de transition différentiables par morceaux (catégorie PDIFF), et à partir de là qu'on peut la munir d'une structure linéaire par morceaux, qui se révèle en fait unique. Là encore la réciproque est fausse : sur une variété PL on n'a en général ni existence ni unicité d'une structure différentielle[4].

La fenêtre de Viviani illustre une intersection transverse en tout point sauf au point double. Un petit décalage latéral du cylindre la rendrait complètement transverse.

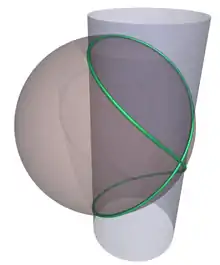
La théorie de la transversalité, initiée par René Thom dans les années 1950, permet de mettre en forme l'idée de position générale dans le contexte des variétés différentielles. Deux sous-variétés sont en effet dites transverses quand, en chaque point d'intersection leurs espaces tangents engendrent l'espace tangent à la variété ambiante. Cette notion peut être opposée à celle de tangence : elle décrit une situation sans intersection, ou des intersections sans tangence. On parle plus généralement d'application ${\displaystyle f:M\to N}$ entre variétés qui est transverse sur une sous-variété W de N en considérant l'image de M. Dans ce cas, l'image réciproque ${\displaystyle f^{-1}(W)}$ est une sous-variété, de même codimension que W[5].

La transversalité possède plusieurs propriétés remarquables. D'une part, il s'agit d'une propriété stable sous de petites perturbations : en termes imagés, si f est une application transverse à W, une application g suffisamment proche de f l'est elle aussi[6]. D'autre part, la transversalité est une propriété générique (en), c'est-à-dire satisfaite par « presque toutes » les applications : ce résultat prend sa source dans le théorème de Sard et le généralise[7]^,[8].

La transversalité peut être déployée pour des familles d'applications, en ajoutant des paramètres (l'ajout de tels paramètres rendant d'ailleurs la transversalité plus facile à atteindre) : on obtient une notion de « transversalité dans une famille » dont l'intérêt est que presque toutes les applications de la famille ont elles-mêmes la propriété de transversalité[9]. On en tire des conséquences directes telles que l'invariance du nombre d'intersection (en) par homotopie[10]. Mais au-delà, de nombreux résultats pertinents sur les champs de vecteurs, applications à valeurs numériques, plongements, etc... peuvent alors être formulés comme des propriétés de transversalité pour lesquelles on récupère les caractères ouvert et générique.

Le parapluie de Whitney, illustre toutes les singularités génériques dans le paramétrage des surfaces de l'espace.

La théorie des singularités se place dans ce contexte : la théorie de la transversalité lui fournit un cadre organisateur qui lui évite de se perdre dans une multitude d'examens de cas spécifiques. Selon la description qu'en donne Vladimir Arnold, elle a pour but de décrire la dépendance des objets étudiés en fonction de paramètres, en se concentrant sur les situations ou une petite variation de ceux-ci engendrent une modification brutale des propriétés de ces objets. De tels phénomènes sont qualifiés de catastrophes et bifurcations. La transversalité peut servir à la fois à établir leur rareté par rapport au cas général et leur nécessité dès lors qu'il y a suffisamment de paramètres, et même à quantifier cela sous forme d'une échelle de fréquence qui n'est autre que la codimension[11].

La théorie de Morse relie la topologie de la variété aux fonctions qui sont définies sur elle. Le principe général est de s'intéresser aux lignes de niveau de ces fonctions, à leur évolution générale et notamment lors du franchissement de valeurs critiques. On s'intéresse aux fonctions dites de Morse, qui ont des points critiques non dégénérés, et qui ont un caractère générique. Des indices des points critiques successifs on peut déduire une décomposition en anses de la variété. On peut aussi opérer cette construction de façon dynamique en suivant les lignes de champ du gradient de la fonction (pour une certaine métrique), et en considérant la façon dont elles relient les points critiques entre eux. On définit ainsi l'homologie de Morse, traduction de l'homologie des variétés compactes, une des premières applications étant les inégalités de Morse sur le nombre minimum de points critiques.

La théorie de Morse peut être étendue au cadre des variétés de dimension infinie, moyennant d'adapter les conditions de compacité ; elle permet ainsi d'établir l'existence de géodésiques fermées sur une variété riemannienne compacte[12]. L'homologie de Floer, dans ses différentes versions, constitue aussi de telles extensions, avec des difficultés techniques considérables, et pas encore toutes élucidées. Un concept central dans ce domaine est celui de courbe pseudoholomorphe et de leur aire (de façon parallèle à l'étude des géodésiques et de leur longueur), qui est reliée directement à la topologie. Ces considérations sont la source d'invariants nouveaux (invariants de Gromov–Witten, de Seiberge-Witten, de Donaldson) et de recherches sur les liens qui les unissent[13].

Un cobordisme entre un cercle (partie supérieure) et une réunion de deux cercles disjoints (partie inférieure).

Deux variétés compactes M et N sont dites cobordantes ou en cobordisme si leur réunion disjointe peut être réalisée comme le bord d'une variété à bord compacte L. Le cobordisme fournit une relation d'équivalence sur les variétés compactes beaucoup plus grossière que les difféomorphismes ou les homéomorphismes mais qui rend plus accessible la classification des variétés[14]. L'ensemble des classes d'équivalence peut être muni d'une structure d'anneau avec pour lois additive la réunion disjointe et multiplicative le produit cartésien. Les classes caractéristiques permettent de définir des invariants pour la relation de cobordisme, appelés nombres caractéristiques[15]. Il existe en outre des définitions du cobordisme plus spécifiques si on veut une compatibilité avec une structure additionnelle, comme un choix d'orientation, une structure spinorielle, ou plus généralement une G-structure (en), des structures de contact, etc.