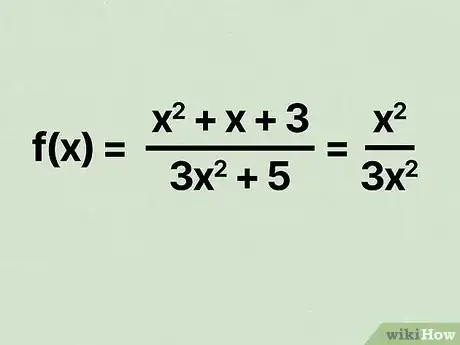This article was co-authored by wikiHow staff writer, Jessica Gibson. Jessica Gibson is a Writer and Editor who's been with wikiHow since 2014. After completing a year of art studies at the Emily Carr University in Vancouver, she graduated from Columbia College with a BA in History. Jessica also completed an MA in History from The University of Oregon in 2013.
This article has been viewed 22,345 times.
Learn more...
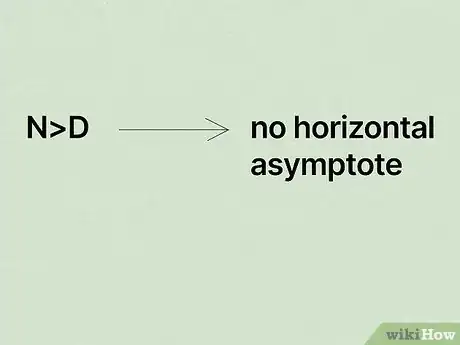
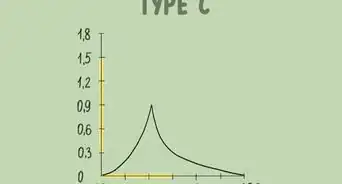
If you see a dashed or dotted horizontal line on a graph, it refers to a horizontal asymptote (HA). In a rational function, an equation with a ratio of 2 polynomials, an asymptote is a line that curves closely toward the HA. The HA helps you see the end behavior of a rational function. In this article, we'll show you how to find the horizontal asymptote and interpret the results of your findings.
Things You Should Know
- A horizontal asymptote is the dashed horizontal line on a graph. The graphed line of the function can approach or even cross the horizontal asymptote.
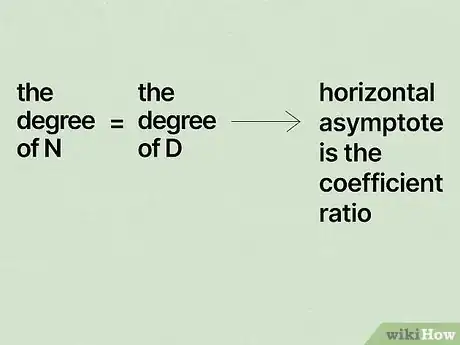
- To find a horizontal asymptote, compare the degrees of the polynomials in the numerator and denominator of the rational function.
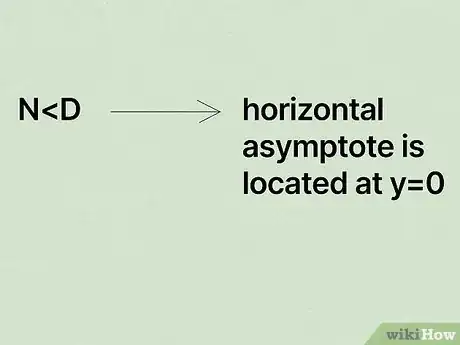
- The degree of difference between the polynomials reveals where the horizontal asymptote sits on a graph.
Steps
How do I find a horizontal asymptote of a rational function?
-
1Remove all terms but the terms with the biggest exponents of . Since you're not actually solving an equation, you're simply comparing the leading terms in your rational function.[2]
- For example, if your equation is , remove all but the leading terms to get .
- As another example, your equation might be . After you remove all but the leading terms, you'll have .
- To give you another example, if you have , ignore the constants to get .
-
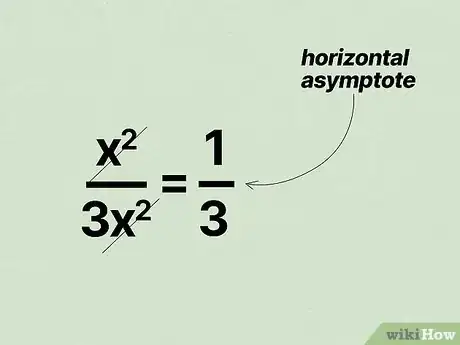
2Simplify the ratio to find the horizontal asymptote for the function. Remember, you're not solving the equation—you're simplifying the leading terms in order to see the limits of the function.[3]
- To go with the previous example of , cancel out both of the to get , which shows you the horizontal asymptote.
- For the other previous example of , cancel out the top and take away from the denominator to get which becomes .
- For the last example of , remove from the numerator and denominator to get .
References
- ↑ https://flexbooks.ck12.org/cbook/ck-12-precalculus-concepts-2.0/section/2.10/primary/lesson/horizontal-asymptotes-pcalc/
- ↑ https://www.math.purdue.edu/academic/files/courses/2016summer/MA15800/Slantsymptotes.pdf
- ↑ https://flexbooks.ck12.org/cbook/ck-12-precalculus-concepts-2.0/section/2.10/primary/lesson/horizontal-asymptotes-pcalc/
- ↑ https://youtu.be/wBZxVxiJS9I?t=289
- ↑ https://sciencetrends.com/how-to-find-horizontal-asymptotes/
- ↑ https://youtu.be/wBZxVxiJS9I?t=222
- ↑ https://www.math.purdue.edu/academic/files/courses/2016summer/MA15800/Slantsymptotes.pdf