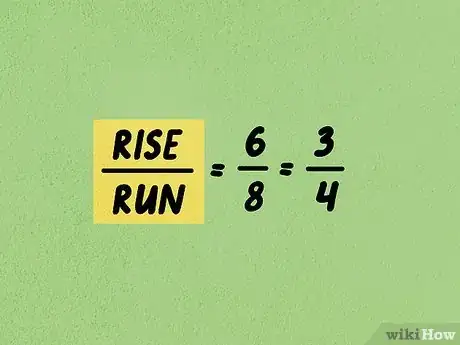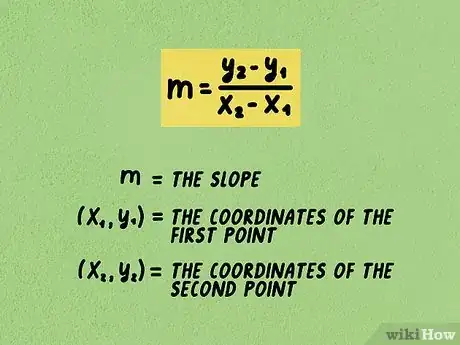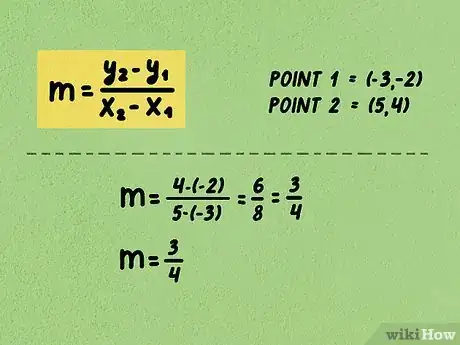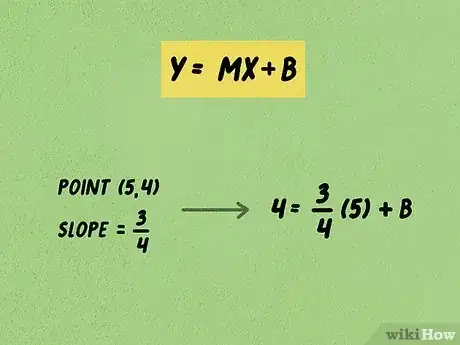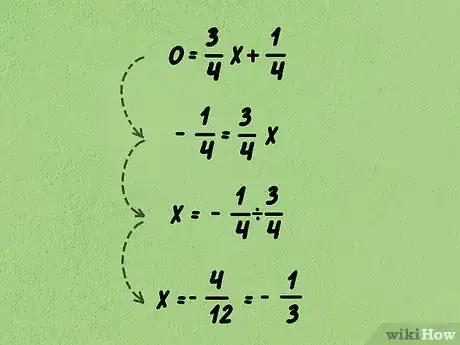Cómo calcular la pendiente y las intersecciones de una línea

La pendiente de una línea mide su nivel de inclinación.^{[1]
X
Fuente de investigación} También puede definirse como la elevación sobre el desplazamiento; es decir, cuánto se eleva la línea en sentido vertical en comparación con su desplazamiento en sentido horizontal. El hecho de poder calcular la pendiente de una línea, o usar la pendiente para encontrar puntos en ella, es una habilidad importante que se utiliza en el campo de la economía^{[2]
X
Fuente de investigación}, las ciencias de la tierra^{[3]
X
Fuente de investigación}, la contabilidad y las finanzas, y muchos otros campos.

Método 1

Método 1 de 4:
Usar un gráfico para hallar la pendiente

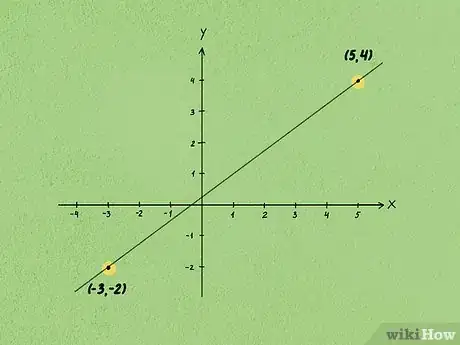
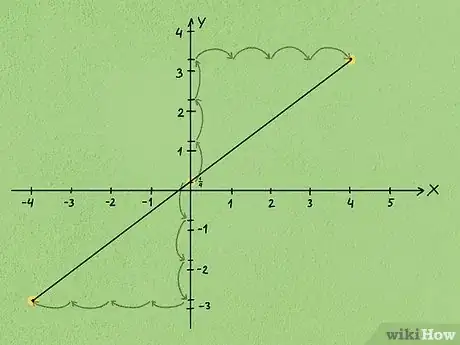
1
Escoge dos puntos de la línea. Dibuja los puntos sobre el gráfico para representarlos y anota sus coordenadas.
- Cuando vayas a graficar puntos, recuerda que primero se mencionará la coordenada $x$ y luego la coordenada $y$ .
- Por ejemplo, podrías elegir los puntos (-3, -2) y (5, 4).
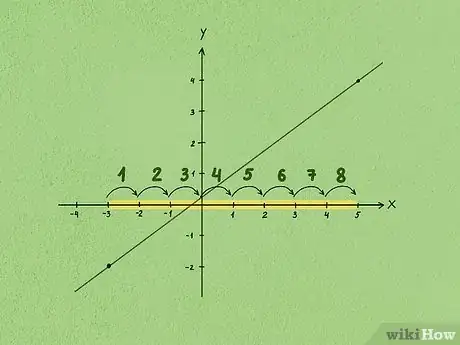
2
Determina cuál es la elevación entre los dos puntos. Para hacerlo, debes comparar la diferencia en “y” de ambos puntos. Comienza por el primer punto, el punto que está más a la izquierda en el gráfico, y cuenta hacia arriba hasta llegar a la coordenada $y$ $y$ del segundo punto.
- La elevación puede ser positiva o negativa. Esto significa que puedes contar hacia arriba o hacia abajo para encontrarla.^{[4]
  X
  Fuente de investigación} Si la línea se mueve hacia arriba y a la derecha, será positiva. Si la línea se mueve hacia abajo y a la derecha, será negativa.^{[5]
  X
  Fuente de investigación}
- Por ejemplo, si la coordenada $y$ del primer punto es (-2) y la coordenada $y$ del segundo punto es (4), contarás 6 puntos hacia arriba. Por lo tanto, la elevación será 6.
3
Determina el desplazamiento entre los dos puntos. Para hacerlo, debes comparar la diferencia en $x$ $x$ de ambos puntos. Comienza por el primer punto, el que está más a la izquierda en el gráfico, y cuenta hasta alcanzar la coordenada $x$ $x$ del segundo punto.
- El desplazamiento siempre será positivo; es decir, solo podrás contar de izquierda a derecha y nunca de derecha a izquierda.^{[6]
  X
  Fuente de investigación}
- Por ejemplo, si la coordenada $x$ del primer punto es (-3) y la coordenada $x$ del segundo punto es (5), contarás hasta 8. Por lo tanto, el desplazamiento será 8.
4
Establece una relación usando la elevación sobre el desplazamiento para determinar la pendiente. La pendiente por lo general se expresa en forma de fracción, pero también puede ser un número entero.
- Por ejemplo, si la elevación es 6 y el desplazamiento es 8, entonces la pendiente sería ${\frac {6}{8}}$ , lo que puede simplificarse a ${\frac {3}{4}}$ .

Método 2

Método 2 de 4:
Usar dos puntos dados para hallar la pendiente

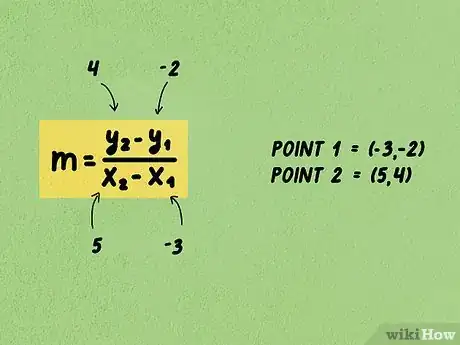
1
Plantea la fórmula $m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . En la fórmula, m = la pendiente, $(x_{1},y_{1})$ $(x_{{1}},y_{{1}})$ = las coordenadas del primer punto, $(x_{2},y_{2})$ $(x_{{2}},y_{{2}})$ = las coordenadas del segundo punto.
- Recuerda que la pendiente equivale a ${\frac {elevacion}{desplazamiento}}$ . Esta fórmula la usarás para encontrar el cambio en $y$ (elevación) sobre el cambio en $x$ (desplazamiento).^{[7]
  X
  Fuente de investigación}
CONSEJO DE ESPECIALISTA

Grace Imson, MA
Instructora de matemáticas en City College de San Francisco
Grace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión de la Universidad de Saint Louis.

Grace Imson, MA
Instructora de matemáticas en City College de San Francisco

Nuestra experta afirma: si tienes la pendiente y un punto, reemplázalos en la ecuación de la línea. En y = mx + b, m es la pendiente, y el punto coordinado tendrá tanto a x como a y. Luego resuelve para hallar b y encontrar la intercepción con el eje y.
2
Reemplaza las coordenadas “x” y “y” en la fórmula. Asegúrate de colocar las coordenadas del primer punto ( $(x_{1},y_{1})$ $(x_{{1}},y_{{1}})$ ) y del segundo punto ( $(x_{2},y_{2})$ $(x_{{2}},y_{{2}})$ ) en la posición correcta en la fórmula. De lo contrario, obtendrás un valor erróneo en la pendiente.
- Por ejemplo, dado que los puntos son (-3, -2) y (5, 4), la fórmula deberá quedar así: $m={\frac {4-(-2)}{5-(-3)}}$ .
3
Completa el cálculo y, si es posible, simplifica la respuesta. Obtendrás como resultado la pendiente, expresada como una fracción o como un número entero.
- Por ejemplo, si la pendiente es $m={\frac {4-(-2)}{5-(-3)}}$ tendrás que calcular $4-(-2)=6$ en el numerador (recuerda que restar un número negativo, equivale a sumar) y $5-(-3)=8$ en el denominador. Puedes simplificar ${\frac {6}{8}}$ a ${\frac {3}{4}}$ , y finalmente $m={\frac {3}{4}}$ .

Método 3

Método 3 de 4:
Hallar la intersección con el eje “y” conociendo la pendiente y un punto de la recta

1
Plantea la fórmula $y=mx+b$ . En la fórmula, $y$ $y$ = la coordenada $y$ $y$ de cualquier punto de la línea; $m$ $m$ = pendiente; $x$ $x$ = la coordenada $x$ $x$ de cualquier punto de la línea; y $b$ $b$ = la intersección con el eje $y$ $y$ .
- $y=mx+b$ es la ecuación de una línea recta. ^{[8]
  X
  Fuente de investigación}
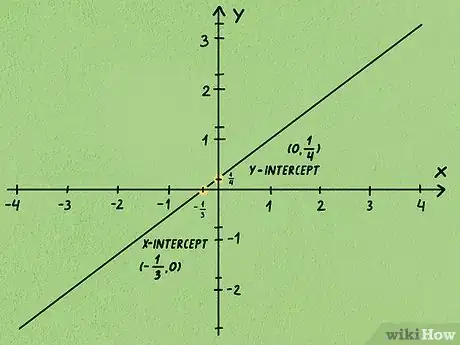
- La intersección con el eje $y$ es el punto a través del cual la línea cruza el eje $y$ .
2
Reemplaza en la fórmula los valores de la pendiente y las coordenadas de un punto de la línea. Recuerda que la pendiente equivale a elevación sobre desplazamiento. Si necesitas encontrar la pendiente, lee las instrucciones que se mencionan anteriormente.
- Por ejemplo, si la pendiente es ${\frac {3}{4}}$ y un punto de la línea es (5,4), entonces la fórmula quedará así: $4={\frac {3}{4}}(5)+b$ .
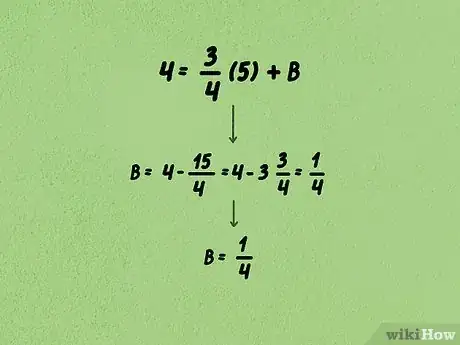
3
Completa la ecuación para hallar el valor de $b$ . En primer lugar, multiplica la pendiente y la coordenada $x$ $x$ . Resta el número en ambos lados para resolver la ecuación y obtener el valor de b.
- En el problema de ejemplo, la ecuación se transformaría en $4=3{\frac {3}{4}}+b$ . Restando $3{\frac {3}{4}}$ en ambos lados, obtendrías ${\frac {1}{4}}=b$ . Por lo tanto, el punto de intersección con el eje y sería ${\frac {1}{4}}$ .
4
Revisa tu trabajo. En un gráfico de coordenadas, dibuja el punto conocido y luego dibuja una línea usando el valor que hayas obtenido para la pendiente. Para encontrar la intersección con el eje $y$ $y$ , observa cuál es el punto donde la línea cruza el eje $y$ $y$ .
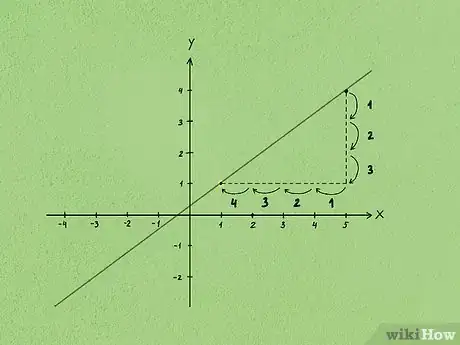
- Por ejemplo, si la pendiente es ${\frac {3}{4}}$ y un punto es (5,4), dibuja un punto en (5,4) y luego otros puntos a lo largo de la línea, contando 3 lugares a la izquierda y 4 hacia abajo. Luego dibuja una línea que atraviese esos puntos. La línea deberá cruzar el eje y justo por encima de la coordenada (0,0).

Método 4

Método 4 de 4:
Encontrar la intersección con el eje x si cuentas con la pendiente y la intersección con el eje y

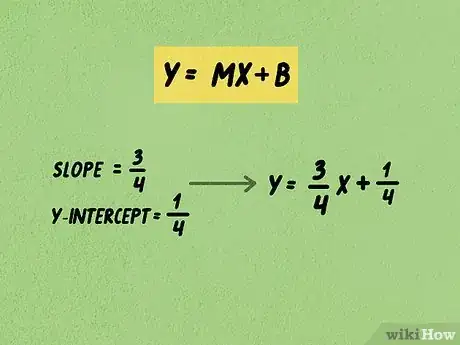
1
Plantea la fórmula $y=mx+b$ . En esta fórmula, $y$ $y$ = la coordenada en $y$ $y$ de cualquier punto de la línea; $m$ $m$ = pendiente; $x$ $x$ = la coordenada en $x$ $x$ de cualquier punto de la línea; y $b$ $b$ = la intersección con el eje $y$ $y$ .
- $y=mx+b$ es la ecuación de una línea recta. ^{[9]
  X
  Fuente de investigación}
- La intersección con el eje x es el punto donde la línea cruza el eje x.
2
Reemplaza en la fórmula los valores de la pendiente y la intersección con el eje y. Recuerda que la pendiente es igual a elevación sobre desplazamiento. Si necesitas encontrar la pendiente, lee las instrucciones que se mencionan anteriormente.
- Por ejemplo, si la pendiente es ${\frac {3}{4}}$ y la intersección con el eje y es ${\frac {1}{4}}$ , la fórmula quedará así: $y={\frac {3}{4}}x+{\frac {1}{4}}$ .
3
Iguala $y$ a 0.^{[10]
X
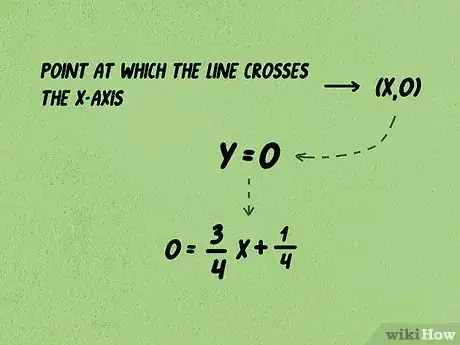
Fuente de investigación} Ahora necesitas encontrar el punto de intersección con el eje x, que es el punto donde la línea cruza el eje x. En ese punto, la coordenada $y$ $y$ equivale a 0. Por lo tanto, si igualas y a 0 y resuelves la ecuación para obtener la coordenada $x$ $x$ , encontrarás el punto ( $x$ $x$ ,0) que es justamente la intersección con el eje $x$ $x$ .
- En el problema de ejemplo, la ecuación se transformaría en $0={\frac {3}{4}}x+{\frac {1}{4}}$ .
4
Completa la ecuación para hallar el valor de $x$ . En primer lugar, resta la intersección con el eje “y” en ambos lados. Luego divide ambos lados entre la pendiente.
- En el problema de ejemplo, la ecuación se transformaría en ${\frac {-1}{4}}={\frac {3}{4}}x$ . Dividiendo ambos lados entre ${\frac {3}{4}}$ , finalmente obtendrías ${\frac {-4}{12}}=x$ . Esto se puede simplificar a ${\frac {-1}{3}}=x$ . Por lo tanto, el punto en el cual la línea cruza el eje x sería $({\frac {-1}{3}},0)$ . La intersección con el eje $x$ sería ${\frac {-1}{3}}$ .
5
Revisa tu trabajo. En un gráfico de coordenadas, dibuja la intersección con el eje $y$ $y$ , luego dibuja una línea usando el valor de la pendiente. Para encontrar la intersección con el eje $x$ $x$ , observa el punto donde la línea cruza el eje $x$ $x$ .
- Por ejemplo, si la pendiente es ${\frac {3}{4}}$ y la intersección con el eje $y$ es $(0,{\frac {1}{4}})$ , dibuja un punto en $(0,{\frac {1}{4}})$ , luego dibuja otros puntos a lo largo de la línea contando 3 lugares hacia la izquierda y 4 hacia abajo, y luego 3 hacia la derecha y 4 hacia arriba. Cuando dibujes una línea a través de los puntos, deberá quedarte una línea que cruce al eje $x$ justo a la izquierda de la coordenada (0,0).
6
Observa el gráfico final.