Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
En matemáticas, algunos problemas te piden reducir una fracción propia (una fracción cuyo denominador es mayor al numerador) a su forma más simple. A veces, puedes perder tiempo tratando de simplificar una fracción que ya no se puede reducir más. Afortunadamente, si empleas algunos trucos, podrás determinar si la fracción está en su forma más simple sin necesidad de hacer ningún cálculo.
Pasos
Parte 1
Parte 1 de 2:Identificar una fracción simplificada
-
1Fíjate si es una fracción unitaria. Una fracción unitaria es aquella que tiene 1 como numerador. Estas no se pueden simplificar más.[1]
- Por ejemplo, , , y son fracciones completamente simplificadas porque tienen 1 como numerador.
-
2Determina si el denominador es un múltiplo del numerador. Una de las maneras de reducir una fracción es dividirla entre el máximo factor común.[2] Si el denominador es múltiplo del numerador, quiere decir que ambos números pueden dividirse entre el máximo factor común (el numerador). Estos tipos de fracciones se pueden reducir para obtener una fracción unitaria.
- Por ejemplo, la fracción no está simplificada, porque 6 es múltiplo de 2. El numerador y el denominador pueden dividirse entre el factor común 2, lo que da como resultado la fracción simplificada .
- La fracción ya está simplificada, porque 5 no es múltiplo de 2.
-
3Determina si el denominador es un número primo. Un número primo es aquel que solo se puede dividir entre 1 y sí mismo.[3] Si el denominador es primo, la fracción ya no se puede reducir más.[4] Esto se debe a que el denominador solo se puede dividir entre sí mismo, por lo que nunca tendrá un factor común con el numerador. Si necesitas más información sobre los números primos, puedes leer este artículo.
- Por ejemplo, la fracción está completamente simplificada, porque 23 es un número primo. Los únicos factores de 23 son 23 y 1, por lo que es imposible encontrar un factor que divida tanto el numerador como el denominador (si el numerador fuese 1, se trataría de una fracción unitaria, que de por sí ya está simplificada, mientras que, si el numerador fuese 23, la fracción sería igual a 1).
-
4Encuentra la diferencia entre el numerador y el denominador. Si la diferencia es 1, entonces la fracción ya está simplificada.
- Por ejemplo, se puede afirmar que la fracción está simplificada, ya que
-
5Reduce las fracciones que todavía no están simplificadas. Para hacerlo, debes hallar el número más grande que pueda dividir el numerador y el denominador para obtener un resultado exacto, y luego hacer la división.[5]
- Por ejemplo, si vas a reducir , tendrás que dividir el numerador y el denominador entre 5. De esta manera, obtendrás , que ya no se puede reducir más porque es una fracción unitaria.
Parte 2
Parte 2 de 2:Usar los trucos según el contexto
-
1Determina cuál de las siguientes fracciones ya está completamente simplificada. No hagas ningún cálculo: , , .
- Las fracciones y ya están en su forma más reducida o simplificada, porque son fracciones unitarias (el numerador es 1). Además, se puede afirmar que no está simplificada, porque 10 es múltiplo de 5.
-
2Evalúa el siguiente problema. Frany dice que es una fracción simplificada. Sin hacer cálculos, ¿cómo puedes probar que esto es correcto?
- Dado que 109 es un número primo, se puede decir que la fracción ya está simplificada. Esto se debe a que 109 solo se puede dividir entre 109 y 1, por lo que no tiene factores comunes con 12.
-
3Determina qué fracción NO está simplificada. No hagas ningún cálculo: , ,
- Ya que , se puede afirmar que la fracción está simplificada. Asimismo, 7 es un número primo; entonces, se sabe que está simplificada. Por último, dado que 8 es un múltiplo de 4, se puede decir que la fracción NO está simplificada.
Consejos
- Recuerda que el numerador es el número que va sobre la barra y el denominador, el que está debajo.
- Estos trucos solo se aplican a fracciones propias.
Referencias
- ↑ http://www.mathwords.com/f/fraction_rules.htm
- ↑ https://www.mathsisfun.com/simplifying-fractions.html
- ↑ http://www.mathsisfun.com/definitions/prime-number.html
- ↑ http://www.webovations.com/education/mathbook/book/numb12b.htm
- ↑ David Jia. Tutor académico. Entrevista a especialista. 7 de enero, 2021.




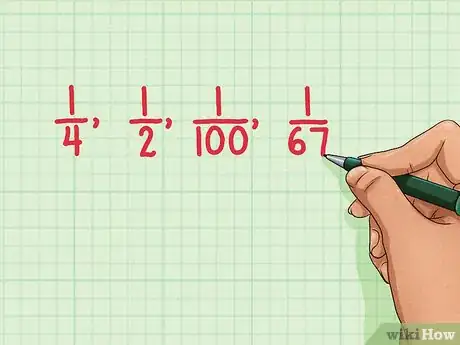




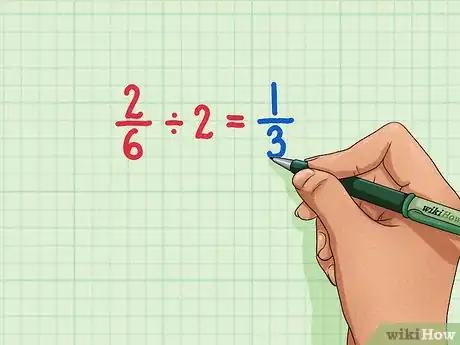








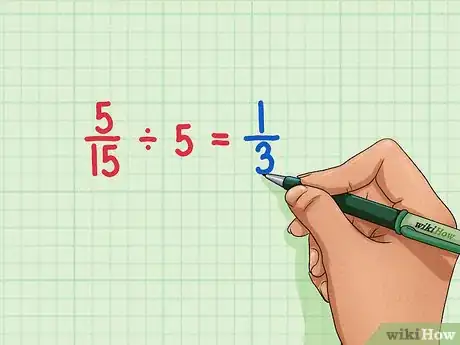




















-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)




