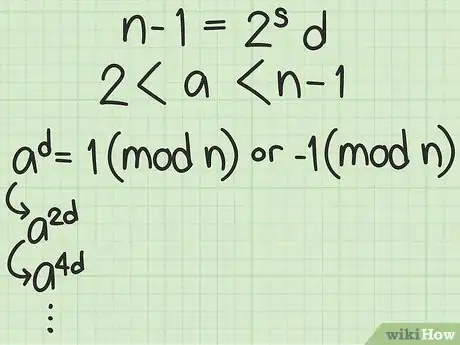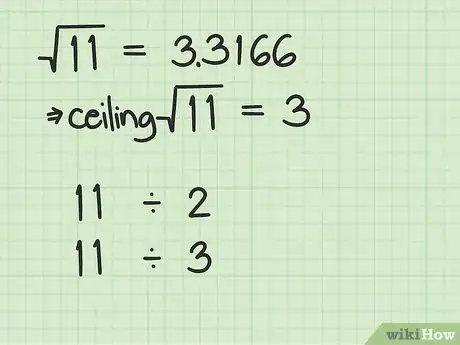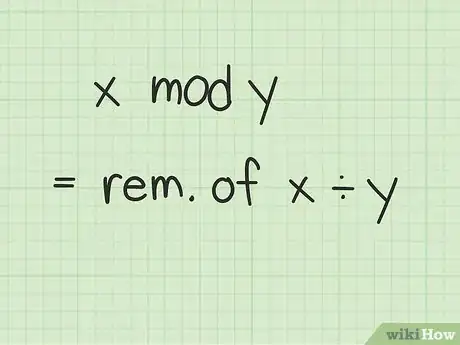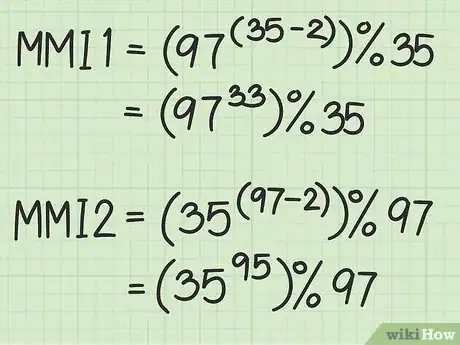Cómo saber si un número es primo

Los números primos son divisibles solo entre sí mismos y 1. Por otro lado, todos los demás reciben el nombre de números compuestos. Existen muchos métodos para saber si un número es primo, pero siempre hay un cierto margen de error. También existen pruebas precisas pero sumamente lentas para analizar números grandes, así como también otras mucho más rápidas, pero que pueden dar resultados falsos. En este artículo, verás algunas opciones para detectar un número primo con base en su tamaño.

Parte 1

Parte 1 de 3:
Utilizar diferentes pruebas para detectar un número primo

Nota: en todas las fórmulas, n es el número cuya primalidad se quiere probar.

1
Utiliza la división por tentativa. Divide n entre cada número primo desde el 2 hasta la función techo ( ${\sqrt {n}}$ ).
2
Realiza el pequeño teorema de Fermat. Advertencia: podrías obtener falsos positivos, incluso para todos los valores de a.
- Asígnale un valor entero a a de modo tal que 2 ≤ a ≤ n - 1.
- Si aⁿ (mod n) = a (mod n), entonces “n” probablemente sea un número primo. Si esto no se cumple, entonces “n” no es primo.
- Haz lo mismo con diferentes valores de a para asegurarte de que sea realmente primo.
3
Realiza el test de primalidad de Miller-Rabin. Advertencia: podrías obtener falsos positivos, pero rara vez ocurre en múltiples valores de a.
- Halla los valores de “s” y “d” de modo tal que $n-1=2^{s}*d$ .
- Asígnale un valor entero a a de modo tal que 2 ≤ a ≤ n - 1.
- Si a^d = +1 (mod n) o -1 (mod n), entonces “n” probablemente sea un número primo. Ahora pasa al resultado de la prueba; de lo contrario, ve al siguiente paso.
- Eleva la respuesta al cuadrado ( $a^{2d}$ ). Si este es igual a +1 (mod n) o -1 (mod n), ve al resultado de la prueba. De lo contrario, repite ( $a^{4d}$ etc.) hasta que $a^{2^{s-1}d}$ .
- Resultado de la prueba: si “n” pasa la prueba, asígnale diferentes valores de a para garantizar su primalidad.
Anuncio

Parte 2

Parte 2 de 3:
Comprender las pruebas para detectar números primos

1
Comprende el método de la división por tentativa. De acuerdo con la definición de primalidad, n solamente es primo si no puede dividirse equitativamente entre números enteros como 2 o mayores. La fórmula dad te ahorra tiempo al descartar las pruebas innecesarias (p.ej.: después de probar 3, no es necesario hacer lo mismo con 9).
- La función techo(x) redondea x al número entero más cercano ≥ x.
2
Comprende la aritmética modular. La operación "x mod y" (abreviatura de “módulo”) significa "dividir “x” entre “y” y hallar el residuo”.^{[1]
X
Fuente de investigación} En otras palabras, en aritmética modular, los números regresan a cero después de alcanzar un determinado valor conocido como el “módulo”. Un reloj cuenta en módulo 12 (es decir, va de 10 a 11 y a 12) y luego vuelve a 1.
- Muchas calculadoras incluyen un botón de “mod”, pero revisa la última parte de esta sección para saber cómo resolverlo a mano para el caso de números grandes.
3
Ten en cuenta los problemas con el pequeño teorema de Fermat. Todos los números que no pasen esta prueba son compuestos (no primos), pero por desgracia, aquellos que sí pasen solo son probablemente primos. Si quieres evitar con toda seguridad los falsos positivos, busca n en una lista de “números de Carmichael” (los cuales pasan esta prueba todo el tiempo) y “pseudoprimos de Fermat” (los cuales pasan esta prueba únicamente para algunos valores de a).^{[2]
X
Fuente de investigación}
4
Utiliza el test de primalidad de Miller-Rabin siempre que corresponda. Si bien es compleja de realizar a mano, esta prueba generalmente se realiza mediante un software. No demora mucho tiempo y tiene pocos falsos positivos en comparación con el método de Fermat.^{[3]
X
Fuente de investigación} Un número compuesto nunca da un falso positivo por más de ¼ de los valores de a.^{[4]
X
Fuente de investigación} Si eliges varios valores de a de manera aleatoria y pasan esta prueba, puedes tener casi toda la seguridad de que n es primo.
5
Realiza la aritmética modular para analizar números grandes. Si no tienes una calculadora con la función “mod” o si la que tienes no puede representar números tan altos, utiliza las propiedades de los exponentes y la aritmética modular para facilitar el proceso.^{[5]
X
Fuente de investigación} En este caso, utilizaremos como ejemplo a $3^{50}$ $3^{{50}}$ mod 50:
- Reescribe la expresión con exponentes más manejables: $(3^{25}*3^{25})$ mod 50 (quizás necesites descomonerlo aún más si vas a realizar el cálculo a mano).
- $(3^{25}*3^{25})$ mod 50 = $(3^{25}$ mod 50 $*3^{25}$ mod 50) mod 50 (esta es una propiedad de la multiplicación modular).
- $3^{25}$ mod 50 = 43.
- $(3^{25}$ mod 50 $*3^{25}$ mod 50) mod 50 = $(43*43)$ mod 50
- $=1849$ mod 50
- $=49$
Anuncio

Parte 3

Parte 3 de 3:
Utilizar el teorema chino del resto

1
Elige dos números. Uno de ellos no debe ser primo, mientras que el otro debe ser el que necesitas analizar para detectar su primalidad.
- “primo1” = 35
- primo2 = 97
2
Elige dos puntos de datos que sean mayores a cero y menores que primo1 y primo2 respectivamente. No pueden ser iguales.
- dato1 = 1
- dato2 = 2
3
Calcula el inverso multiplicativo (IM) de los números primo1 y primo2.
- Calcula el IM:
  - IM1 = primo2 ^ -1 mod primo1
  - IM2 = primo1 ^ -1 mod primo2
- Solo en el caso de los números primos (obtendrás un número para los números compuestos, pero no será su IM):
  - IM1 = (primo2 ^ (primo1-2)) % primo1
  - IM2 = (primo1 ^ (primo2-2)) % primo2
- Por ejemplo:
  - IM1 = (97 ^ 33) % 35
  - IM2 = (35 ^ 95) % 97
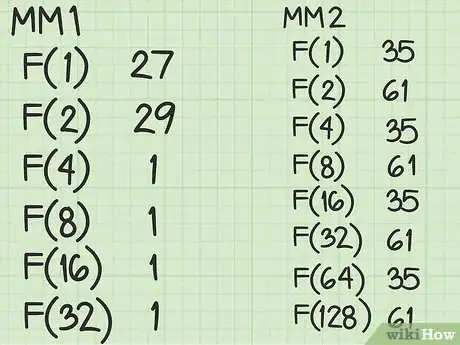
4
Crea una tabla de conversión binaria para cada IM hasta llegar al log2 del módulo.
- Para IM1:
  - F(1) = primo2 % primo1 = 97 % 35 = 27
  - F(2) = F(1) * F(1) % primo1 = 27 * 27 % 35 = 29
  - F(4) = F(2) * F(2) % primo1 = 29 * 29 % 35 = 1
  - F(8) = F(4) * F(4) % primo1 = 1 * 1 % 35 = 1
  - F(16) =F(8) * F(8) % primo1 = 1 * 1 % 35 = 1
  - F(32) =F(16) * F(16) % primo1 = 1 * 1 % 35 = 1
- Realiza la conversión binaria de primo1 - 2
  - 35 -2 = 33 (10001) base 2
  - IMI1 = F(33) = F(32) * F(1) mod 35
  - IM1 = F(33) = 1 * 27 mod 35
  - IM1 = 27
- Para IM2:
  - F(1) = primo1 % primo2 = 35 % 97 = 35
  - F(2) = F(1) * F(1) % primo2 = 35 * 35 mod 97 = 61
  - F(4) = F(2) * F(2) % primo2 = 61 * 61 mod 97 = 35
  - F(8) = F(4) * F(4) % primo2 = 35 * 35 mod 97 = 61
  - F(16) = F(8) * F(8) % primo2 = 61 * 61 mod 97 = 35
  - F(32) = F(16) * F(16) % primo2 = 35 * 35 mod 97 = 61
  - F(64) = F(32) * F(32) % primo2 = 61 * 61 mod 97 = 35
  - F(128) = F(64) * F(64) % primo2 = 35 * 35 mod 97 = 61
- Realiza la conversión binaria de primo2 - 2
  - 97 - 2 = 95 = (1011111) base 2
  - IM2= (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97)
  - IM2= (((((35 * 35) %97) * 61) % 97) * 35 % 97) * 61 % 97) * 35 % 97)
  - IM2= 61
5
Calcula (dato1 * primo2 * IM1 + dato2 * primo1 * IM2) % (primo1 * primo2).
- Respuesta = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35)
- Respuesta = (2619 + 4270) % 3395
- Respuesta = 99
6
Verifica que “primo1” no sea un número primo.
- Calcula (respuesta - dato1) % primo1.
- 99 -1 % 35 = 28.
- Como 28 es mayor que 0, significa que 35 no es un número primo.
7
Verifica si primo2 es un número primo.
- Calcula (respuesta - data2) % primo2
- 99 - 2 % 97 = 0
- Como 0 es igual a 0, significa que 97 probablemente sea un número primo.
8
Repite los pasos del 1 al 7 por lo menos unas dos veces más.
- Si en el paso 7 obtienes un 0:
  - Utiliza un “primo1” diferente, donde primo1 no es un número primo.
  - Utiliza un primo1 diferente, donde primo1 no es un número real. En este caso, los pasos 6 y 7 deben ser iguales a 0.
  - Utiliza diferentes puntos de datos para dato1 y dato2.
- Si el paso 7 siempre da 0 como resultado, existe una probabilidad muy grande de que primo2 sea un número primo.
- En algunos casos, los pasos del 1 al 7 pueden fallar si el primer número no es primo y el segundo es un factor del número compuesto “primo1”. Funciona en todos los casos donde ambos números son primos.
- El motivo por el que se repiten los pasos del 1 al 7 es debido a que hay algunas ocasiones en que, aun cuando primo1 y primo2 sean compuestos, el paso 7 sigue dando como resultado 0, ya sea para uno o para ambos números. No obstante, estas circunstancias son raras. Al convertir primo1 en un número compuesto distinto, si primo2 no es primo, este sin duda será igual a cero en el paso 7. Exceptuando en el caso donde “primo1” es un factor de primo2, los números primos siempre serán iguales a cero en el paso 7.
Anuncio

Consejos

Los 168 números primos menores de 1000 son los siguientes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997 ^{[6]
X
Fuente de investigación}
Si bien el método de división tentativa es más lento que los demás métodos sofisticados específicos para números grandes, sigue siendo muy eficiente para los números pequeños. Incluso para saber si números grandes son primos o no, no es raro que se revise primero los factores pequeños antes de utilizar un método más avanzado en el caso de que no se encuentren dichos factores.

Anuncio