Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 125 480 veces.
Dividir entre un número decimal puede parecer difícil al comienzo. Después de todo, uno nunca aprendió la "tabla del 0,7". El secreto es cambiar el problema de división a un formato que solamente utilice números enteros. Una vez que hayas reescrito el problema de esta manera, se convertirá en un problema de división larga regular.
Pasos
Parte 1
Parte 1 de 2:Escribir el problema como si fuera un problema de división ordinaria
-
1Escribe tu problema de división. Usa un lápiz en caso de que quieras comprobar tus cálculos.
- Ejemplo: ¿Cuánto es 3 ÷ 1,2?
-
2Escribe el número entero como un decimal. Escribe una coma decimal después de toda la cifra y luego escribe ceros después de la coma decimal. Hazlo hasta que los dos números tengan el mismo número de lugares a la derecha de la coma decimal. Esto no cambiará el valor del número entero.
- Ejemplo: en el problema 3 ÷ 1,2, el número entero es 3. Debido a que 1,2 tiene un lugar a la derecha de la coma decimal, tendrás que reescribir 3 como 3,0, de modo que también tenga un lugar después de la coma decimal. Ahora, el problema quedará de la siguiente manera: 3,0 ÷ 1,2.
- Advertencia: no agregues ceros a la izquierda de la coma decimal. El número 3 es igual que 3,0 o 3,00, pero no es igual que 30 o 300.
-
3Mueve las comas decimales hacia la derecha hasta que tengas números enteros. En los problemas de división, está permitido mover las comas decimales, pero solo si las mueves la misma cantidad de lugares para cada número. Esto te permite convertir el problema a números enteros.
- Ejemplo: para convertir 3,0 ÷ 1,2 a números enteros, tendrás que mover las comas decimales un espacio hacia la derecha. De esta manera, 3,0 se convertirá en 30 y 1,2 se convertirá en 12. Ahora, el problema quedará de la siguiente manera: 30 ÷ 12.
-
4Escribe el problema como una división larga. Pon el dividendo (generalmente, el número más grande) debajo del símbolo de la división larga. Escribe el divisor afuera. Ahora tendrás un problema común de división larga que utiliza números enteros. Si quieres recordar cómo hacer una división larga, revisa la siguiente sección.Anuncio
Parte 2
Parte 2 de 2:Resolver el problema de división larga
-
1Calcula el primer dígito de la respuesta. Empieza a resolver el problema tal como lo harías normalmente, comparando el divisor con el primer dígito del dividendo. Calcula el número de veces que el divisor contiene este dígito, y luego, escribe este número encima de ese dígito.
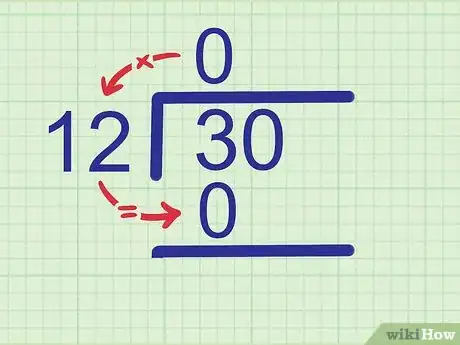
- Ejemplo: quieres dividir 12 entre 30. Compara 12 con el primer dígito del divisor: 3. Debido a que 12 es mayor que 3, entonces estará contenido en este último 0 veces. Escribe 0 encima del 3, en la línea de respuesta.
-
2Multiplica este dígito por el divisor. Escribe el producto (el resultado de la multiplicación) debajo del dividendo. Escríbelo directamente debajo del primer dígito del dividendo, ya que este es el dígito con el que acabas de trabajar.
- Ejemplo: dado que 0 x 12 = 0, escribe 0 debajo del 3.
-
3Resta para encontrar la diferencia. Réstale el producto que acabas de obtener al dígito que está encima. Escribe la respuesta abajo, en una nueva línea.
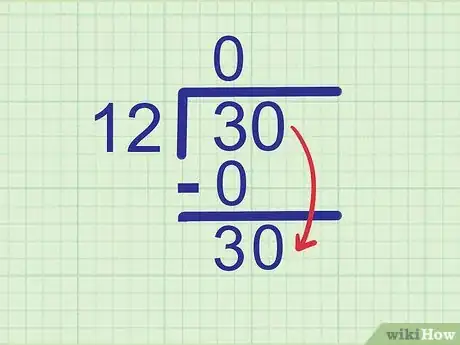
- Ejemplo: 3 - 0 = 3, de manera que tendrás que escribir 3 directamente debajo del 0.
-
4Baja el siguiente dígito. Baja el siguiente dígito del dividendo al lado del número que acabas de escribir.
- Ejemplo: En este caso, el dividendo es 30. Ya trabajamos con en el 3, de modo que el siguiente dígito que debes bajar es 0. Bájalo al lado de tu 3 para formar 30.
-
5Trata de calcular cuántas veces el divisor está contenido en el nuevo número. A continuación, repite el primer paso de esta sección para calcular el segundo dígito de tu respuesta. Esta vez, compara el divisor con el número que acabas de escribir sobre la línea que está más abajo.
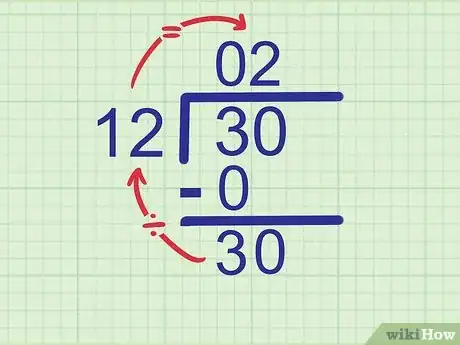
- Ejemplo: ¿Cuántas veces está contenido 12 en 30? El número más cercano es 2, ya que 12 x 2 = 24. Escribe 2 en el segundo espacio de la línea de respuesta.
- Si no estás seguro de la respuesta, haz algunas multiplicaciones hasta que encuentres la respuesta que se aproxime más. Por ejemplo, si te parece que la respuesta es 3, multiplica 12 x 3 y obtendrás 36. Este número es demasiado grande, ya que la idea es calcular cuántas veces está contenido en 30. Intenta con el número menor e inmediato, 12 x 2 = 24. Este si encaja, por lo tanto, 2 es la respuesta correcta.
-
6Repite los pasos anteriores para calcular el siguiente número. Este es el mismo proceso de división larga que acabas de usar y que debe usarse en cualquier problema de división larga:
- Multiplica el nuevo dígito en la línea de respuesta por el divisor: 2 x 12 = 24.
- Escribe el producto en una línea nueva, debajo de tu dividendo: Escribe 24 directamente debajo de 30.
- Réstale la línea de abajo a la que está encima: 30 - 24 = 6; entonces, escribe 6 debajo, en una línea nueva.
-
7Continúa hasta que llegues al final de la línea de respuesta. Si aún falta otro dígito del dividendo, bájalo y resuelve del problema de la misma manera. Si ya llegaste al final de la línea de respuesta, ve al siguiente paso.
- Ejemplo: acabas de escribir 2 al final de la línea de respuesta. Ve al siguiente paso.
-
8Agrega un decimal para extender el dividendo, si fuese necesario. Si la división fue exacta, obtendrás "0" como resultado de la última resta. Esto significa que ya terminaste, y la respuesta de tu problema será un número entero. Pero si ya llegaste al final de la línea de respuesta y todavía queda algo a la izquierda para dividir, tendrás que extender el dividendo agregando una coma decimal seguida de un 0. Recuerda que esto no cambia el valor del número.
- Ejemplo: ya estás al final de la línea de respuesta, pero el resultado de la última resta es "6". Extiende el "30" debajo del símbolo de la división larga añadiendo un ",0" al final. Escribe una coma decimal en el mismo lugar en la línea de respuesta, pero no escribas nada después.
-
9Repite los mismos pasos para hallar el siguiente dígito. La única diferencia aquí es que debes subir la coma decimal hasta el mismo lugar en la línea de respuesta. Una vez que lo hayas hecho, tendrás que hallar los demás dígitos de la respuesta de la misma manera.
- Ejemplo: baja el nuevo 0 hasta la última línea para formar "60." Dado que 12 está contenido en 60 exactamente 5 veces, debes escribir 5 como último dígito en la línea de respuesta. No olvides que debes poner un decimal en la línea de respuesta, de modo que la respuesta final del problema será 2,5.
Anuncio
Consejos
- Si la división larga se prolonga durante mucho tiempo, puedes detenerte en cualquier momento y redondear a un número cercano. Por ejemplo, para resolver 17 ÷ 4,20, simplemente calcula hasta llegar a 4,047 y redondea tu respuesta a "4,05."
- Otra opción es escribirlo como un residuo (de modo que la respuesta de 3 ÷ 1,2 sería "2 con un residuo de 6"). Sin embargo, dado que en este momento trabajas con decimales, es probable que tu profesor espere que también resuelvas la parte decimal de la respuesta.
- Si sigues el método de división larga correctamente, siempre terminarás con la coma decimal en la posición correcta o con ningún decimal en absoluto si la división es exacta. No trates de adivinar dónde poner la coma decimal; a menudo será un lugar distinto al de los números originales con los que empezaste.
- Recuerda los términos de una división:
- El dividendo es el número que vas a dividir.
- El divisor es el número entre el cual vas a dividir otro número.
- El cociente es la respuesta del problema.
- Al juntarlos todos obtienes: Dividendo ÷ Divisor = Cociente.
Advertencia
- Recuerda que 30 ÷ 12 dará exactamente la misma respuesta que 3 ÷ 1,2. No trates de "corregir" la respuesta moviendo los decimales nuevamente.[1]




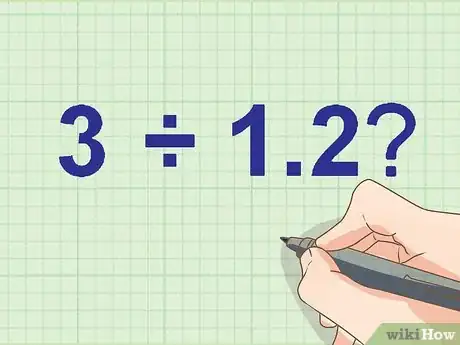




















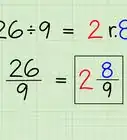
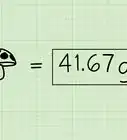


wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 125 480 veces.