Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 11 405 veces.
El sistema conocido de la cuadrícula rectangular es fácil de aprender, pero no es el más conveniente para todas las situaciones (por ejemplo, para trazar los radios de una rueda o el movimiento del agua al irse por el desagüe). Un sistema circular de coordenadas sería más apropiado en estos casos. De hecho, es probable que ya te hayas encontrado en tu vida cotidiana con el concepto básico de las coordenadas polares.[1] Por ejemplo, para determinar de dónde proviene la sirena de un vehículo, debes saber dos cosas: la distancia a la que se encuentra y la dirección de la cual proviene. El sistema de coordenadas polares utiliza este mismo método para trazar puntos, describiendo la distancia de un punto determinado y el ángulo de un rayo fijo.
Pasos
Parte 1
Parte 1 de 4:Trazar coordenadas polares
-
1Dispón el plano polar. Es posible que anteriormente ya hayas usado las coordenadas cartesianas para trazar puntos marcando ubicaciones en una cuadrícula rectangular con la notación . Las coordenadas polares, en cambio, usan un gráfico diferente que está basado en los círculos.[2]
- El punto central del gráfico (también conocido como "origen" en una cuadrícula rectangular) se conoce como el polo y puede etiquetarse usando la letra O.
- Dibuja una línea horizontal hacia la derecha empezando desde el polo. Esta línea constituirá el eje polar. Etiquétala usando unidades de la misma forma como lo harías con el eje x positivo de una cuadrícula rectangular.
- Si tienes papel gráfico polar, podrás observar en él muchos círculos de diferentes tamaños cuyo centro es el polo. Si vas a usar papel en blanco, no tienes que trazar estos círculos tú mismo.
-
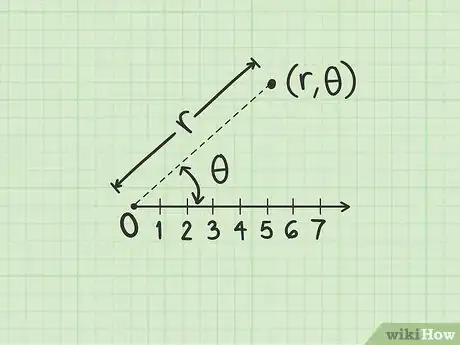
2Comprende las coordenadas polares. En el plano polar, cada punto está representado por una coordenada cuyo formato es :
- La primera variable, , representa el radio. Este punto se encuentra en un círculo cuyo radio es y cuyo centro es el polo (el origen).
- La segunda variable, , representa un ángulo. Este punto se encuentra a lo largo de una línea que atraviesa el polo y forma un ángulo con el eje polar.
-
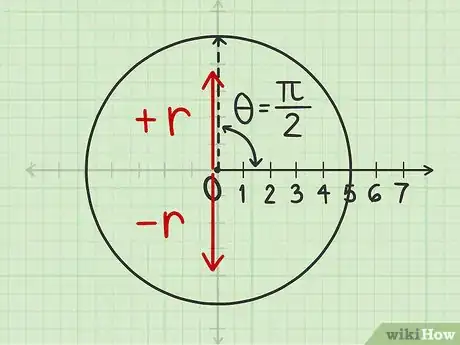
3Repasa la circunferencia goniométrica. En las coordenadas polares, los ángulos suelen medirse en radianes y no en grados sexagesimales. En este sistema, el ángulo de un giro completo (es decir, 360 grados o un círculo completo) mide 2 radianes. (Se establece este valor porque la circunferencia de un círculo con un radio de 1 mide 2). Familiarízate con la circunferencia goniométrica para que te sea mucho más fácil trabajar con las coordenadas polares.
- Por el momento, no te preocupes si tu libro de texto emplea grados sexagesimales, ya que de todas formas es posible trazar puntos polares midiendo en grados sexagesimales.
Anuncio
Parte 2
Parte 2 de 4:Trazar un punto
-
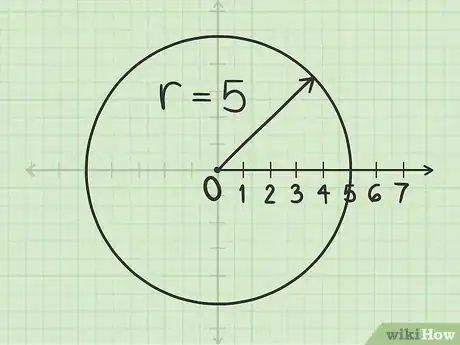
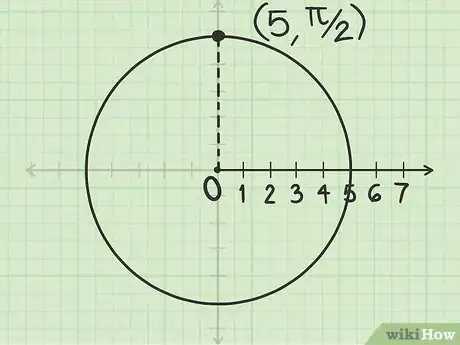
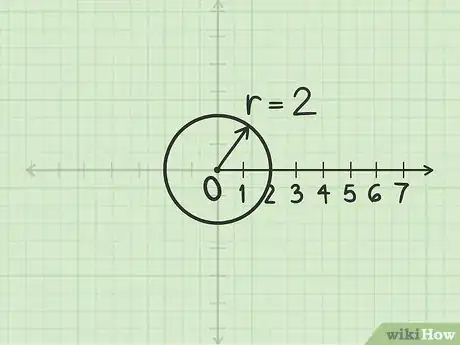
1Dibuja un círculo cuyo radio mida . Las coordenadas polares de cualquier punto tendrán el formato . Para empezar, dibuja un círculo cuyo centro sea el polo y cuyo radio mida .
- El polo es el punto central del gráfico en el mismo lugar en donde se encuentra el origen en un plano rectangular de coordenadas.
- Por ejemplo, si quieres trazar el punto , debes colocar el compás en el polo y extender el extremo en donde se encuentre el lápiz hasta que llegue a las 5 unidades en el eje polar. Luego, haz girar el compás para trazar el círculo.
-
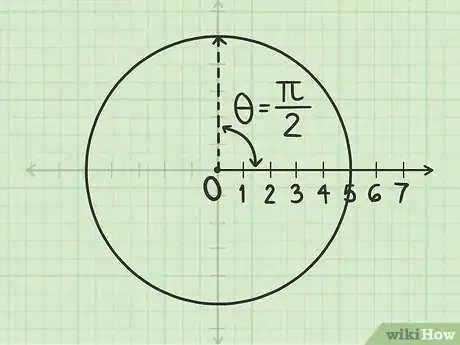
2Mide un ángulo de empezando desde el eje polar. Coloca el transportador de forma que la parte central quede en el polo y el borde se extienda a lo largo del eje polar. Mide el ángulo desde este eje. En caso de que tu transportador solo mida ángulos en grados sexagesimales y el ángulo que debas medir esté en radianes, puedes ya sea convertir las unidades o consultar la circunferencia goniométrica si necesitas ayuda.
- Para el punto , según la circunferencia goniométrica, se encuentra a un cuarto de la circunferencia del círculo, lo que equivaldría a 90 grados desde el eje polar.
- Los ángulos positivos siempre deben medirse en sentido antihorario empezando desde el eje. Los ángulos negativos deben medirse en sentido horario desde el eje.
-
3Traza una línea con base en el signo de . Luego, debes trazar una línea a lo largo del ángulo que hayas medido. Sin embargo, antes de empezar, es importante saber en qué dirección trazarla. Para ello, consulta las coordenadas polares :
- Si es positivo, traza la línea hacia adelante empezando desde el polo y atravesando la marca que hayas hecho en el ángulo.
- Si es negativo, traza la línea hacia atrás empezando desde la marca que hayas hecho en el ángulo, regresando hacia el polo y atravesándolo hasta cruzar el círculo por el lado opuesto.
- No debes confundirte con las coordenadas rectangulares, ya que esto no corresponde a los valores positivos o negativos de un eje x o y.
-
4Etiqueta el punto de intersección de la línea y el círculo. Este punto es .
- El punto se encuentra en un círculo cuyo radio mide 5 y cuyo centro se encuentra en el polo a un cuarto de la circunferencia del círculo en sentido antihorario desde el eje polar. Este punto equivaldría a (0,5) en un plano rectangular.
Anuncio
Parte 3
Parte 3 de 4:Ejemplos
Primer ejemplo
Traza el punto P que se encuentra en las coordenadas en el plano polar.
-
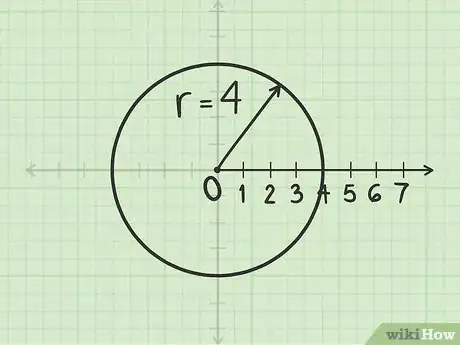
1Traza un círculo cuyo radio mida . Hazlo de forma que el polo sea el centro.
-
2Mide el ángulo radianes. Mide este ángulo empezando desde el eje polar (lo que equivale al eje x positivo). El ángulo es negativo, por lo que debes medirlo en sentido horario.
-
3Traza una línea en este ángulo. Empieza por el polo (el origen). El radio es positivo, por lo que debes desplazarte hacia adelante empezando desde el polo y atravesando el ángulo que hayas medido. El punto en el que la línea y el círculo se cruzan corresponde a .Anuncio
Segundo ejemplo
Traza el punto Q que se encuentra en las coordenadas en el plano polar.
-
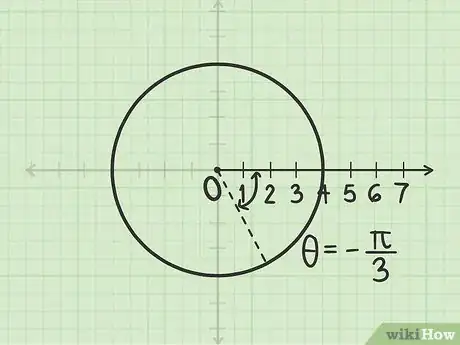
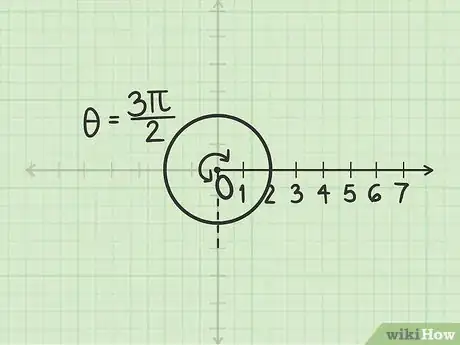
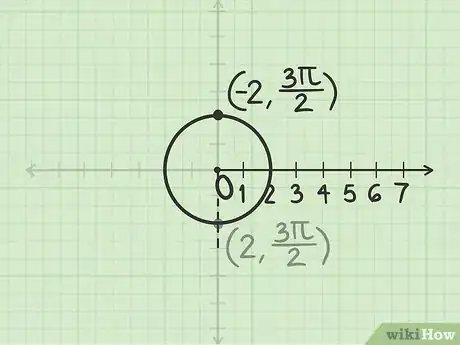
1Traza un círculo cuyo radio mida . Hazlo de forma que el polo sea el centro. El radio en realidad mide -2 pero el signo no es importante en este paso.
-
2Mide el ángulo radianes. El ángulo es positivo, por lo que debes empezar en sentido antihorario desde el eje polar.
-
3Traza una línea en dirección opuesta a este ángulo. El radio es negativo, por lo que debes empezar desde el polo y desplazarte en la dirección opuesta a ese ángulo. La intersección entre la línea y el círculo es el punto .Anuncio
Parte 4
Parte 4 de 4:Convertir coordenadas cartesianas a polares
-
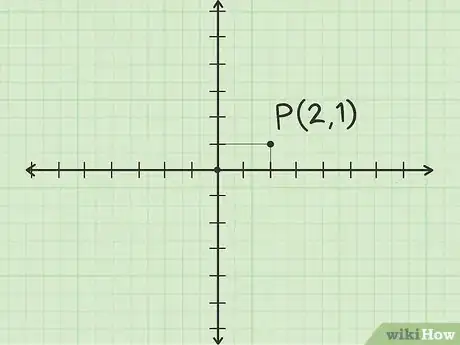
1Considera el punto en el plano cartesiano. Traza una línea de 2 unidades a lo largo del eje x positivo empezando en el origen. Luego, traza una segunda línea empezando desde el punto al que hayas llegado y que mida una unidad en la dirección positiva del eje y. Esto te ubicará en el punto (2,1), el cual debes etiquetar como P.
-
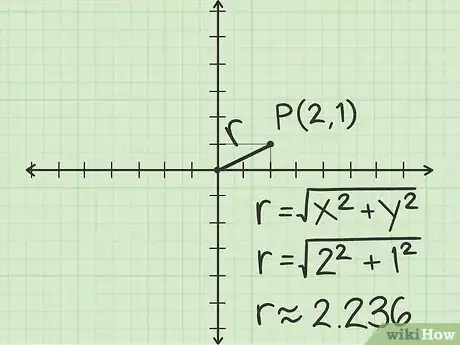
2Encuentra la distancia entre el origen y . Traza una línea entre O y P cuya longitud será en las coordenadas polares y que también constituirá la hipotenusa de un triángulo rectángulo. De esta forma, puedes emplear la geometría para calcular la longitud de la hipotenusa. Por ejemplo:
- Los catetos de este triángulo miden 2 y 1.
- Emplea el teorema de Pitágoras para calcular la longitud de la hipotenusa, la cual será .
- Si quieres encontrar el valor de a partir de coordenadas cartesianas, la fórmula general es , donde es la coordenada de x en el plano cartesiano e es la coordenada de y en el plano cartesiano.
-
3Encuentra el ángulo entre y el eje x positivo. Para encontrar este valor, debes emplear la trigonometría:
-
- La fórmula general para encontrar es , donde es la coordenada de y en el plano cartesiano y es la coordenada de x en el plano cartesiano.
-
-
4Anota las coordenadas polares. Con esto obtendrás los valores de y . Las coordenadas (2,1) en el plano rectangular se convierten en las coordenadas polares aproximadas (2,24, 26,6º) o las coordenadas polares exactas .Anuncio
Consejos
- Memoriza la circunferencia goniométrica y aprende a convertir radianes a grados y viceversa. Esto te será de gran ayuda para trazar coordenadas polares.
- Un punto tiene una cantidad infinita de coordenadas polares, a diferencia de lo que ocurre con el sistema regular de coordenadas. Por ejemplo, el punto (1, 2π) equivale al punto (-1, π) y también a los puntos (1, 4π), (1, 6π), (1, 8π), etc. Cada uno de estos puntos contiene instrucciones para diferentes cantidades de "rotaciones" pero, a la larga, el punto final siempre es el mismo.[3]
Cosas que necesitarás
- papel
- lápiz
- compás
- transportador
















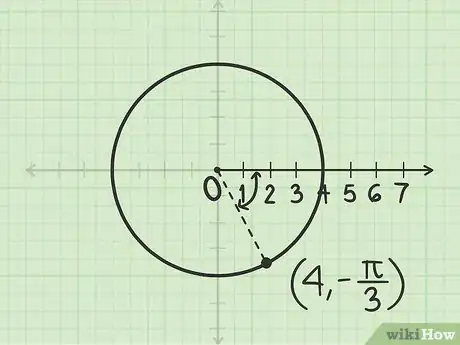










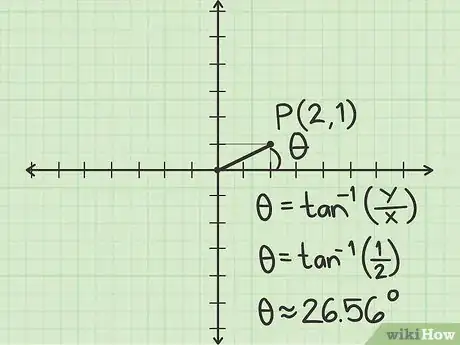




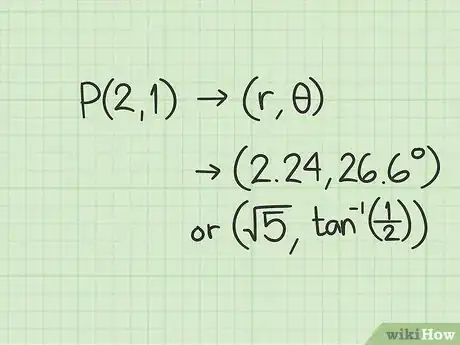




















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 11 405 veces.