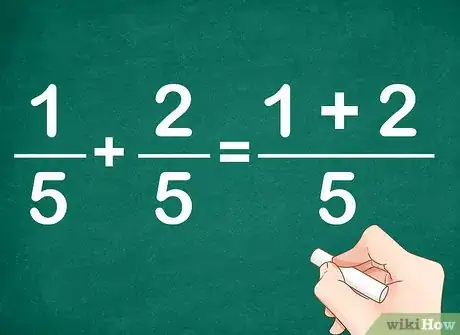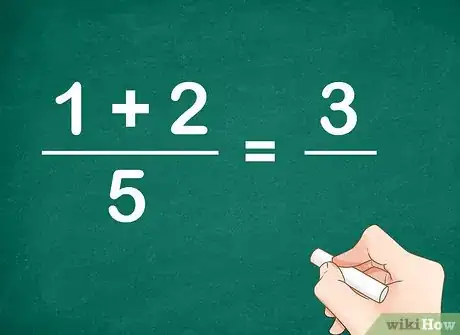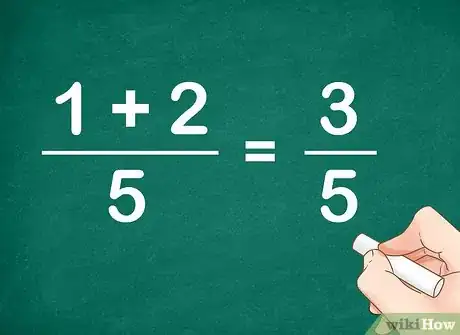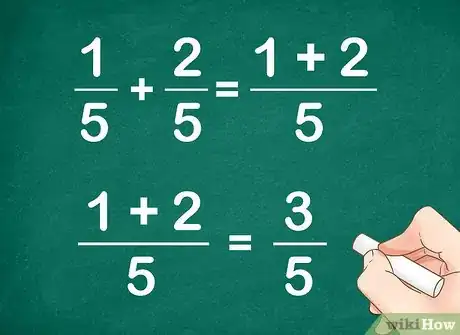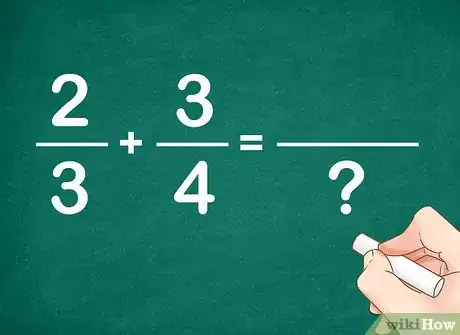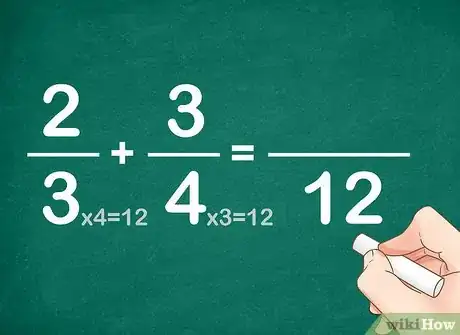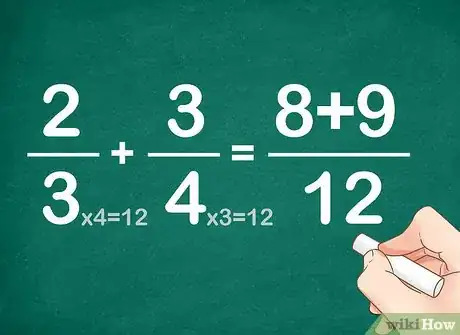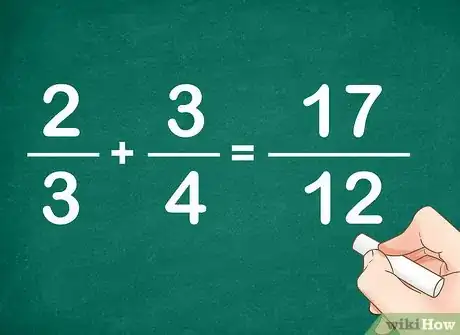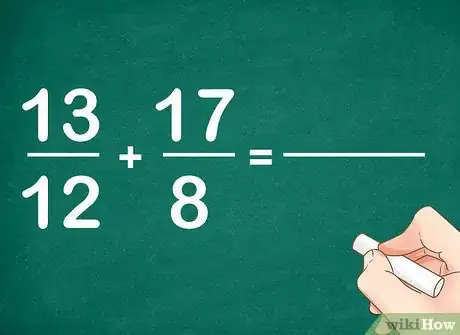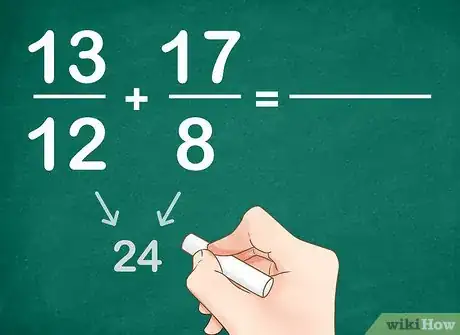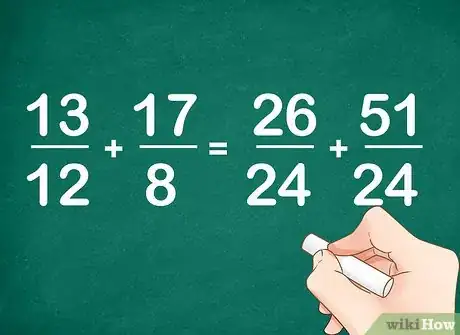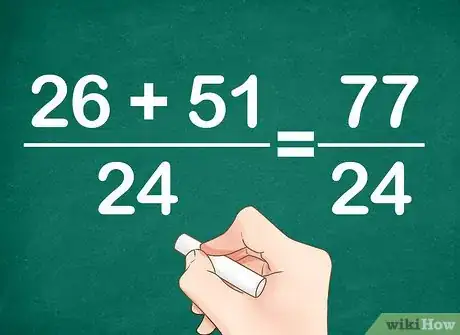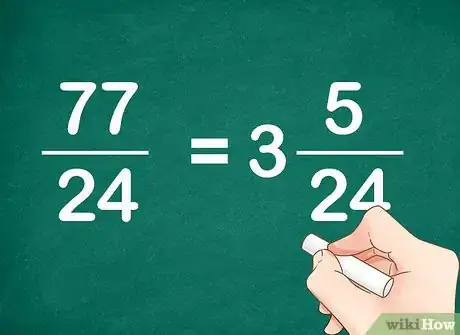wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 10 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 7 884 fois.
Dans certaines situations, il peut être utile de savoir additionner et soustraire des fractions. Ces dernières apparaissent, à des degrés divers, dans tous les programmes de l'école primaire à l'université. Cet article fait le point sur les différents cas de figure dans lesquels il faut additionner ou soustraire des fractions entre elles, que ces fractions soient impropres ou non, qu'elles soient intégrées dans un nombre mixte ou non… Le principe de calcul de toute façon est le même !
Étapes
Méthode 1
Méthode 1 sur 4:Additionner et soustraire des fractions ayant le même dénominateur
-
1Inscrivez votre opération. Si les deux dénominateurs sont identiques, vous pouvez d'ores et déjà placer ce dénominateur sous la barre de fraction de la réponse.
- Autrement dit, si vous devez faire 1/5 + 2/5, vous pouvez écrire directement 1+2/5 = ?. Le dénominateur étant le même, vous ramenez tout au même dénominateur. Les numérateurs sont alors regroupés sur la barre de fraction.
-
2Additionnez les numérateurs. Le "numérateur" est le nombre placé au-dessus de la barre de fraction. Si on reprend notre exemple (1/5 et 2/5), 1 et 2 sont les deux numérateurs.
- Que vous ayez marqué 1/5 + 2/5 ou 1+2/5, votre réponse sera identique : c'est 3, puisque 1 + 2 = 3.
-
3Ne touchez pas au dénominateur ! Dans la mesure où il est le même pour les deux fractions, vous devez le laisser inchangé. Pas d'addition, ni de soustraction, ni de multiplication, ni de division ! Rien !
- Dans notre exemple, le dénominateur est 5. C'est celui des deux fractions, ce sera celui de la réponse !
-
4Donnez votre réponse définitive. Tout ce qu'il vous reste à faire est de mettre le numérateur en haut et le dénominateur en bas ! Pour ce qui est de notre exemple, la réponse définitive est : 3/5.
- Quel est votre numérateur ? Réponse : 3. Votre dénominateur ? Réponse : 5. En conséquence, 1/5 + 2/5 = 1+2/5 = 3/5.
Publicité
Méthode 2
Méthode 2 sur 4:Additionner et soustraire des fractions ayant des dénominateurs distincts
-
1Trouvez le plus petit dénominateur commun aux deux fractions. En fait, il s'agit de trouver le PPCM (Plus Petit Commun Multiple) des dénominateurs, c'est-à-dire le plus petit nombre qui soit à la fois multiple de ces deux dénominateurs. Soit les fractions 2/3 et 3/4. Quels sont les dénominateurs ? Réponse : 3 et 4. Pour trouver le PPCM de 3 et de 4, on peut utiliser une des 3 méthodes suivantes.
- Inscrivez les multiples de chaque dénominateur. Les multiples de 3 sont 3, 6, 9, 12, 15, 18... Les multiples de 4 sont 4, 8, 12, 16, 20… Quel est alors le plus petit commun multiple ? C'est 12 ! Le PPCM est donc 12.
- Faites la décomposition en facteurs premiers. Si vous savez ce qu'est un facteur premier (valeur seulement divisible par 1 et par elle-même), vous pouvez faire la décomposition. En fait, on doit trouver le produit de facteurs premiers qui donne le nombre en question. Ainsi pour 3, la décomposition est la suivante : 3 = 3 x 1 (3 et 1 sont facteurs premiers). Pour 4, la décomposition est la suivante : 4 = 2 x 2 (2 est facteur premier). Multipliez ici tous les facteurs premiers : PPCM = 3 x 1 x 2 x 2 = 12.
- Multipliez les dénominateurs entre eux s'ils sont "petits". Dans certains (et c'est le cas ici), on peut multiplier directement les deux dénominateurs – 3 x 4 = 12. Par contre, cette méthode est à proscrire si les dénominateurs dépassent 10 ! Si vous avez en dénominateur 56 et 44, il faut calculer (2 464) et ça devient alors compliqué.
-
2Multipliez les deux dénominateurs par le nombre adéquat pour obtenir le PPCM. Bref, il faut réduire les deux fractions au même dénominateur – le PPCM. Dans notre exemple, ce dernier est 12, on l'a démontré. Pour la première fraction, il faut multiplier 3 par 4 pour obtenir 12, et pour la seconde fraction, on doit multiplier 4 par 3 pour obtenir le même nombre. Ainsi, les deux fractions ont le même dénominateur.
- Ainsi 2/3 est devenu 2/(3 x 4) et 3/4 est devenu 3/(4 x 3), soit 2/12 et 3/12. Attention ! Ce n'est pas fini !
- Notre exemple est particulier dans la mesure où en fait, on a multiplié les dénominateurs entre eux, mais c'est loin d'être toujours le cas. Parfois, avec de grands dénominateurs, on peut trouver un PPCM inférieur au produit des deux dénominateurs.
- Parfois aussi, il arrive que l'on ait besoin de multiplier qu'un seul des dénominateurs, quand l'un est multiple de l'autre (ex. : pour 1/2 + 3/4, 4 sera le PPCM).
- Ainsi 2/3 est devenu 2/(3 x 4) et 3/4 est devenu 3/(4 x 3), soit 2/12 et 3/12. Attention ! Ce n'est pas fini !
-
3Multipliez aussi les numérateurs par les mêmes nombres. Si l'on multiplie un dénominateur par un nombre, il faut, pour garder la fraction intacte, multiplier également le numérateur par ce même nombre. À l'étape précédente, nous n'en étions donc qu'à la moitié des calculs !
- Nous avions donc 2/(3x4) et 3/(4x3) – maintenant, on équilibre en multipliant les numérateurs par les mêmes quantités. Soit (2 x 4)/(3 x 4) et (3 x 3)/(4 x 3). Calculs faits, cela donne : 8/12 et 9/12. C'est parfait, nos fractions sont inchangées et leurs dénominateurs sont identiques !
-
4Additionnez (ou soustrayez) les numérateurs. La somme 8/12 + 9/12 est facile. On additionne les numérateurs et l'on garde le même dénominateur, en l'occurrence le PPCM.
- Dans notre exemple, on a donc : (8+9)/12 = 17/12. On peut éventuellement transformer cette fraction impropre en nombre fractionnaire. Il suffit pour cela de retirer au numérateur la quantité du dénominateur et garder ce qui reste pour la fraction. Ainsi, on a 17/12 = (12+5)/12 = 12/12 + 5/12 = 1 5/12.
Publicité
Méthode 3
Méthode 3 sur 4:Additionner et soustraire des nombres fractionnaires et des fractions impropres
-
1Transformez les nombres fractionnaires en fractions impropres. Un nombre fractionnaire se présente sous la forme d'un entier suivi d'une fraction, le tout constituant une seule et même valeur (Ex. : 1 5/12). Par fraction impropre, on entend une fraction dont le numérateur (nombre du haut) est supérieur au dénominateur (nombre du bas). On a vu précédemment 17/12, fraction impropre s'il en est.
- Pour illustrer notre propos, nous prendrons 13/12 et 17/8.
-
2Trouvez le plus petit dénominateur commun aux deux fractions. Nous vous rappelons qu'il y a trois façons de procéder : avec les multiples, avec les facteurs premiers et en multipliant les dénominateurs.
- Dressons la liste des multiples de 12 et 8. Pour 8, on a, 16, 24, 36… Pour 12, on a 12, 24, 36. Le plus petit commun multiple est 24.
-
3Multipliez maintenant les numérateurs et les dénominateurs, pour que ces derniers soient identiques et les fractions inchangées. Les deux dénominateurs doivent être égaux à 24, le PPCM. On multiplie 12 par 2, et 8 par 3. Maintenant, comme on a multiplié les dénominateurs, il faut faire de même avec les numérateurs, et dans les mêmes quantités.
- On obtient ainsi : (13 x 2)/(12 x 2) = 26/24 et (17 x 3)/(8 x 3) = 51/24. On n'est pas loin de notre solution !
-
4Additionnez (ou soustrayez) vos fractions. Maintenant qu'elles ont été réduites au même dénominateur, on peut les additionner ou les soustraire sans trop de difficultés. On additionne ou soustrait les numérateurs et on laisse le dénominateur inchangé.
- 26/24 + 51/24 = 77/24. Voilà votre réponse, mais le numérateur semble bien gros comparativement au dénominateur, non ?
-
5Transformez votre réponse (fraction impropre) en nombre fractionnaire. Il est difficile de se rendre compte de la valeur de cette fraction. On va retirer autant que possible du numérateur la valeur du dénominateur, et quand l'opération ne sera plus possible, on conservera le reste de la soustraction.
- Combien y a-t-il de fois 24 dans 77 ? Réponse : 3 fois (3 x 14 = 72) et il reste 5 (72 + 5 = 77). Donc 77/24 = 3 5/24. Problème résolu !
Publicité
Méthode 4
Méthode 4 sur 4:Additionner ou soustraire des fractions sans regarder le PPDC
-
1Listez les fractions.
- Par exemple : ½ + ¾ + ⅝
-
2Commencez par résoudre les numérateurs.
- Dans cet exemple, multipliez 1 par le dénominateur des autres fractions.
- Multipliez donc 1 par 4 puis 8, ce qui donne 32.
-
3Procédez de la même manière pour les autres fractions.
- Multipliez 3 par 2 puis 8, ce qui donne 48.
- Multipliez enfin 5 par 4 puis 2, ce qui donne 40.
-
4Additionnez les résultats.
- 32 + 48 + 40 = 120.
-
5Vous avez maintenant votre numérateur.
-
6Cherchez le dénominateur.
-
7Multipliez tous les dénominateurs.
- Dans cet exemple : 2 * 4 * 8 = 64.
-
8Vous avez la réponse !
- 120/64 = 1 56/64 = 1 ⅞ !
Publicité